
Pedal Triangles
by Michael Walliser
Suppose we are given a triangle ABC and an arbitrary point P in the plane. Let us then construct perpendiculars from P to each side of triangle ABC (or extension of a side, if necessary), where the intersections of these perpendiculars with the sides are points R, S, and T. Triangle RST is called the Pedal Triangle for Pedal Point P. Examples are shown below with the pedal point inside and outside the triangle, respectively.
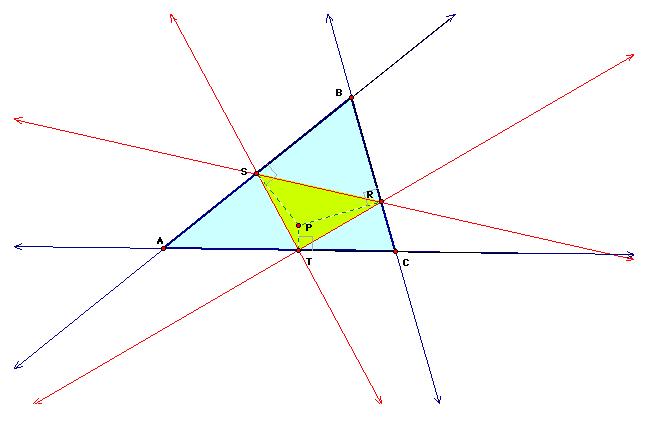
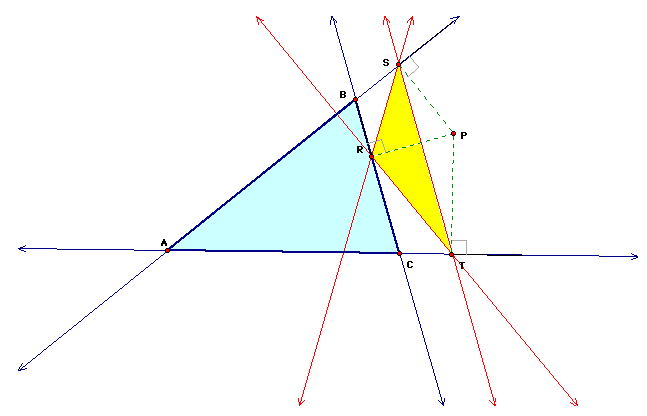
Click here to open a GSP file with a script tool that creates a pedal triangle given three points of a triangle and a pedal point.
Recall that the orthocenter lies on the intersection of the three lines that run perpendicular through each side and its opposite vertex. These perpendicular intersections form the orthic triangle. Notice that the pedal triangle is constructed in a similar manner, but instead of running perpendicular lines through the opposite vertices, we run them through a single, arbitrary pedal point. Therefore, if we place the pedal point at the orthocenter, the pedal triangle is the same as the orthic triangle. The GSP file linked above also contains tools that create the orthocenter and orthic triangle, so you can try it out for yourself. Note that the concurrence of the triangles holds even in an obtuse triangle, where the orthocenter (and therefore pedal point) is outside the triangle.
Now let's examine what happens when we place the pedal point at the circumcenter of the triangle. Recall that the circumcenter is equidistant from all three points of a triangle. Therefore, any two vertices and the circumcenter form an isosceles triangle, with the base being the side that also lies on the original triangle. We know that for any isosceles triangle, the perpendicular bisector of the base runs through the opposite vertex. If we reverse that process by starting at the circumcenter dropping a line perpendicular to a side, it will bisect that side segment. We see this for demonstrated for triangle JKL below.
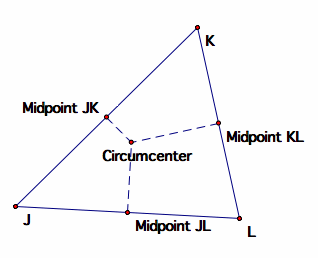
Remember how to construct the pedal triangle given a pedal point. First we drop perpendicular lines from the pedal point to each side, then we connect the intersections of these perpendiculars and their corresponding sides (or extensions). If we place the pedal point at the circumcenter, the vertices of the pedal triangle are just the midpoints of the sides of the original triangle. In other words, the pedal triangle is the same as the medial triangle.
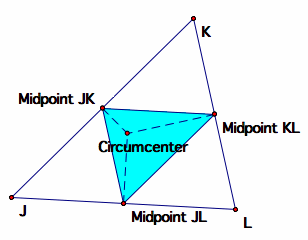
The GSP file linked above also has script tools for circumcenter and medial triangle, so experiment on your own. Notice that the construction holds for obtuse triangles as well.