Assignment 2

Jonathan Beal -

Perplexing Parabolas

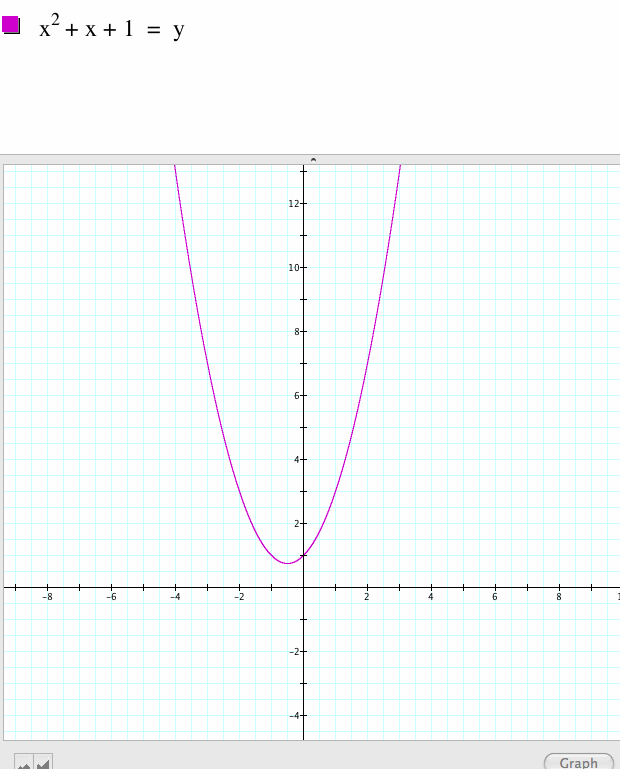
In this exercise, I am going to explore and play with quadratic equations.

Specifically, y = ax^2+bx+c.

I can graph parabolas of different shapes and sizes by changing the values of the coefficients.

First I want to look at the terms of the function individually.

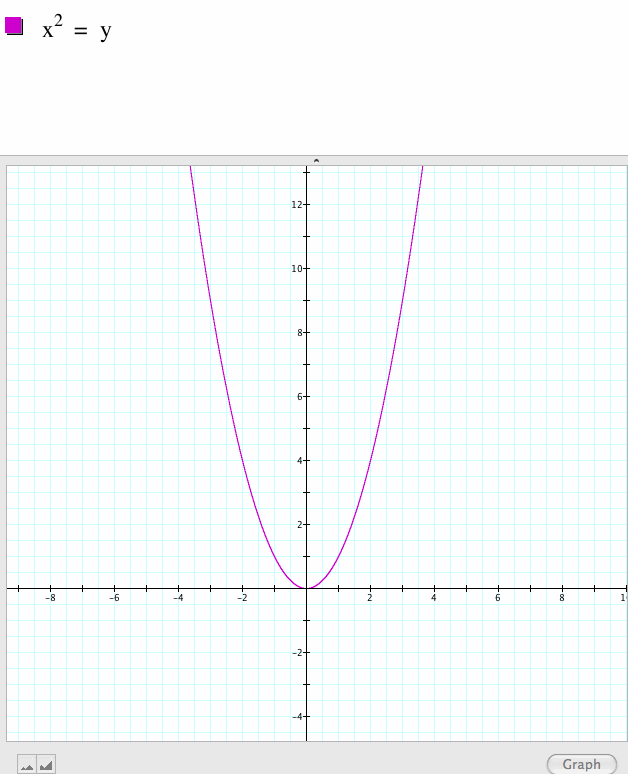When we build from here, we see the function centered at the origin. The function is symmetrical across the y- axis. If the first term were negative, the parabola would open downward beneath the x-axis.

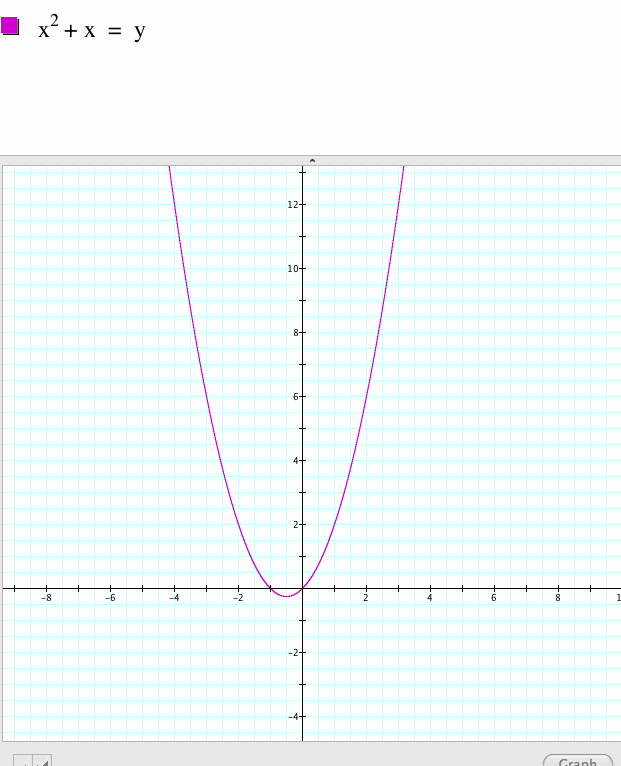Now the parabola is moved to the left of the y-axis. The function has roots of -1 and 0.

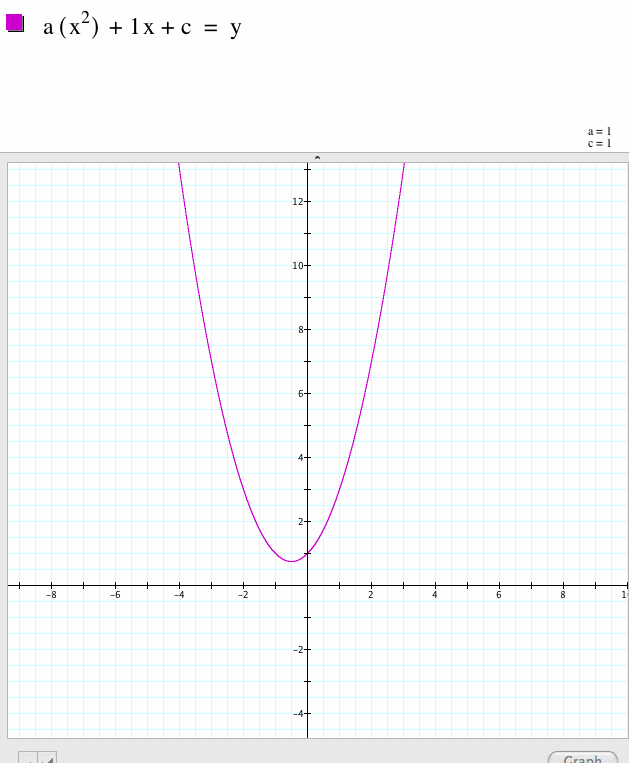
For the third term for the equation, ax^2+bX+c, I am going to let c=1 to demonstrate how the function moves in a positive direction up the y-axis.
	Notice, the function has no roots in this case.

Now I want to explore what manipulating each term does to the function and how this affects the other variables.

First I will look at examples of the first term.

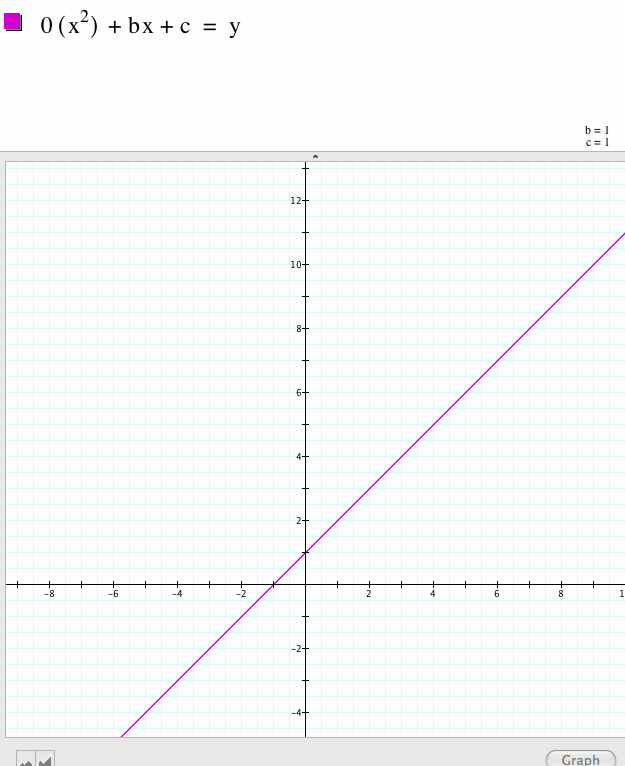	Without the first term, the function devolves to a line going through 1 at each axis.
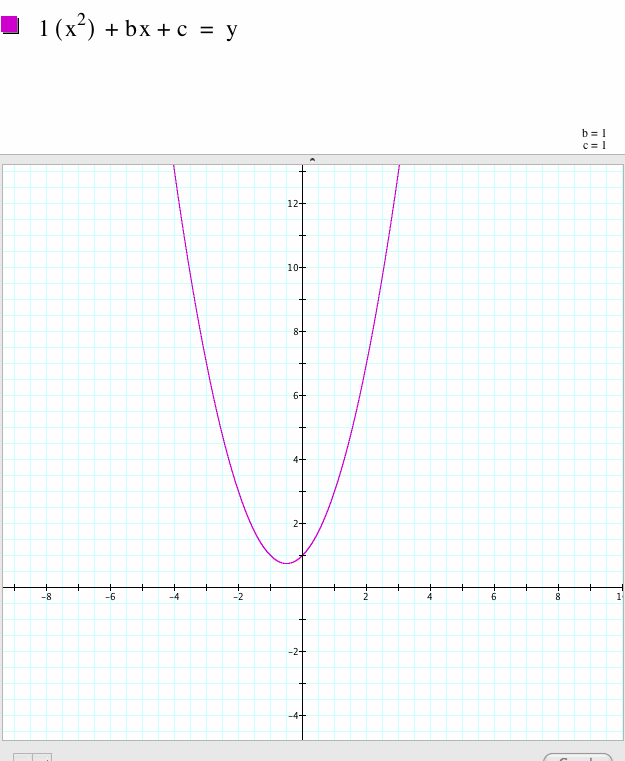	Look and see, when the coefficient in the first term is 1, then the graph is centered at .5 and it has no roots.
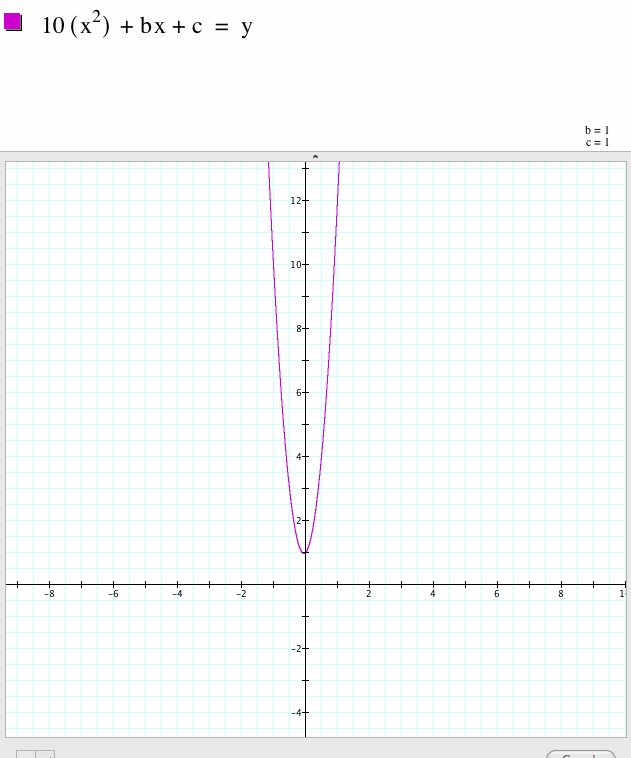	Now, we begin to see the characteristics of the value of the first term. The area between the legs of the parabola are coming closer together
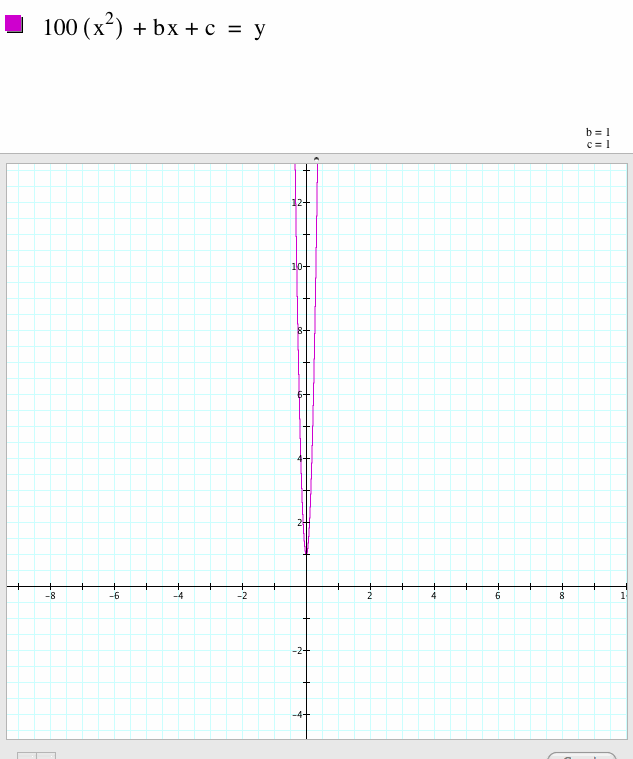	And the parabola has closed up a lot with a big increase in the value of the coefficient. It almost has formed a line on top of the y-axis.

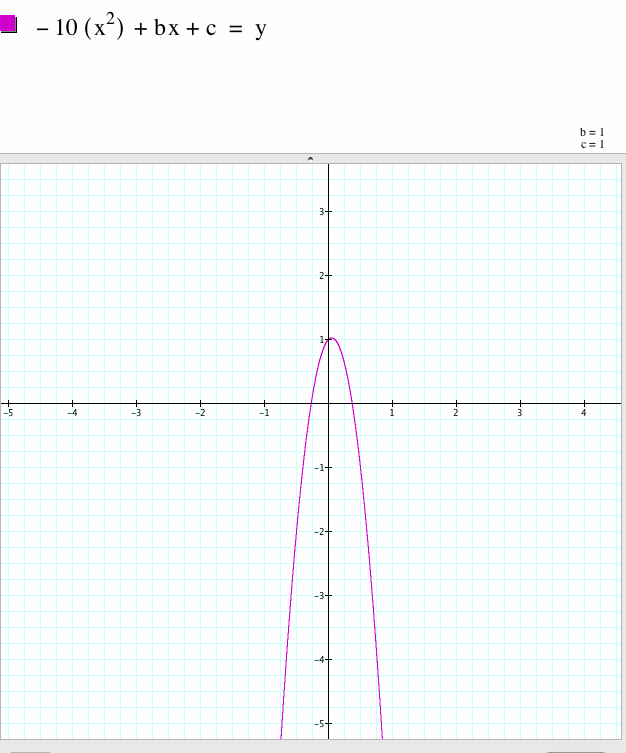And to turn the parabola upside down, the leading coefficient needs to be negative. To turn the parabola to the side, this requires a different function: ay^2+by+c=x

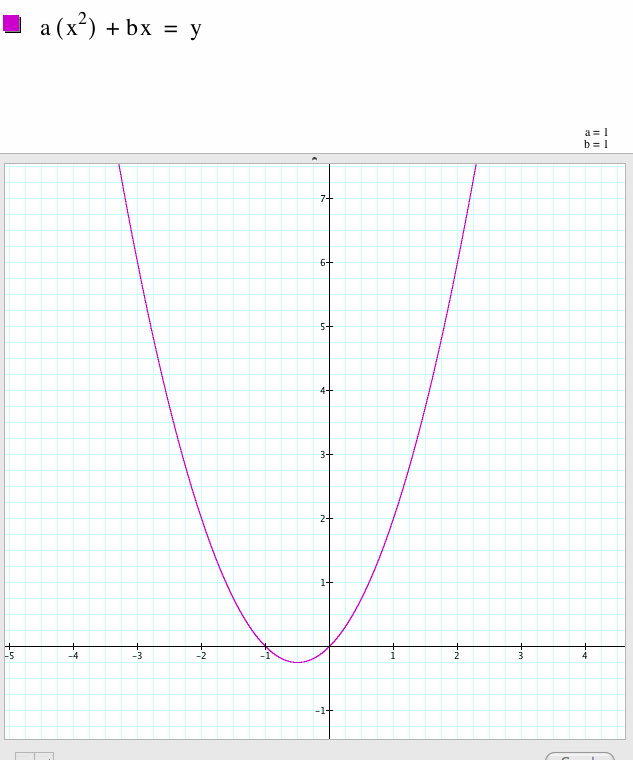
Next, I will focus on the properties of the coefficient of the second term.

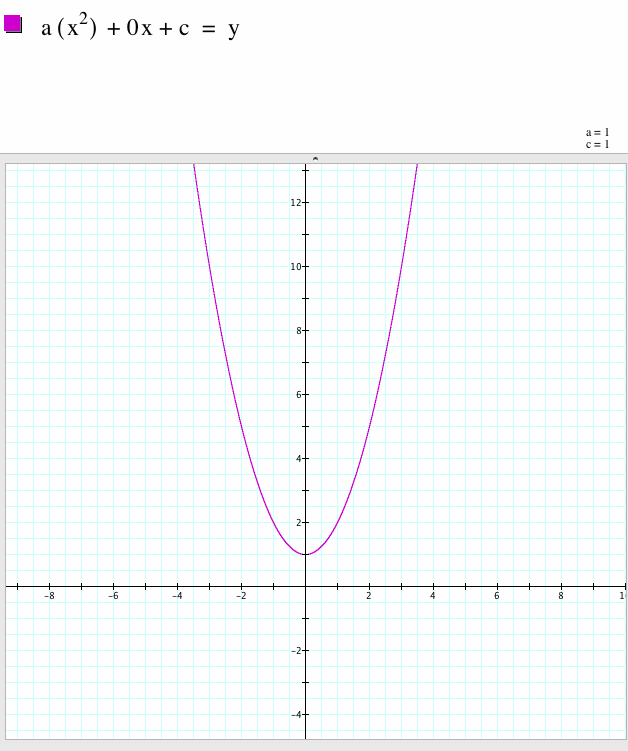	The coefficient is 0 in this function as a control example. Without the second term influencing the equation, the parabola is centered on the y-axis. The trough of the function is at 1.
	In this example, which we have seen a couple of times now, the parabola moves to the left by .5.
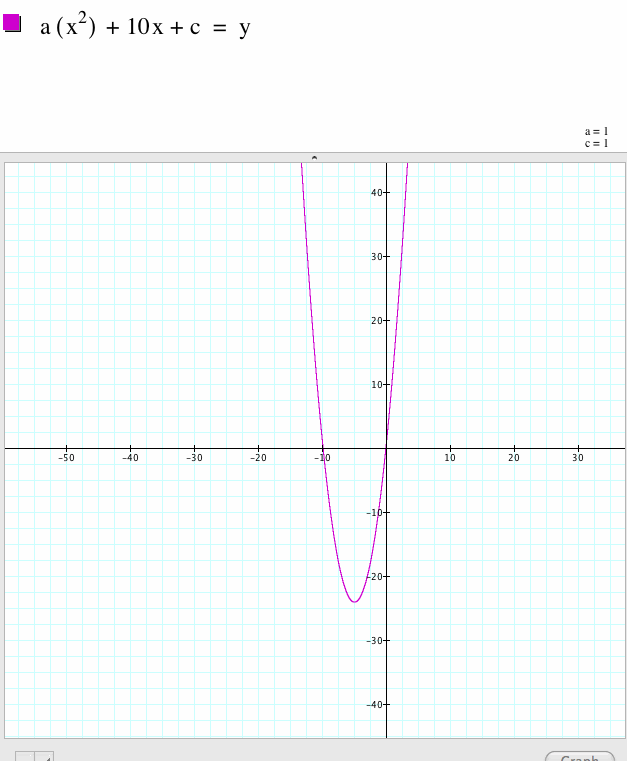	I can see that the values of the second term stimulate the parabola to extend downward.
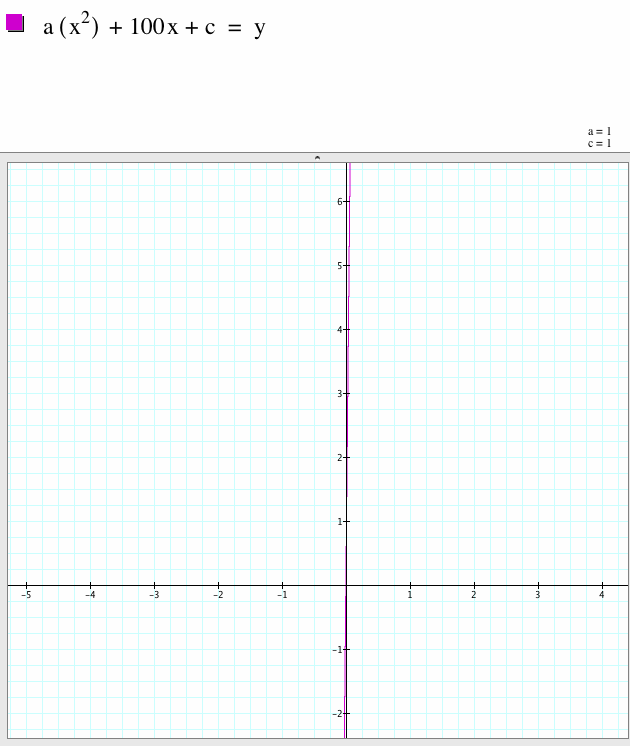
	These two graphs are the same. The one on the right is not showing fully everything going on. When I expanded the graph, I could see the whole function more clearly.   Look how far down the x-axis the function goes when the coefficient is 100.

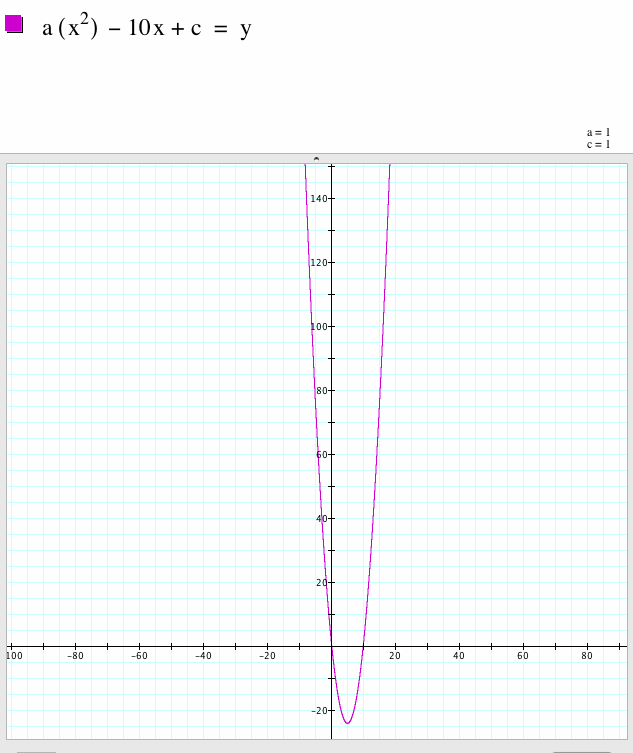
When we make the second term negative, the parabola is no longer on the left side of the y-axis but has moved to a mirror image on the right side.

And now we are going to play with the third term in the equation. In ax^2+bx+c, c is the constant. It should not have any effect on the function other than the position on the graph.

Let C=n

When c = 0, the graph has roots at -1 and 0. This variable will make the function move up and down. Watch and be amazed!

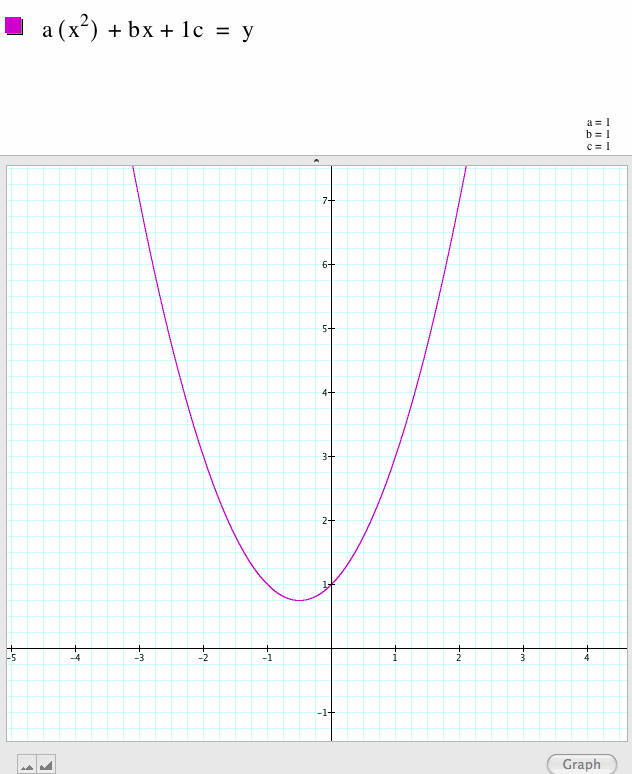See. The function has moved up when c=1. The rest of the function has not changed. It is not wider or more narrow. Will this continue as the number get larger?

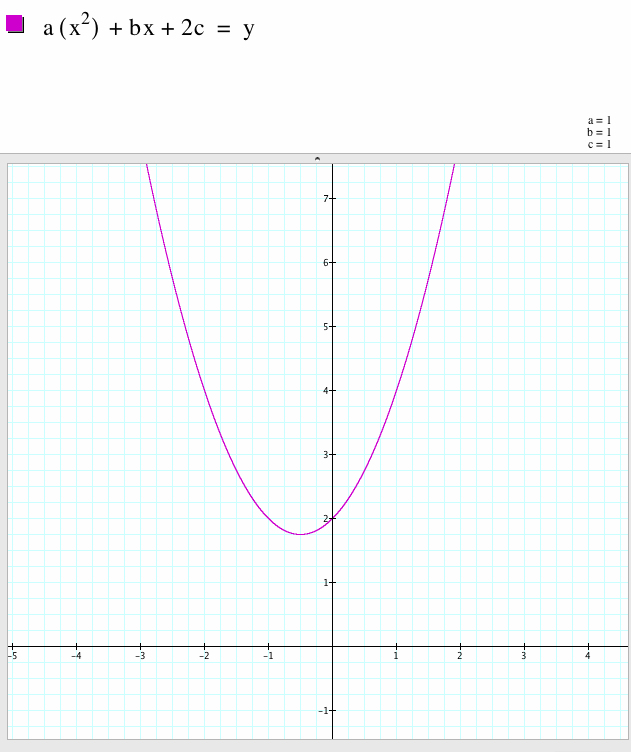In this equation, c=1 and the coefficient is 2. The function moved upward on the y-axis as it did when previously. This trend will continue as c gets larger and larger. We could expect then that if the numbers were negative that the graph would decrease in altitude as they got smaller and smaller.

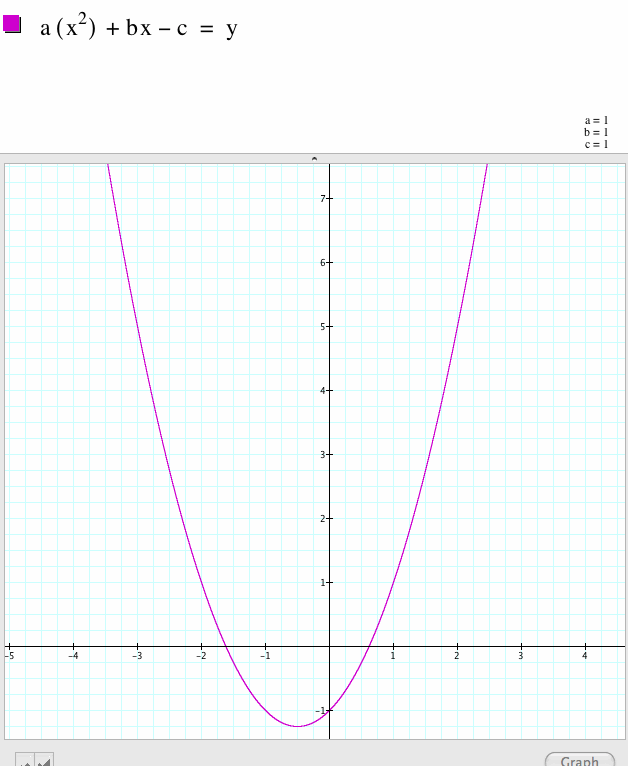As I expected, the parabola's minimum or trough sunk when c = -1.

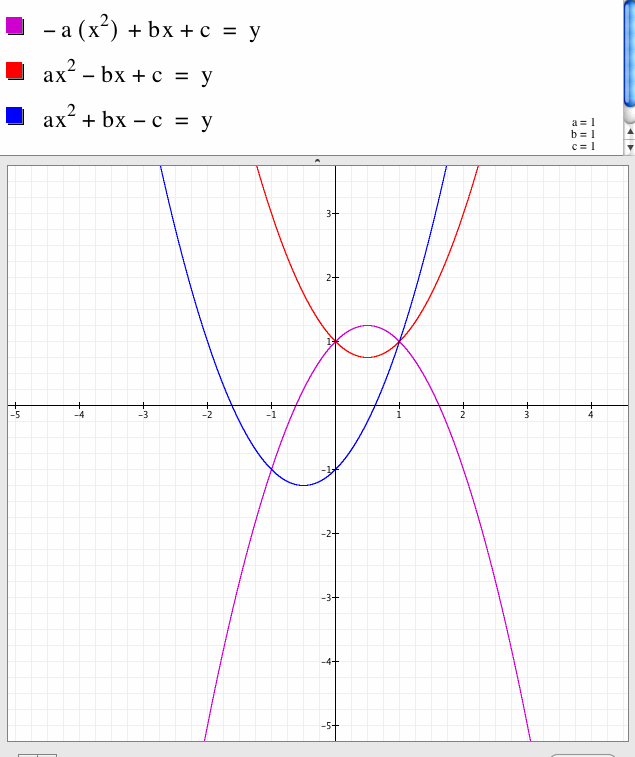
Let's see what happens if we explore all variable movements at the same time.

First I show the negative effects of each term on the function.

Next, I show the movement of all the variables. We can see all the previous steps by each variable all at once and how each respective variable compares with another variables

Back to Home Page