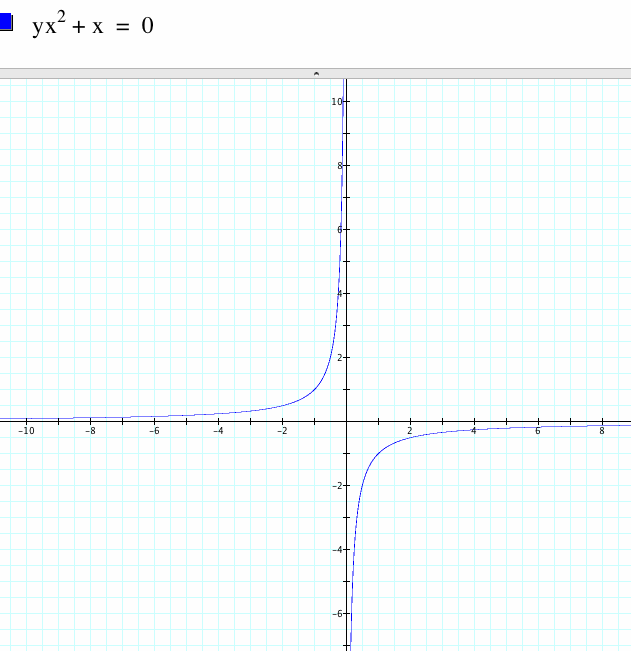
This function creates a hyperbola that has a point of discontinuity when x=0. Since we are working on the xa plane, and looking at the graph we can see that there are infinite roots of the function.
Assignment 3
Jonathan Beal -XA Plane
Here's a math joke for you.
| A very large mathematical convention was held in Las Vegas. The conventioneers filled two hotels, each with an infinite number of rooms.The hotels were across the street from each other and were owned by brothers. One evening, while everyone was out at a bar-b-que, one of the hotels burned to the ground. The brothers got together and worked out a plan. In the remaining hotel, they moved all guests to twice their room number -- room 101 moved to 202, room 1234 moved to room 2468, etc. Then all the odd number rooms were empty, and there were an infinite number of odd rooms. So the guests from the other hotel moved into them. |
In this exploration, I am going to looking at the xa plane with the function ax^2+x+1. I will look at the shape of the function, where are its roots, and anything else that looks worthy to write about.
First, as a background, I thought it would be necessary to look at the function ax^2+x=0 to gain some insight to the function and its graph.
Whenever you see a Y on the graph, this is really a A, because we are looking at the xa-plane.
 |
This function creates a hyperbola that has a point of discontinuity when x=0. Since we are working on the xa plane, and looking at the graph we can see that there are infinite roots of the function.
|
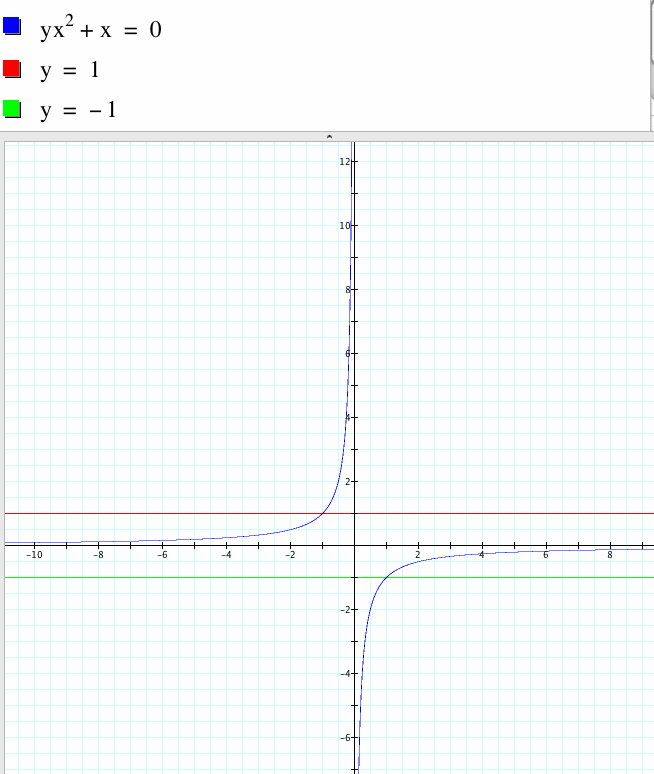 |
Notice that any horizontal line on the plane is an intercept. When the horizontal line on the a -axis moves to 0 then the function is undefined at this point. |
Now if we add one to the function we will get different results. This is the graph of ax^2+x+1=0.
| In contrast to the previous equation, when A is greater than approximately .25, then the function does not have roots. Next, when a < .25 the function has infinite roots. The horizontal line could move all the way down the a-axis to map all the roots. |
Let's explore a bit more with this problem.
First I want to compare the graphs of ax^2+x+1=0 and ax^2+x-1=0.
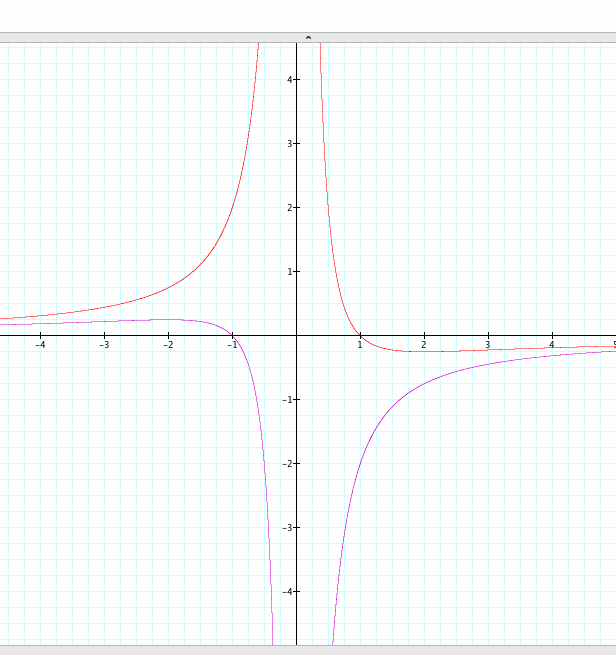 |
Notice how we almost have the original hyperbola. The +1 or -1 cause a side of the regular shape to reflect across a=1 to produce the deformed hyperbola. These two functions together have infinite roots but are still undefined when x=0. |
Now I want to see the range of the movement of the these graphs together. With the range set at -10 and 10 we should see the both functions converging to 0 and closing the gap in the discontinuity.