Assignment 6
Picture, Picture, on the Wall: What's the Best Angle to See You All?
Jonathan Beal
There is a 4x4 picture in my living room that hangs over one of the doors in my house. It is about 2 feet above my eye level.
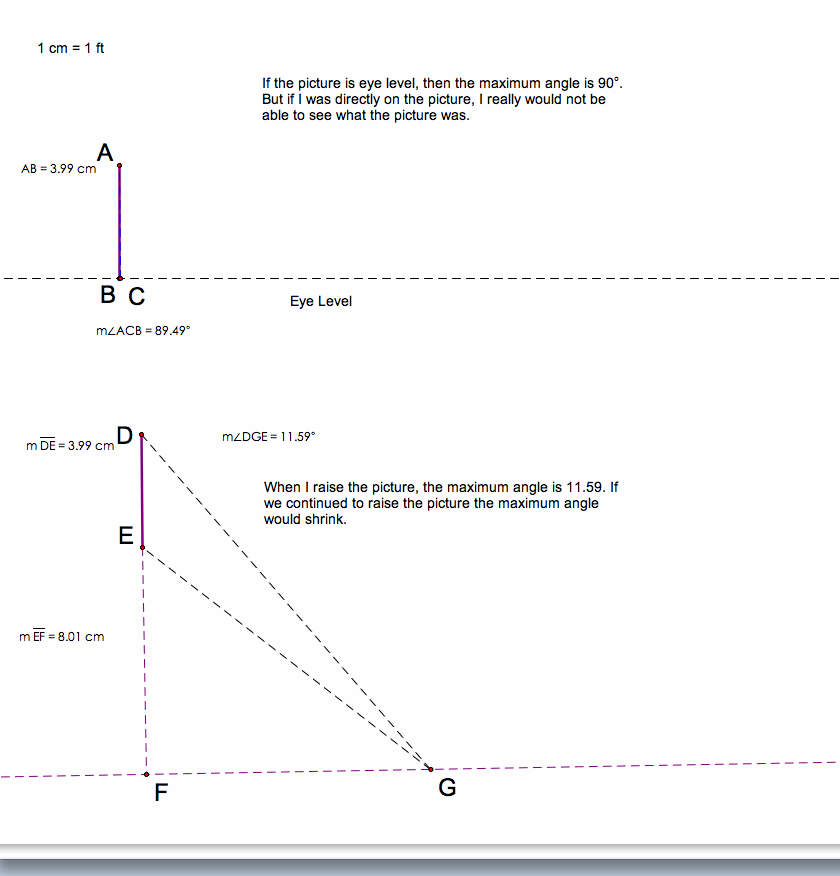
I stare at it everyday and think that it is unusual that the picture is above the door. How can you fully see a picture if it isn't eye level? Aesthetically, this picture didn't fit right there. So I got the idea to take some string and find the best spot to stand to find the greatest angle to see the picture. I nailed some string to the top and to the bottom of the picture. Then, starting from close to the picture, I measured the angle and worked my way backwards.
This is an illustration of what I got.

Notice a few things in the diagram, please.
1. <AEC = 12 degrees (or approximately 12 degrees) and <ADC = 12 degrees
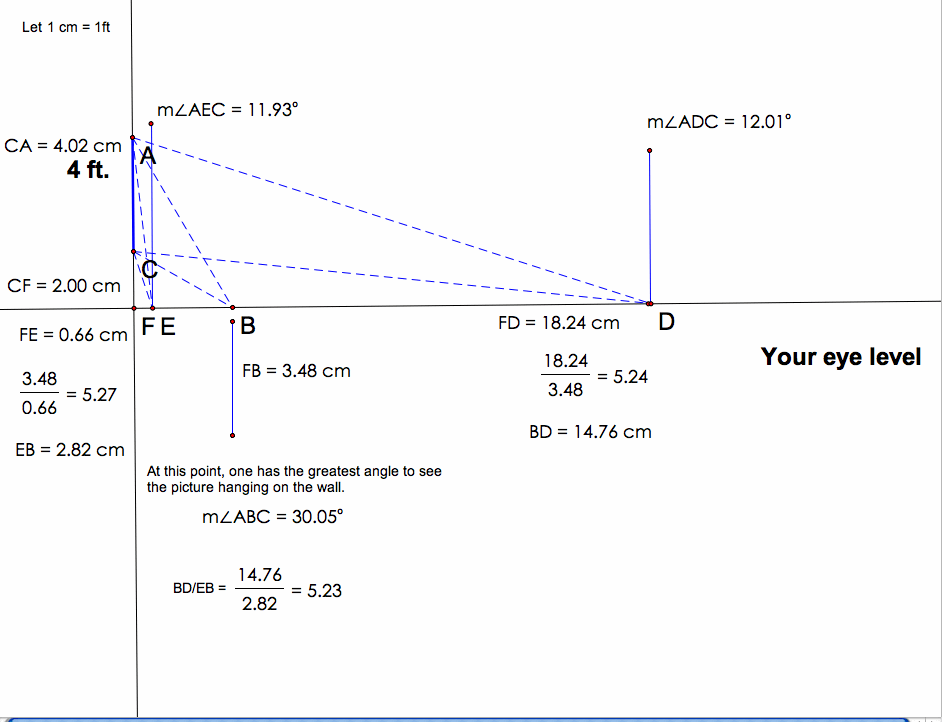
2. The distance Point F to Point B is 3.48 ft. Point B is the is the spot where I find the maximum angle to look at the picture.
3. Point E is .66 ft and Point D is 18.24 ft., yet both are vertexes to angles with the same measurement.
4. The distance ratio of E to B is equal to the distance ratio of B from D. E/B = 1/5.24 = B/D
5. EB = 2.82 and BD = 14.76 and EB/BD = 14.76/2.82 = 5.23.
After I finished measuring this picture, I felt as if I needed to explore more.
I took my trusty string and and went to measure other pictures in the house to see if they shared the same attributes as the first picture.
Would other objects have the same ratio as far as the distance was concerned? Would moving the picture up and down effect the maximum angle?
I had to know.
Here are some samples of how I changed the parameters.
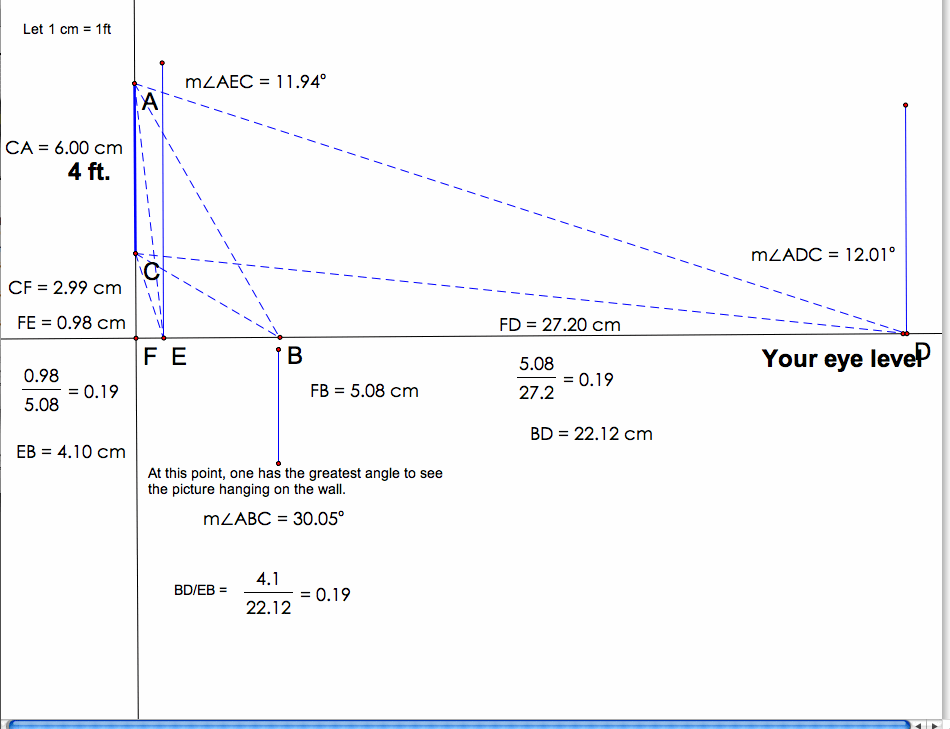 |
In this diagram, I increased the height and kept the ratio of 2:1 between eye level to the bottom of the picture and the bottom of the picture to the top of the picture. The top of the picture is now at 6 ft and the bottom at 3ft. Even though the picture was made larger, the ratios between the distances did not change. The angles did not change either.
Let's see what happens when I change the ratio of the picture. If I make the height of the picture .5 the distance from the eye level, I think the angles will change but the ratio of approximately 1/5 will remain the same. |
 |
I had to change the variables of the picture so that visibility of the diagram would be easier for anyone examining this. The maximum angle did change and my outer angles that I use to compare are also different. Given there is some precision missing, the ratios in the distances are the same are again approximately .2. I changed the size of the picture to 1ft and the distance from eye level to the bottom remains 2ft. I also kept the ratio of the angles constant. So what if I change the ratio of the angles. Instead of my outer angles being 2/5 of the maximum angle, why don't I make them 1/5. Will this change the ratio in the distance?
|

When I changed the other angles to 1/5 of the maximum angle, the distance ratio changed also to 1/5. What is this distribution? For my last investigation, i want to see what happens when I move the picture up and down.