Assignment 7

Jonathan Beal

And Around, Around We GO!

 

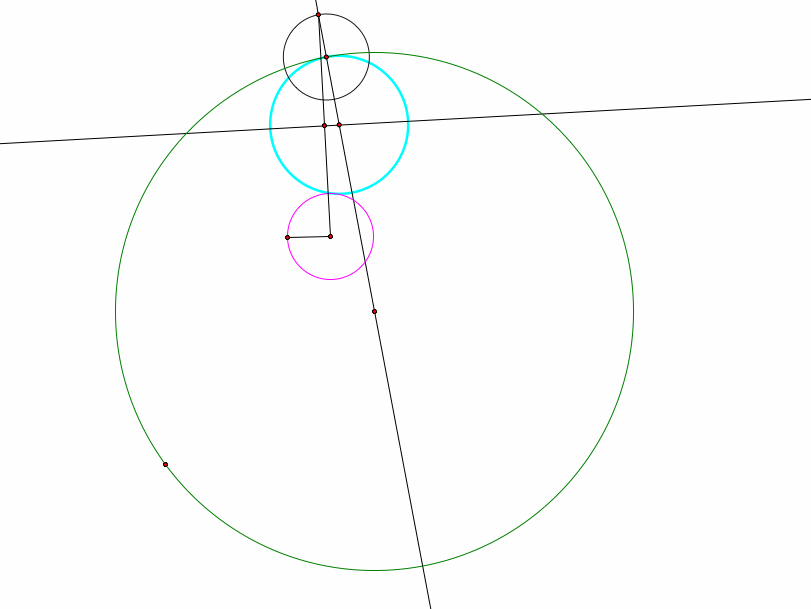
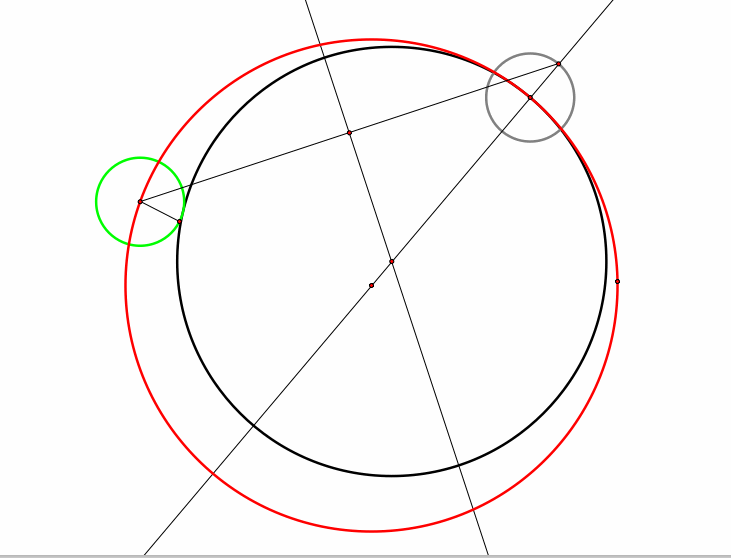
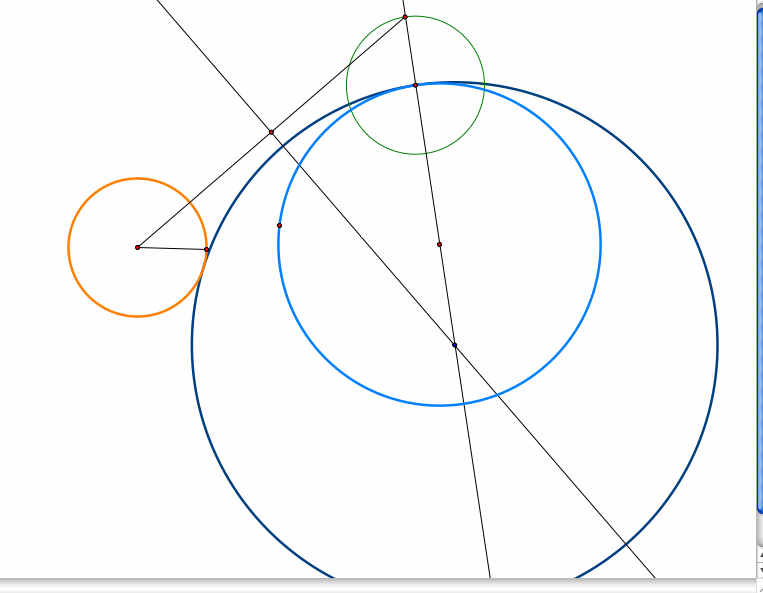
In this study, I am exploring circles and tangent lines. I am given two circles, one large green one and a smaller pink circle inside the larger one. I am to find another circle (the blue circle) that is tangent to them both.

I am going to show three different scenarios where I find the tangent circle.

1) One circle is inside the other one

2) One circle is intersecting another circle

3) One circle is outside and away from the other circle

 

1) On the right is the first example of finding the tangent circle. To see the animation go to the GSP file and play around with it. Watch how the center of the construct circle forms an ellipse as the point rotates around the larger circle.

 

 

 

 

In this exploration, I put one of the circles on to top of the other circle. See how the green circle intersects with the red circle. The black circle is the constructed tangent circle. How is it different from the previous example? The path that is traced goes through the neon green circle. Watch the animation of this example.
 

 

 

 

 

The circle on the outside dictates the size of tangent circle. The orange circle's distance from the blue circle makes the tangent circle bigger. Notice in this picture to the right compared with the other examples that the center of the tangent circle is lower than the center of the blue circle.

 

 
Also in this example, a hyperbola is traced, which is different from the ellipses that were created in the previous examples. Watch the GSP animation here.
if

Back to Home Page