Assignment 9

Jonathan Beal

When I Put P in the Center, Nobody Fusses.

 

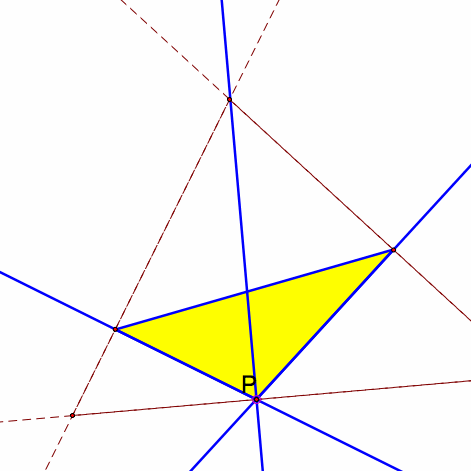
In this investigation, I am working with the pedal point and the pedal triangle. The pedal triangle is constructed by first choosing an arbitrary point in triangle ABC. Next, construct the perpendicular line of the point and a side. This creates the vertices of the inner triangle. The difference between a medial triangle and a pedal triangle is that a medial triangle connects at the midpoints of the sides to create the inner triangle. Also the orthocenter is different that the pedal point because even though they both are constructed by the using the perpendicular of the side, the orthocenter is made by the intersection of the three perpendicular lines rather than picking a point (or choosing the center) and the side to help create the perpendicular lines.

In the diagram to the right, this is a pedal triangle with the point P in the triangle. We can move the triangle around and the center of the triangle moves accordingly.

If you have GSP, you can go here and look at the triangle and move around the vertices, play with the center, and examine the results.

 

 

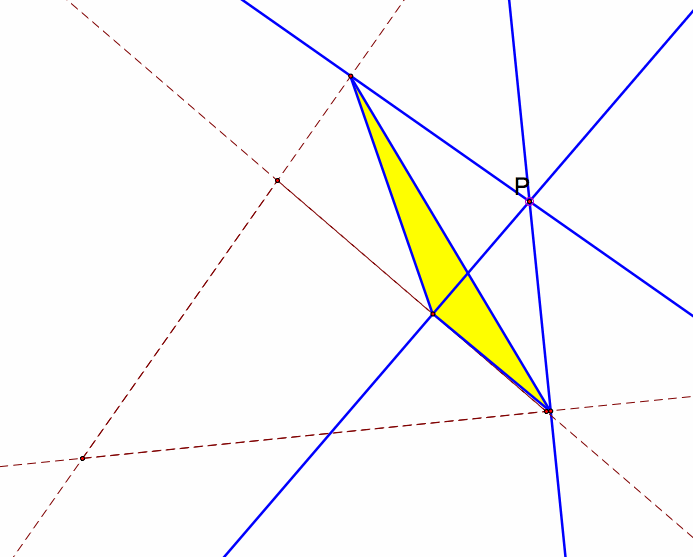
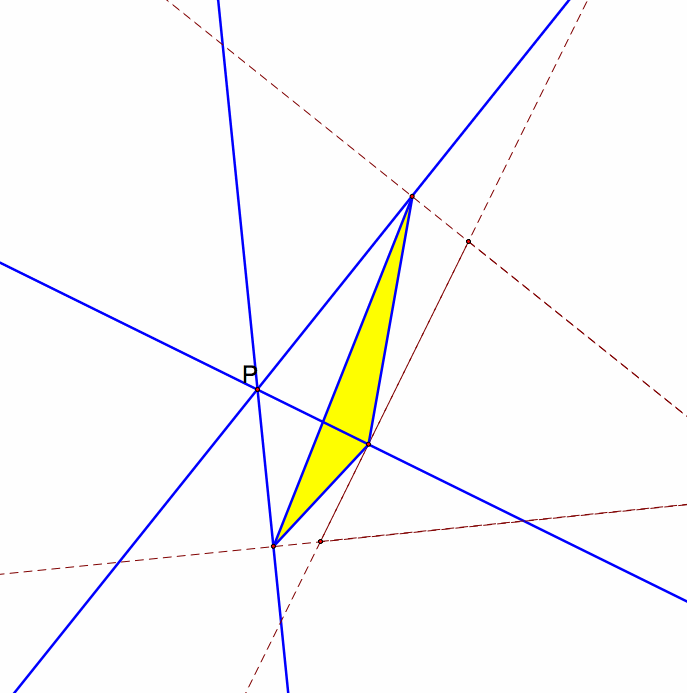
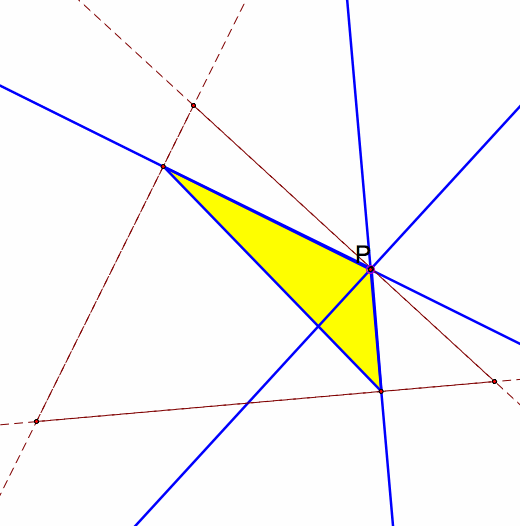
Here are some views of Point P outside the original triangle. I have included a couple of views around the triangle.

    
Notice how when the center P is moved outside of the original triangle that the pedal triangle becomes a obtuse triangle. This is because the vertices are following the edges of the original triangle. As the point is pulled out, the original triangle is extended and the edges are further and further apart.  

 

 

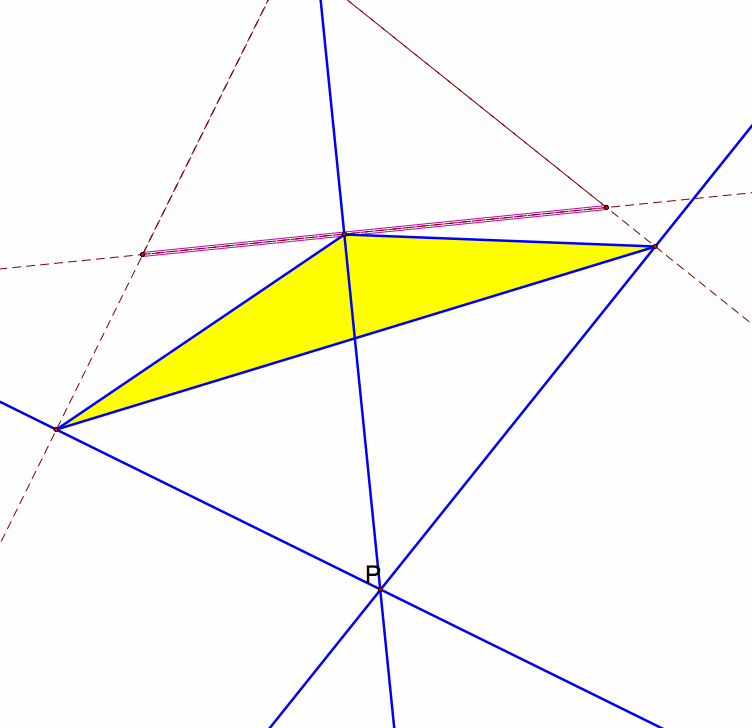
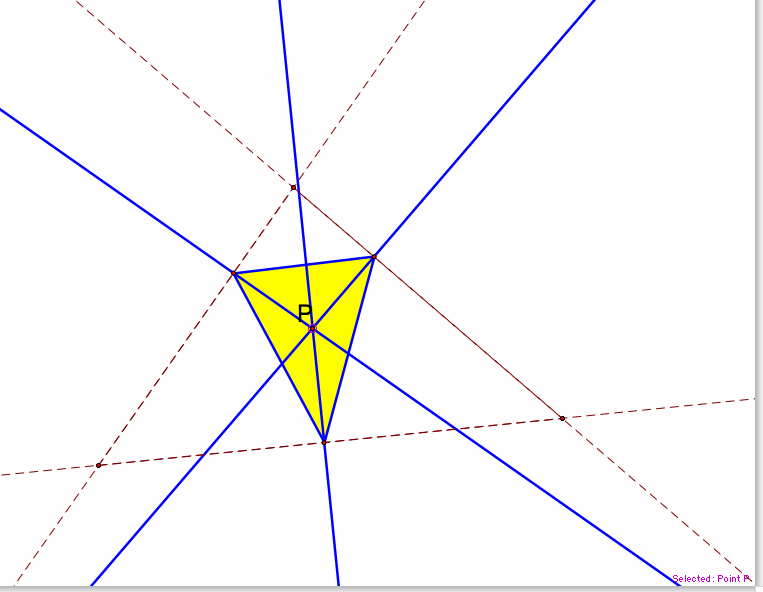
To explore a little bit deeper into this problem, what happens to the triangle if the point P is on the side of the triangle?

Normally, the pedal triangle is divided into three parts. When I move the pedal point to intersect with one of the lines on the triangle, the pedal triangle loses a partition.

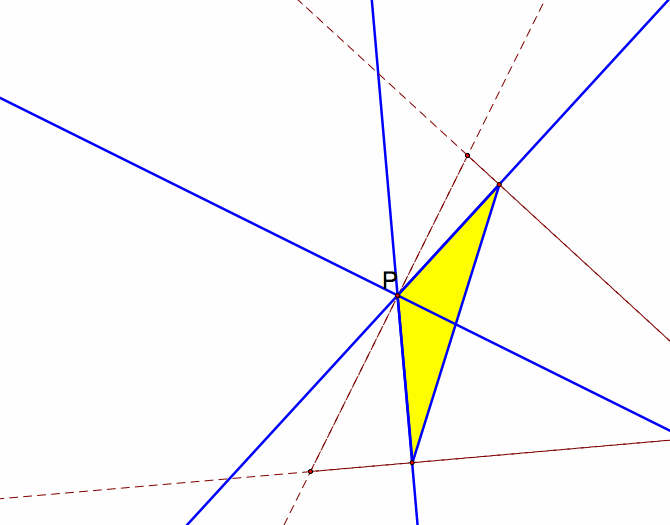
Notice, when the point P is closer to the midpoint that the altitude is greater than when P is closer to the any of the vertices.

Click here to go to the GSP drawing.

 

 

Finally, after playing with the pedal point on the edge of the bigger triangle, I wanted to see what happens when I put the pedal point at a vertex.

 

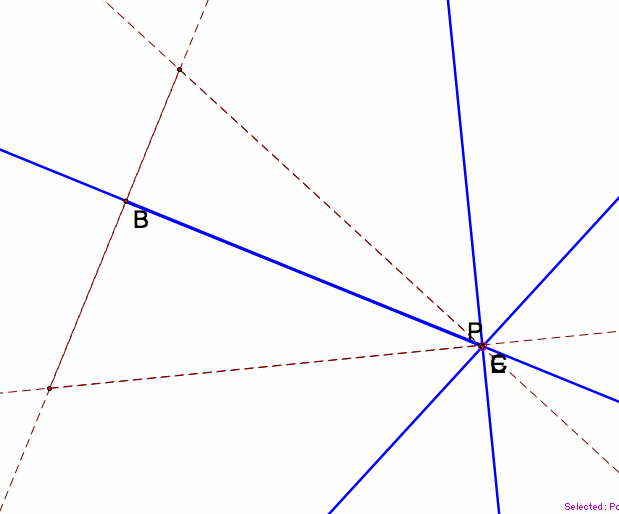
P at the vertex causes the pedal triangle to collapse. The result is that a perpendicular line from the vertex to the opposite side remains. The same conclusion will occur at each vertex.

Back to Home Page