Charlie Conway 7/27/2009
Parametric Equations
A parametric curve is represented by a pair of functions, x and y, and a parameter, t, such that x=f(t) and y=g(t).
In this exploration, we will discuss the case where f=cos and g=sin with t ranging from 0 to 2pi or 6.28319 rounded.
The graph for the original equation x=cos(t) and y=sin(t):
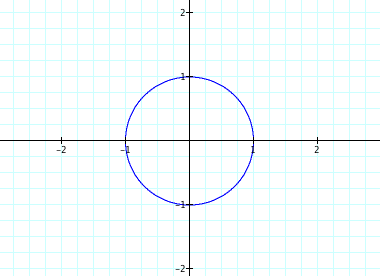
The graph is a circle with x-intercepts of 1 and -1 and y-intercepts of 1 and -1.
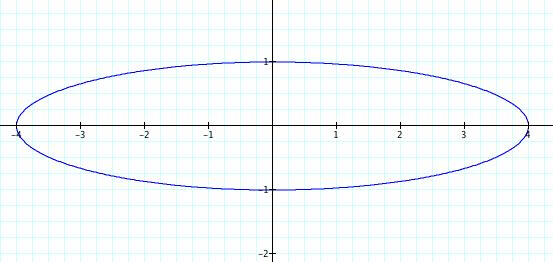
If we change the coefficient of cos(t) function, the graph become an oval, with y-intercepts still at 1 and -1 but with x-intercepts at the positive and negative values of the coefficient. For example, the following is the graph of x=4cos(t) and y=sin(t):
The exact opposite happens when we change the value of the coefficient of the sin(t) function. For x=cos(t) and y=4sin(t), the graph is
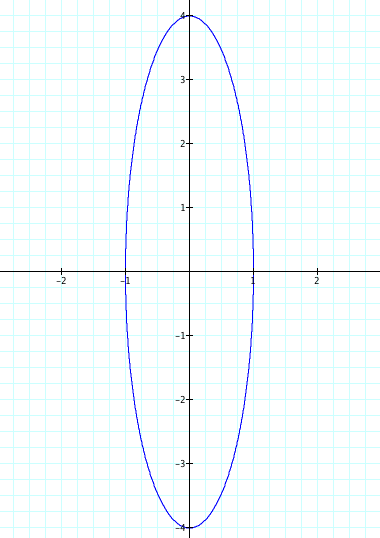
But what happens if we change both coefficients at the same time? As you might expect, the changes in the graph are independent of one another. A change in the coefficient of the cos(t) function results in the movement of the x-intercepts to the positive and negative values of that coefficient regardless of the coefficient of the coefficient of the sin(t) function. The same is true of the coefficient of the sin(t) function. Therefore, whenever the coefficients of cos(t) and sin(t) are equal, the graph is a circle crossing the x- and y-axes at the positive and negative values of that coefficient.
Now what happens if we change the coefficient of t? Let's begin by changing the coefficient of t only in the x equation.
As the coefficient of t moves, we have the following graph for x=cos(nt) and y=sin(t) (n ranges from -5 to 5).
This movie shows the graph beginning at n=-5, ranging up to n=5 in the middle, and back to n=-5 at the end.
As we have previously seen, when n=1, we have a circle. However, this is also the case when n=-1. In fact, it is true that additive inverses for the coefficient of t always give the same graph.
As you can see, changing n, the coefficient of t, drastically changes the shape of the graph. As |n| gets larger, the graph has more and more curves. However, not everything changes. The the x- and y-values still only range from -1 to 1, because we did not change the coefficients of the cos(t) or sin(t) functions.
A similar thing happens when we change the value of the coefficient of t in the y equation.
As the coefficient of t moves, we have the following graph for x=cos(t) and y=sin(nt) (n ranges from -5 to 5).
This movie shows the graph beginning at n=-5, ranging up to n=5 in the middle, and back to n=-5 at the end.
Again, when we have additive inverses for the coefficient of t, the graphs are the same. And again, the graph's values range from -1 to 1 in both the x- and y-directions. Also similar to the last graph, as |n| gets larger, the graph has more and more curves. The only difference is this time, the curves' maxima and minima are at y=1 and y=-1. Whereas, in the previous graph when we changed the coefficient of t in the x=cos(t) equation, the maxima and minima of the curves were x=1 and x=-1. Essentially, we have rotated the graph of x=cos(n) and y=sin(t)clockwise 90 degrees.