Charlie Conway 7/28/2009

SpreadSheet

If we begin with a 5x8 (in) sheet and want to cutout square corners to create a lidless box, how can we determine what size cutout gives the the maximum volume?

We can use a spreadsheet, such as Microsoft Excel to help decide the length of the cutout to maximize the volume of the box.

First we have to find the formula for volume.

Since the shorter side is 5 in. long, we obviously cannot cutout more than 5 in. However, we must realize that we are actually making two cuts of the same length on each side. Therefore, the length of one side of one cutout cannot exceed 5/2 or 2.5 in.

Also, we know that the formula for volume of a box is V=(l)(w)(h). In this case, when we fold the sides of the sheet up to make the box, the length of the cutout will also be the height (h). Let us call the shorter side the width (w). It can be represented as five minus twice the cutout, w=5-2(h). Similarly, the length can be written as eight minus twice the cutout or l=8-2(h). Thus the formula for the volume of the box is V = (8-2h)(5-2h)(h).

Now we can use Excel to quickly calculate the length, width, and volume of the box, given the height.

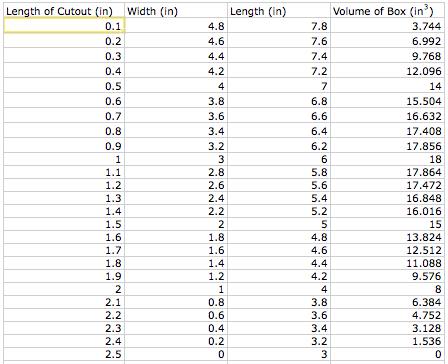
This only lacks a little bit of precision because I had to choose the increments of the cutout. Obviously, there is an infinite amount of different size cutouts we could make; however, I chose to increase by tenths of an inch to give a pretty good idea of the trends.

Excel can also display the results graphically, with Length of Cutout on the x-axis and Volume of Box on the y-axis.

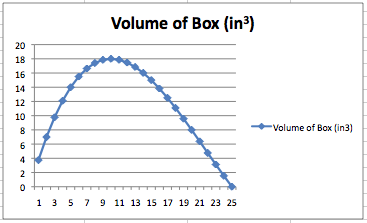
Excel plotted the given points and fit a curve to the data.

We can use calculus to verify Excel's results.

By taking the derivative with respect to x of our volume formula, we get

If we set this equal to zero and factor, we find that the maximum volume is made with a cutout size of 1.

And if we substitute 1 into our original equation, we see that the maximum volume of the box is 18.