First we begin with the graph of a standard parabola

y=2x^2+3x-1

 

Now we add the new graph

y=2x^2+3x-1+xy

The graph of the new function has two parts, and an asymptote appears at x=1.

The new graph has the same x- and y-intercepts as the original.

 

What happens as we change the coefficient of the xy term?

Investigate with this file.

As you will notice, as the coefficient of the xy term approaches 0, the lower curve moves toward negative infinity, while the upper curve turns to approach coinciding with the original parabola of y=2x^2+3x-1.

Also, as you will notice, the two parts of the new graph come close together as the coefficient of the xy term increases up to a certain point (between 3.5 and 3.6). Here the graph changes significantly. Instead of one part opening up and the other part opening down, with the majority of the upper part in the 2nd quadrant and the majority of the lower part in the fourth quadrant, the two parts seem to merge and begin to open to the left and the right. As the coefficient increases from this point, the two parts get sharper corners and begin to almost resemble the first and third quadrants (of course the asymptote remains at x=1).

When the coefficient of the xy term becomes negative (between the values of 0 and -0.5), the curves begin to turn clockwise around the origin, looking like they might resemble a reflection across the y-axis of the graph of the equation with the xy coefficient between 0 and 3.5. Then when the coefficient gets between -0.5 and -0.6, the two curves merge again and change from opening to the top and to the bottom to opening to the left and to the right.

As the xy coefficient decreases toward negative infinity, the graph is a reflection across the x-axis of the graph with positive xy coefficients. So the two curves get sharper corners and begin to resemble the second and fourth quadrants. The asymptote has also moved from x=1 to x=-1.

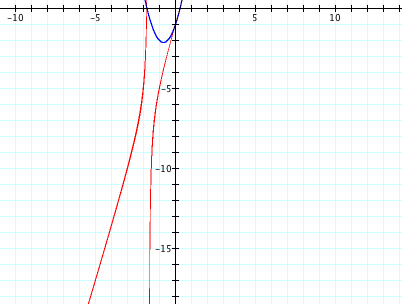
y=2x^2+3x-1-0.5xy and y=2x^2+3x-1-0.6xy