Charlie Conway 7/13/2009

Triangle From Medians

Task: Given three medians of a triangle, construct the triangle.

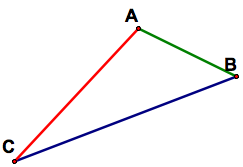
We begin with three line segments, which are the medians of some triangle. It might be useful to begin with these three segments as sides of a triangle.

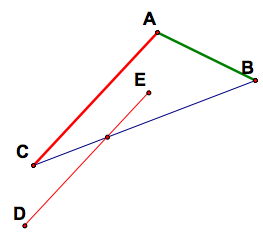
Now we need to construct the triangle for which these three segments are the three medians. We can start by using one of the segments (CB) for a median just as it is. Then we know that the centroid (the intersection of the medians) is located at a point on each segment, 2/3 from one endpoint and 1/3 from the other endpoint. In terms of the triangle, this would be 2/3 of the segment from the vertex and 1/3 from the midpoint of the opposite side. Thus, we must trisect CB, which gives us 2 intersection points for the other centroid. Obviously we only use one of these two points, but it is up to us to pick one. I will pick the lower.

The second median can be made by creating a parallel segment the same length as CA that intersects the lower of the two trisection point of the CB. However, the red median must also be trisected and must intersect the blue median so that the red segment is split into a 2/3 piece and a 1/3 piece. I will let the longer piece be below the blue median.

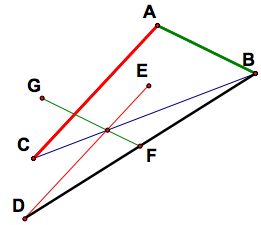
Now we must construct the green median but in a different fashion. First realize that the D and B are vertices of the triangle we are trying to construct. So the segment between these two point is one side of the triangle. Also, a median must intersect the midpoint of a side and go through the centroid. So we begin construction of the green median, GF, by finding the midpoint DE and constructing a segment the length of AB through the centroid.

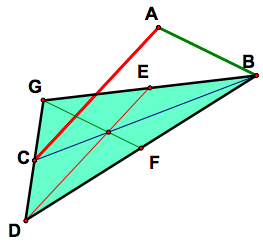
The length from G to the centroid is exactly twice as much as the length of F to the centroid. Therefore, GF is a median, and G is the third vertex of the triangle. Thus, the triangle with medians the lengths of CA, CB, and AB is DGB.