Charlie Conway 7/16/2009
Tangent Circles
Task: Beginning with two circles, X and Y, and a point on Y, construct a circle tangent to both given circles going through the given point. Also discuss the locus of the given point of tangency on the circle and the center of the new circle.
To construct a circle tangent to two circles, X and Y, through a point, A, on Y, we must find the center of the new circle. To do this we use an isosceles triangle. The length of the two equal sides of the isosceles triangle will be the sum of the radius of one of the given circles, X, and the radius of the circle we are constructing. Although we don't know where the center of the new circle will be, it must lie on the radius of the other given circle, Y, to the point A. If we extend this radius by the length of the radius of X and call this point B, we then can connect B and the center of X, forming the base of the isosceles triangle. The perpendicular bisector of the base of an isosceles triangle intersects the opposite vertex, which will be the center of our new circle. Therefore, the intersection of the perpendicular bisector of the base of the triangle and the radius XA gives the center of the circle tangent to our two given circles.
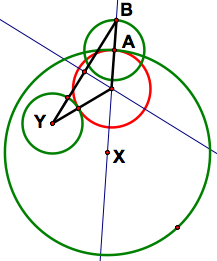
Now that we have constructed the circle tangent to two given circles, let us investigate the properties of this circle.
Click here for a workable GSP sketch of the situation.
Let us focus on the locus of the center of the newly formed tangent circle as the given point of tangency moves around its circle. There are three cases to explore:
Case 1: One given circle is completely inside of the other given circle.
When circle Y is inside circle X (or X inside of Y), the locus is an ellipse with the centers of X and Y as foci. This is the case everywhere except when the center of X and Y are concurrent. In this case, the locus is a circle, because the difference between the radius of circle X and the radius of circle Y is a constant. The absolute value of that difference is the diameter of the tangent circle. Since it remains constant, the locus of the center of the tangent circle and the given point of tangency is a circle.
Case 2: The two given circles intersect.
When circle X intersects circle Y, the locus of the center of the tangent circle and the given point of tangency remains an ellipse, but with a minor axis approaching zero. The locus reaches this point when the two given circles are tangent to one another and one is not inside the other. Since there is only one point of tangency in this case, there is only one circle that can be tangent to both given circles. It is a circle concurrent with circle X (the circle with the given point of tangency).
Case 3: The two given circles are disjoint.
When the two given circles move from tangent to disjoint, the locus of the center of the constructed tangent circle as the point of tangency moves around the circle becomes hyperbolic, again with the centers of the given circles for its foci. There are two points where the center of the tangent circle jumps from one piece of the hyperbola to the other. In terms of the tangent circle, this event occurs when the tangent circle gets exponentially bigger, approaching a straight line. This happens when only a straight line can be tangent to both of the given circles, with one circle on each side of the line.
Thus far, we have discussed the cases where the tangent circle is between the two given circles when one given circle is inside the other. However, there is another way of constructing a circle tangent to two given circles and a given point of tangency on one of the circles. In this second case, the tangent circle surrounds the given circle inside of the other given circle.
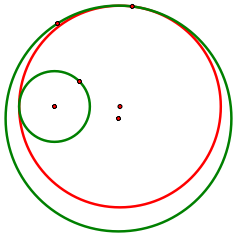
The construction is similar to the construction above; however, the radius of the smaller given circle must be subtracted instead of added, giving you the correct isosceles triangle to find the center of the tangent circle.
Click here for a working GSP sketch of this case of the construction.
Again, we will discuss the locus of the center of the tangent circle as the given point of tangency moves around the given circle.
Case 1: When one given circle is completely inside of the other given circle.
The locus of the center of the tangent circle and the given point of tangency is an ellipse. When the center of the two given circles become concurrent, the locus becomes a circle. As the inside given circle moves toward the edge of the outside given circle, the width of the elliptical locus gets smaller and smaller, approaching a line when the two circle become tangent to one another.
Case 2: The two given circles intersect.
An interesting fact about the tangent circle itself in this case is that when the given point of tangency is inside of the other given circle, the tangent circle is inside both given circles. But when one given circle intercepts the other in a place not surrounding the point of tangency, then the tangent circle is outside of both given circles.
When the two circles intersect, the locus of the center of the tangent circle and the given point of tangency becomes a hyperbola. Again, the center of the tangent circle jumps from one part of the hyperbola to the other when the tangent circle itself approaches a straight line. In this case, this occurs when a straight line tangent to both given circles can be drawn through the point of tangency.
Case 3: The two given circles are disjoint.
When the two given circles are disjoint, the locus is still hyperbolic. The center jumps from one piece of the hyperbola to the other again when a straight line can be drawn tangent to both circles through the given point of tangency. This occurs in two places, and it occurs when the tangent circle becomes that tangent line.