Soddy Circles
By: Krista Floer
First, a little history. Frederick Soddy was an English radiochemist and received the Nobel Prize for Chemistry in 1921. He was well-known in his field and even had a crater on the moon named after him. In 1936, he rediscovered Descartes’ theorem about 4 tangent circles and republished it as a poem. This poem is so interesting, that one must take a closer look.
Before looking at the poem, let us consider Descartes’ theorem:
If four mutually tangent circles have curvature ki (for i = 1,...,4), Descartes' theorem says:
![]()
Curvature is also called a bend. The curvature is k, and k is just the reciprocal of the radius, 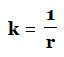 .
.
So we can rewrite the theorem like this:
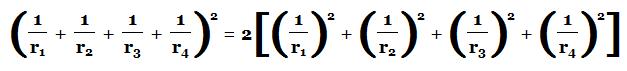
We have a great theorem, but there is no context to it. For many students of math, we do not see the importance of a theorem until we can see an application of the theorem. Let us then find a context for this theorem.
Consider the following problem:
Given three coins of possibly different sizes which are arranged so that each is tangent to the other two, find the coin which is tangent to the other three coins.
We can see that the coins form the context for the theorem.
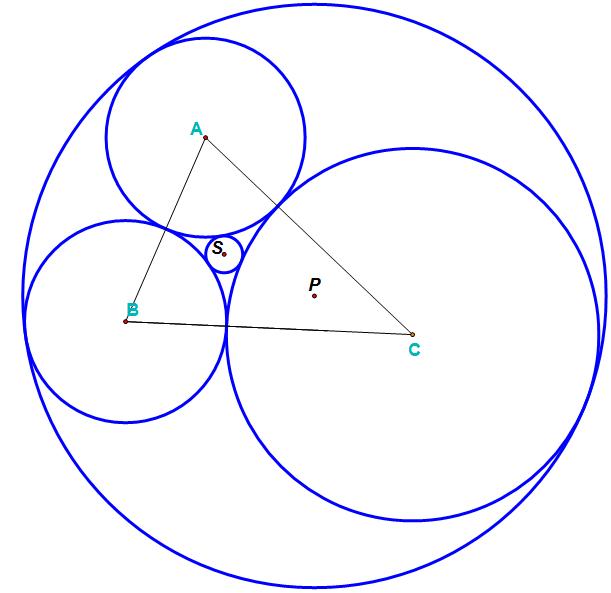
The construction of the picture of this problem interested me more than the formula. I wanted to know how to construct the circles so that one could see all 5 tangent circles at one time. In order to do this, we first have to construct the first three tangent circles that the inner and outer Soddy circles become tangent to.
For high school students, mainly those students in Math 1, I would want them to figure out a way to construct the 3 tangent circles; the three circles that would represent the three coins of possibly different sizes. All of the students should eventually be able to figure out the construction. They should present a true construction, not just a picture they drew with 3 circles that are mutually tangent. The construction the students come up with needs to work in every situation. The concept is not complicated. Have you figured out how to construct the three circles that are always tangent?
Constructing Basic 3 Tangent Circles:
The key is to first construct a triangle. Pick the three points that you want to be the centers of the three circles. These points will also be the vertices of the triangle. For this triangle, construct the incenter. (On my home page I have an assignment that constructs the incenter for you. I also provide instructions in the instructional unit for EMAT 6690.) From the incenter, construct a perpendicular line through the incenter to each of the sides. This is also how to construct the incircle. The intersection points of the perpendicular line to each side of the triangle is going to be the point where any two circles are tangent. We have now constructed the three tangent circles.

But how are the other two tangent circles constructed?
These circles are a little more complicated. Let’s first construct the outer Soddy circle:
Outer Soddy Circle:
Given triangle ABC,
Step 1: With AB as the smallest side, construct a point X on side AC so that AX = AB.
Step 2: Construct a point Y on side BC so that CY = CX.
Step 3: Construct the midpoint E of segment BY.
Step 4: Construct point D on side AB so that BD = BE.
Step 5: Construct a circle (circle a) with center A with radius length equal to AD.
Step 6: Construct a point U’ by constructing the perpendicular through A to BC. Where this perpendicular intersects circle a is the point U'. This point is the intersection point closest to side BC.
Step 7: Construct EU'. This segment intersects circle a at U.
Step 8: Construct the perpendicular AU'. Construct P' so that U'P' = AU'.
Step 9: P is intersection point of AU and EP'.
Step 10: Construct a circle centered at P with radius UP. This is the outer Soddy circle.
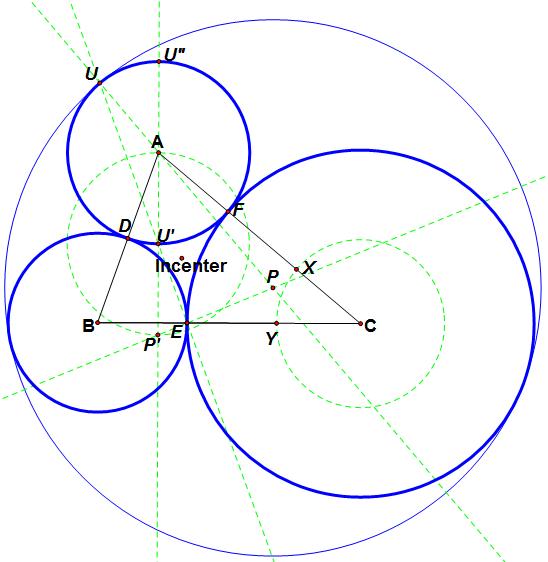
We started out with the requirement that side AB must be the smallest. AB does not have to be the side that you make the smallest, but for this construction to work it must be. If you want side BC to be the smallest, the construction can be altered by substituting the respective sides into the above instructions. If side AB is not the smallest, then at the point where is is not the smallest side, the outer soddy circle disappears.
This point P is called the Isoperimetric Point. Now how do we construct the other tangent circle? Keep reading…
Inner Soddy Circle:
Given triangle ABC,
Step 1: With AB as the smallest side, construct a point X on side AC so that AX = AB.
Step 2: Construct a point Y on side BC so that CY = CX.
Step 3: Construct the midpoint E of segment BY.
Step 4: Construct point D on side AB so that BD = BE.
Step 5: Construct a circle (circle a) with center A with radius length equal to AD.
Step 6: Construct a point U” by constructing the perpendicular through A to BC. Where this perpendicular intersects circle a is the point U”. This point is the intersection point farthest to side BC.
Step 7: Construct EU'. This segment intersects circle a at U.
Step 8: Construct the perpendicular AU'. Construct P' so that U'P' = AU'.
Step 9: Construct a circle centered at A with radius AP’. Point P” is the intersection of this circle and line AU’.
Step 10: Construct Point F as the point of tangency of circle B and C.
Step 11: Construct the perpendicular line through point B to side AC. The intersection of the perpendicular line and circle b farthest from side AC is point V”.
Step 12: Construct a circle with center V” and radius V”B. The intersection point of this circle and line V”B is point Q”.
Step 13: Construct line FQ” and line EP”. The intersection of these two lines is the center of the inner Soddy circle. Label that point S.
Step 14: Construct point R as the intersection of circle B and line FQ”.
Step 15 Construct a circle centered at S with radius RS. This is the inner Soddy circle.
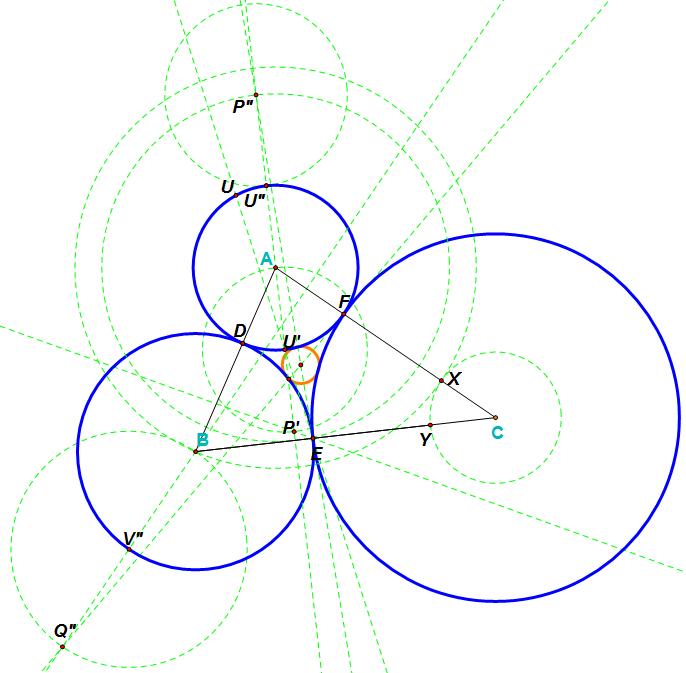
As explained above, side AB needs to be the smallest side of the triangle for this construction to work.
The point S is called the Equal Detour Point. This is the center of the inner Soddy Circle.
We have now found out how to construct all of the circles that demonstrate the answer to the coin problem.
Now consider the following poem:
The Kiss Precise
by Frederick Soddy
For pairs of lips to kiss maybe
Involves no trigonometry.
'Tis not so when four circles kiss
Each one the other three.
To bring this off the four must be
As three in one or one in three.
If one in three, beyond a doubt
Each gets three kisses from without.
If three in one, then is that one
Thrice kissed internally.
Four circles to the kissing come.
The smaller are the benter.
The bend is just the inverse of
The distance from the center.
Though their intrigue left Euclid dumb
There's now no need for rule of thumb.
Since zero bend's a dead straight line
And concave bends have minus sign,
The sum of the squares of all four bends
Is half the square of their sum.
To spy out spherical affairs
An ocular surveyor
Might find the task laborious,
The sphere is much the gayer,
And now besides the pair of pairs
A fifth sphere in the kissing shares.
Yet, signs and zero as before,
For each to kiss the other four
The square of the sum of all five bends
Is thrice the sum of their squares.
Reading just the first two stanzas of the poem, students can learn so much about the theorem. The fun part is having the students start out reading the poem and translate the poem into sentences that they can understand. Then, after the students have claimed they understand what the poem says, have them try to construct the first 3 tangent circles. For those advanced students, see if they can figure out how to construct the inner and outer soddy circles.