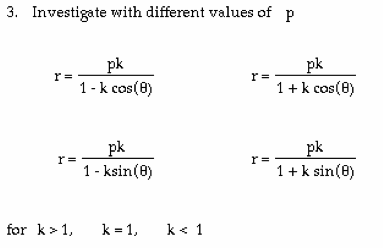
We will begin this investigation by plotting each equation above separately, for different values of p and k. Then we will look at the equations of all the graphs together.

First, we will look at the following equation,

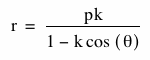
Let's see what the graph looks like for p=1 and k=1.

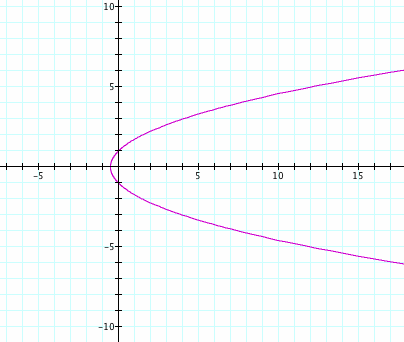
Pretty simple, we get a nice looking parabola.

Now, let's look at what happens for different values of p, while k remains equal to 1.

Below, the three graphs represent when p=1 (magenta), p = 2 (red), and p = 3 (blue).

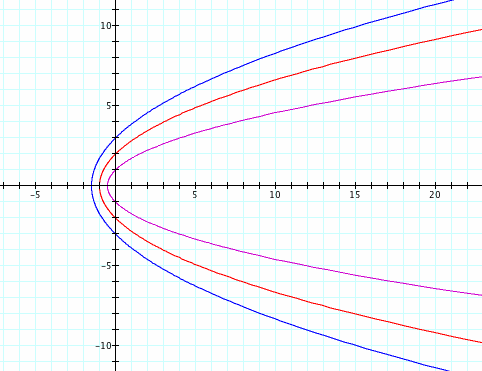
The parabola appears to get wider with a more negative vertex as the value of p increases.

What do you think will happen as the value of p decreases?

The picture below shows the function when p = 1 (magenta), p = -1 (red) and p = -2.

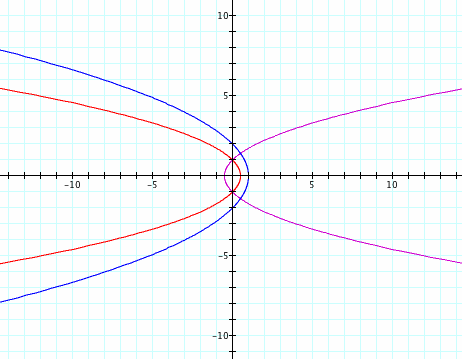
The graph is a reflection across the y-axis when p becomes negative.

What other p-values can we try? How about when p is a fraction?

Now, let's explore what happens for varying k values.

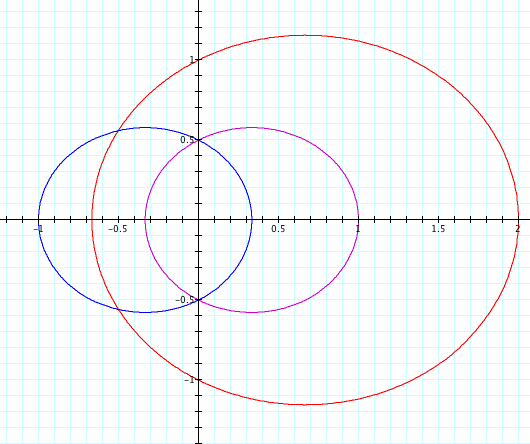
Our equation is still .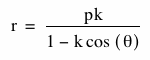

Above, we saw what happens for this equation when k = 1.

What about when k < 1?

Below is the graph for three different p - values when k = .5. The values of p are p = 1 (magenta), p = 2 (red) and p = -1 (blue).

Notice the scale of the picture above. How does this compare with the graphs when k = 1?

Now, we have gone from parabolas when k = 1 to ellipses when k = .5.

What happens with the different values of p in this case? When p increased, the ellipse became bigger (red), and when p became negative, the ellipse shifted to the left (blue).

When k is less than 1, the function will be an ellipse, no matter what p equals and when k equals 1, the function will always be a parabola.

Now, let's see what happens when k > 1.

The picture below shows the function when k = 2 and p = 1.

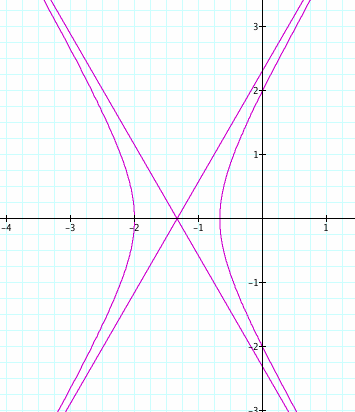
Is that what you expected? Now, we have a hyperbola, just by changing the value of k!

From our examples above, we may expect that the function will always be a hyperbola when k is greater than 1, independent of the value of p. To test this expectation, below is a graph of the function for different values of p when k = 2: p = 1 (magenta), p = 2 (red), p = -1 (blue).

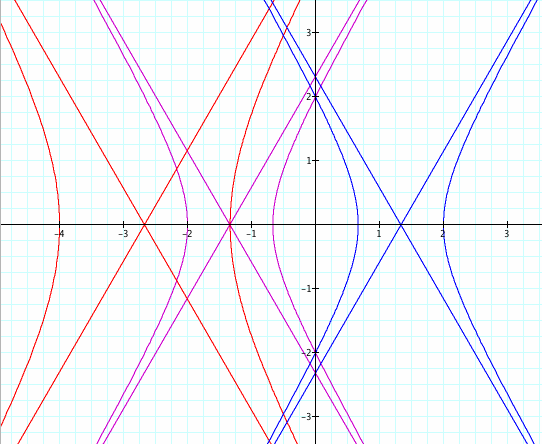
Yes, we do always get a hyperbola.

Notice the shifting that occurs here is different than the shifting we had with the parabola. When p is negative, the graph shifts to the right (blue).

Again we have the case where when p increases, the hyperbola becomes wider (red).

What have we seen with this first equation?

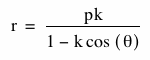
For the equation above, we can get a parabola, an ellipse, and a hyperbola, just by changing the value of k. When k = 1, the function yields a parabola. When k < 1, the function gives a graph of an ellipse. Finally, when k < 1, the function produces a hyperbola.

The values of p do shift and reflect the graph, but the shape of the graph remains the same (dependent on the value of k).

Next, we will look at the following equation,

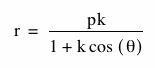
Note that the only difference between the equation above and the first equation we explored is the plus sign in the denominator where a minus sign was before. What difference do you think this will make? Will we see the same properties we did before? Will this function also give an ellipse, hyperbola, or parabola depending on the k-value?

Let's begin in the same way as before by first looking at when p = 1 and k = 1.

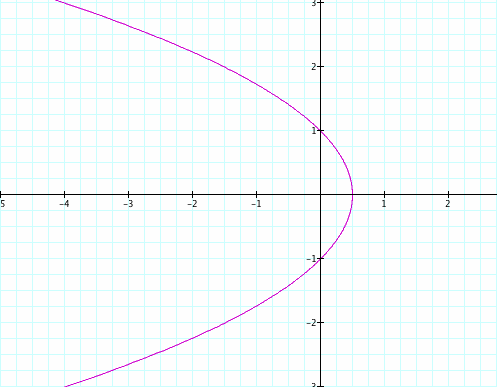
Above, we have a very similar graph to what we saw before, but now the graph is facing the left rather than the right.

Can we expect this function to be a reflection of the previous equation always?

Below, we see the first function in red and our current equation in blue for the p values 1 and -1. Again we have a reflection. (k =1 here still)

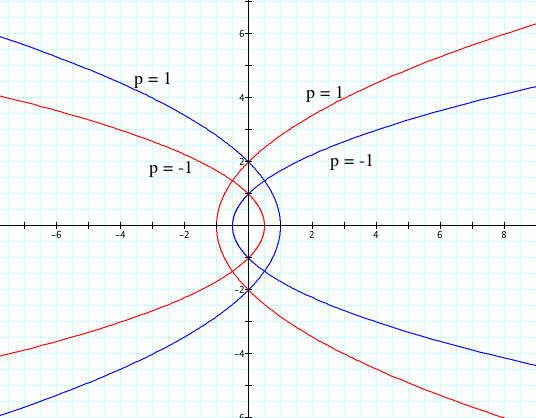
What will happen with other k-values for this equation?

The following picture is our current equation when k = .5, and p = 1 (magenta), p = 2 (red) and p = -1 (blue).

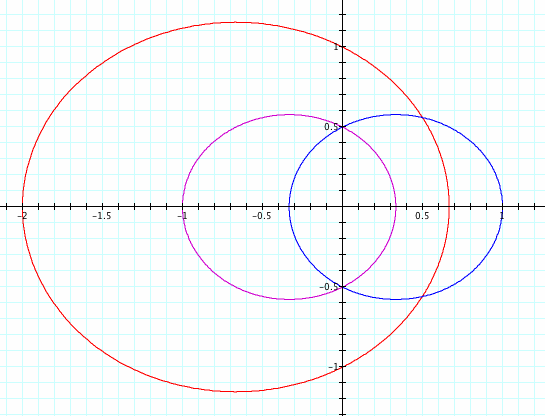
Again we have ellipses when k < 1! The pattern seems to hold.

Does the picture above look familiar? Compare it to the ellipse graph for the first equation. Again, we have a reflection across the y-axis.

What about when k >1? What do you expect?

We should expect to get another set of hyperbolas, that will most likely be a reflection across the y-axis of the hyperbolas we found in the first equation.

Below is the graph for k =2 for p = 1 (magenta), p = 2 (red) and p = -1 (blue).

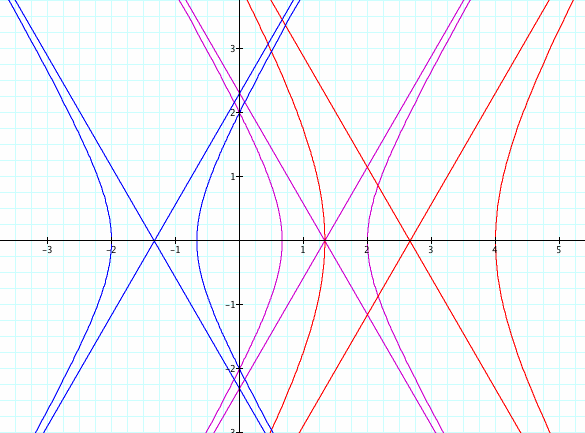
Yes! Here again, we have hyperbolas and a reflection across the y- axis. Look back at the hyperbola picture for the first equation to see this reflection more clearly.

What have we seen with this second equation?

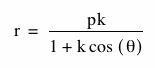
The equation follows the same pattern as the first equation: when k<1, we get ellipses, when k = 1, there are parabolas, and when k > 1, hyperbolas are produced. The graphs of this equation are all reflections across the y-axis of the previous equation.

Continuing on, we will look at the third equation,

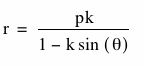
What is the difference between the current equation and our earlier equations? Here, we have the sine function in place of the cosine function. How will this affect the graphs? Will our earlier pattern of parabola, ellipse, hyperbola still hold?

Let's see what happens!

We begin once again with k = 1.

Below is the graph of the equation for when p = 1 (magenta), p = 2 (red) and p = -1 (blue).

What happened here? It looks like we still get parabolas when k = 1. Now, however, the parabolas have become vertical rather than the horizontal parabolas we had before. The pattern with the different values of p is the same, in that as p increased from 1 to 2, the parabola became wider and when p = -1, it flipped.

What about when k < 1?

A prediction can easily be made here for this case. Before, when k < 1, we got horizontal ellipses. With the parabolas, when the function changed from cosine to sine, the parabolas flipped from horizontal to vertical. See where this is going? Our prediction should be that now we will see vertical ellipses. Let's see if we are correct!

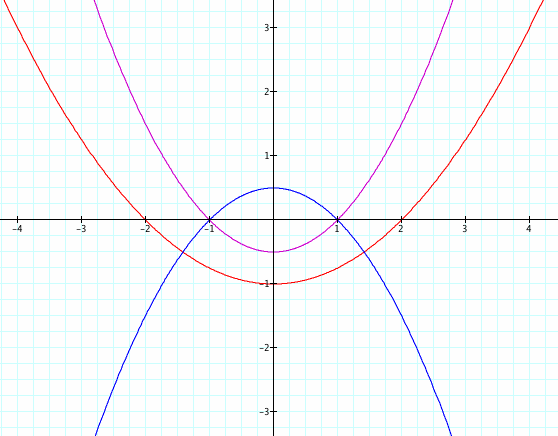
Below, k = .5 and p = 1 (magenta), p = 2 (red) and p = -1 (blue).

Yes! Again, our prediction has proven to be correct.

Can you predict what will happen when k > 1? Think about all the patterns we have seen thus far.

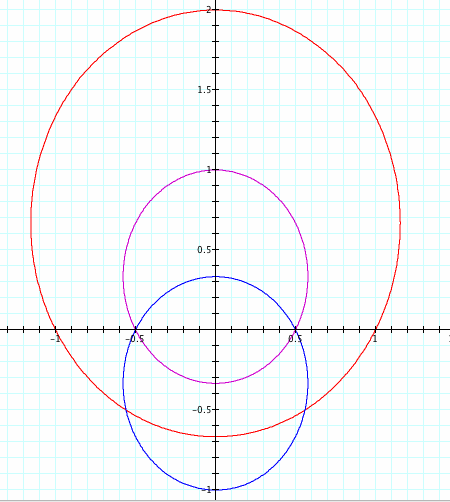
Below is the function for k = 2, when p = 1 (magenta), p = 2 (red) and p = -1 (blue).

Did you guess correctly?

Now we have vertical hyperbolas- remember, our previous hyperbolas (with the cosine function) were horizontal facing. The pattern continues!

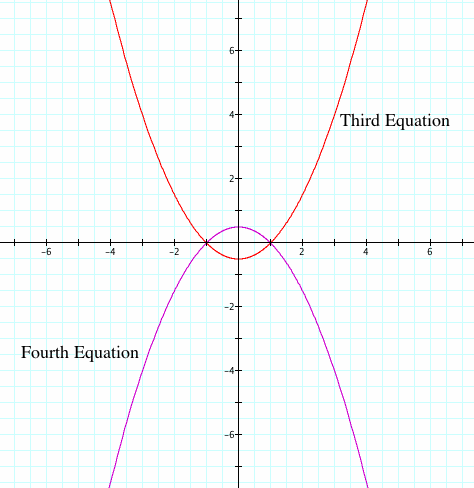
What have we seen with this third equation?

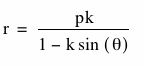
The third equation changed by replacing the cosine in the first equation with the sine function. The graph continued to hold the pattern of k = 1 being a parabola, k < 1 creating an ellipse, and k > 1 making a hyperbola. The pattern with the values of p held as well.

What changed here was the orientation of all of the conics. Before, with the cosine function, they were all horizontally oriented. Now, with the sine function, they became vertically oriented.

Lastly, we will look at the fourth and final equation,

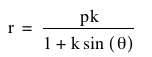
The change between this equation and the previous equation is the same subtle change between the first two equations; the sign in the denominator has changed from negative to a positive.

Since this equation change is the same as the change between the first two equations, do you think the graphical change will also be the same?

Remember that the only difference in equation one and equation two graphically was a reflection across the y- axis. May we predict a similar reflection here between the third and the fourth equations?

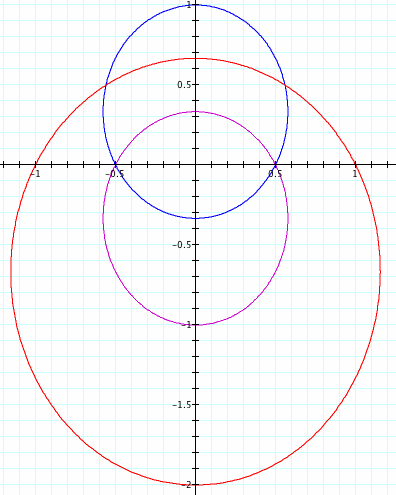
Let's look first at the case when k = 1.

Below is the graph for k = 1 and p = 1 for both the third and the fourth equations. Do we get a reflection?

We do see a reflection! This time, the reflection is across the x-axis rather than the y- axis as before with the first and second equations. This difference in axes of reflection is not strange, since we have already seen that the difference between the cosine and sine functions is a difference in the axis of orientation.

We also see that the pattern holds again, when k = 1, the graph is a parabola.

What about when k < 1?

What should we expect? From k < 1, we can predict an ellipse. Since we are in the sine function, we expect a vertically oriented ellipse. We also expect a reflection across the x-axis from the ellipses we saw in the third function.

Below is the graph for k = .5 when p = 1 (magenta), p = 2 (red) and p = -1 (blue), for the fourth equation.

Do we see everything we expected? Yes! Scroll back up to the ellipses for the third equation to see the reflection across the x-axis more clearly.

What about k > 1?

When k = 2 and p = 1 (magenta), p = 2 (red) and p = -1 (blue), what do we expect?

We expect vertically oriented hyperbolas that are reflections across the x- axis of the hyperbolas we saw in the third equation.

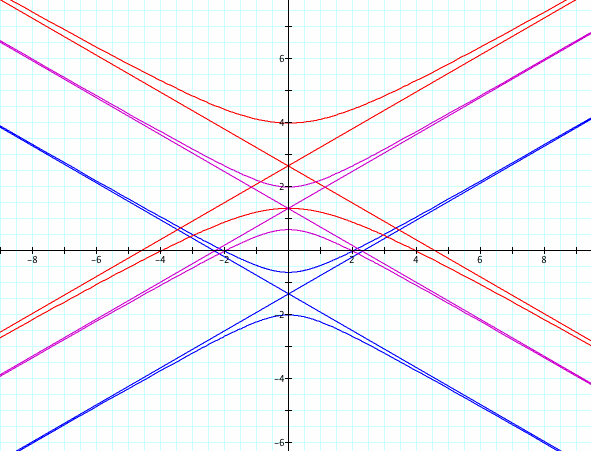
Again, we see what we expected!

What have we seen with this final equation?

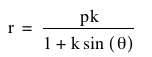
Here we have seen our patterns come full circle. The k-value pattern remains the same, as does the p-value pattern. The differences between the sine and cosine function also remained. The changes in the sign in the denominator also held, as the graph was now reflected across the x-axis.

Final Thoughts

We have seen a polar equation that follows a pattern and can quickly change its conic shape.

This investigation has taught us not only something about a particular set of polar equations, but also about making predictions about what will happen to the graphs of an equation as changes are made to that equation. We can apply knowledge of making predictions to all types of functions. Knowing how to look for changes and make predictions is an important skill. Think about other shifts, reflections, and other changes you've seen in graphs and equations.

Files saved in following format: eqn#.kvalue.pvalue(s)

Return Home