Pedal Triangles and the Simson Line

What is a pedal triangle?

A pedal triangle is a triangle in the plane that is related to a given triangle ABC. The pedal triangle is constructed from the pedal point, P, which is any point in the plane. From the point P, construct the perpendiculars to the lines created by A,B, and C. The 3 points of intersection of the perpendicular lines and the triangle lines form the vertices of the pedal triangle.

Click here for a GSP tool that constructs the pedal triangle.

Here are some examples of pedal triangles. Notice that the pedal triangle can be inside or outside the original triangle ABC, or partially inside and partially outside of triangle ABC.

The pedal triangle in the examples below is the triangle in red.

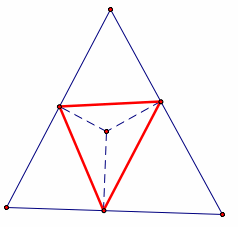
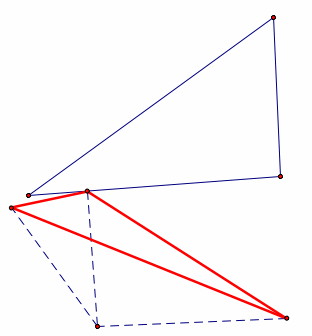
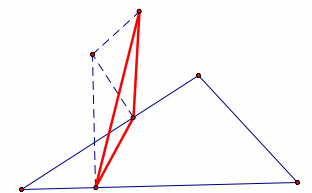
The pedal triangle can also, at certain points P in the plane, become a degenerate triangle. A degenerate triangle is a triangle where the three vertices are collinear.

Below is an example of the pedal triangle as a degenerate triangle. The pedal point has been placed on a vertex of the triangle ABC and thus created the collinear points of intersection that make up the vertices of the pedal triangle.

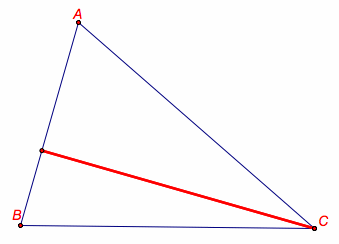
Will the pedal triangle always be degenerate when the pedal point is placed on a vertex of the triangle ABC?

Let's move the pedal point to the other two vertices of the triangle above and see what happens to the pedal triangle.

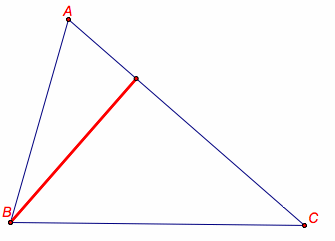
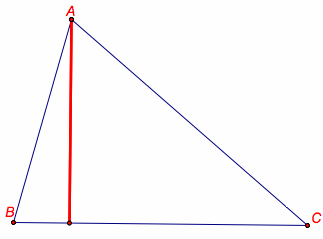
Are there other places in the plane where the pedal point will create a pedal triangle that is degenerate?

Yes! When the pedal point is located on the circumcircle of the triangle ABC, the pedal triangle is degenerate. Let's look at some examples below.

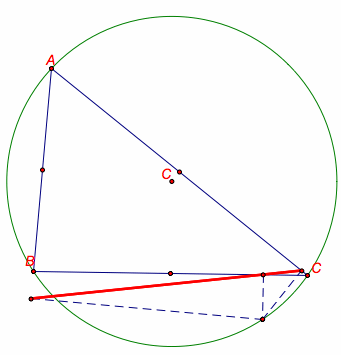
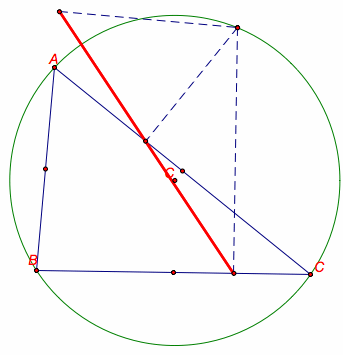
Above we see that the vertices of the pedal triangle are collinear when the pedal point is located on the circumcircle of triangle ABC.

Remember that the circumcircle inscribes the triangle ABC, so the vertices A, B, and C are points on the circumcircle. It follows that when the pedal point is a vertex, the pedal triangle becomes degenerate. Our observation earlier fits in with the new statement that pedal points on the circumcircle create degenerate pedal triangles.

The Simson Line

Above, we saw that when the pedal point is located on the circumcircle, the three vertices of the pedal triangle are collinear. The line that is created by these vertices is known as the Simson Line.

Click here for a GSP tool that will create the Simpson Line.

The Simson Line has some interesting properties.*

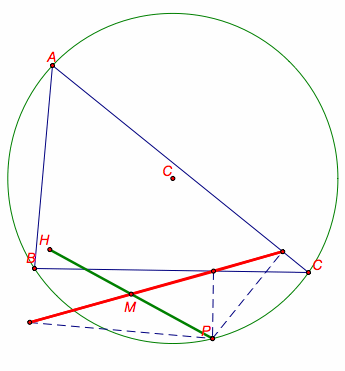
The Simson Line bisects the segment HP, between the orthocenter, H, of the triangle and the pedal point P.

In the picture below, we can see that the Simson Line intersects HP at the midpoint of HP, labeled M.

When two pedal points are placed on opposite sides of the circumcircle, the two Simson Lines of these pedal points are perpendicular.

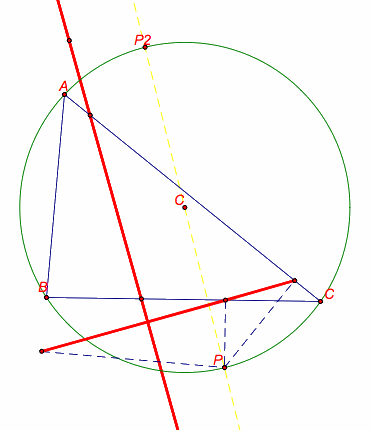
What do we see when the we trace the Simson Line as a pedal point moves around the circumcircle?

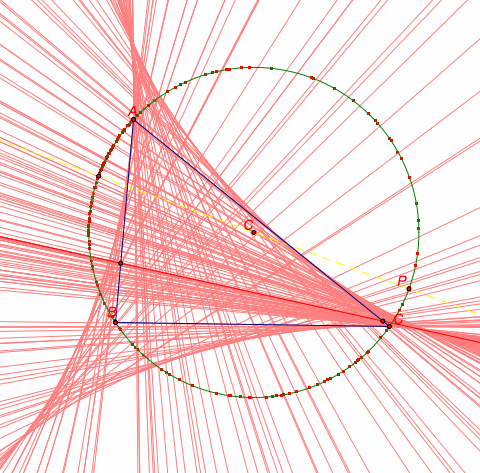
We see above that the figure resulting from the traces of the Simson Line is a deltoid.

* http://mathworld.wolfram.com/SimsonLine.html

Return Home