A Brief Introduction to Parametric Equations

Parametric Equations are not scary. They are simply a different way to represent graphs on the plane. Unlike a normal equation, the variables x and y are not functions of each other. Instead, in parametric equations, x and y are functions of a value t. It may help to think of the variable t as time. As t increases, we wonder what x and y will do.

Consider the following,

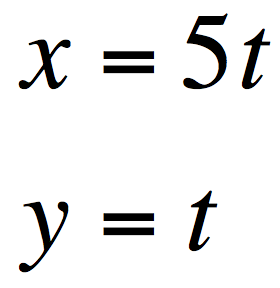
When t=0, what will happen? We get the point (0,0). When t=1, we get the point (5,1); t=2 yield (10, 2). If we were to consider values of t in between these whole numbers, we would be able to connect the points. For example, t=1/2 will give, (2.5, .5). Considering all values of t will give a more complete graph. We can also graph x and y for negative t values.

Let’s look at the graph for the above equations from the range, -2 < t < 2.

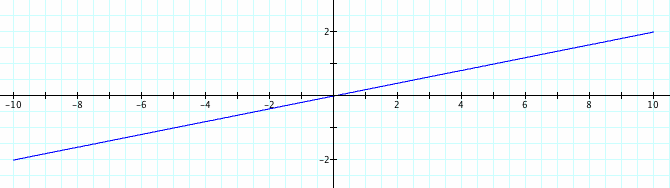
Above we see the points that we identified before on the graph.

Now, let's move on to explore a certain type of parametric equation, the Lissajous Curves.

11.

We want to look at the following parametric equations for different values of a and b.

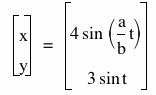
This set of parametric curves is known as the Lissajous curves.

To graph the above set of equations, we need to choose values for a and b, and also set our range of t values. For this problem, we will be looking at what happens to x and y as t goes from 0 to 50.

We want to see what the graph will look like for various values of a/b in the x-coordinate part of the parametric equation.

1. Let's begin with something simple: a/b = 1:

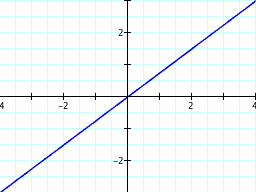
When a/b = 1, we get a straight line through the origin.

Do you think we'll always get a straight line no matter what a/b equals? What about whenever a/b equals a whole number? Let's explore!

2. We can try when a/b = 2. Do we get a straight line again?

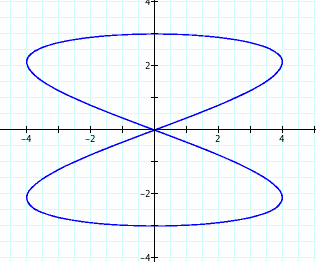
The above graph is definitely not a straight line! Changing the value of a/b really does affect what the graph looks like.

3. What do you think will happen when we double the value of a/b to 4? Will we see more loops? Or will the graph drastically change again? What do you think?

When a/b = 4, we see the following:

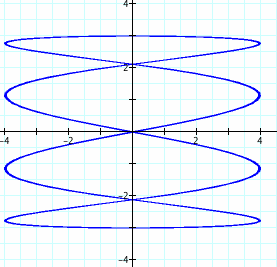
We do get double the loops! Before, when a/b = 2, we had 2 loops, now that a/b = 4, we have 4 loops.

Notice that the domain and range of the graph is the same for both a/b = 2 and a/b =4. Why do you think that is? How do you think we could change the domain and range? Hint: Look at the values for the domain and range and compare these values to the parametric equations we are graphing.

4. Have any idea what will happen when a/b = 3? A good guess may be that we would see three loops. Is that what happens?

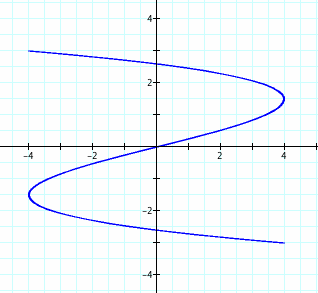
That's not three loops! Any idea what happened here?

5. The pattern we thought we had before, that a/b = number of loops, seems to have fallen apart with a/b =3. Let's see what happens with a/b = 5 to see if we can see a new, accurate pattern.

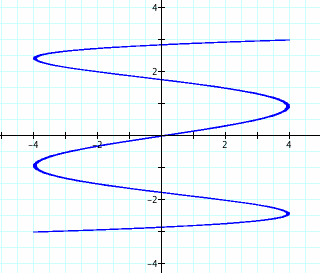
Is this similar to when a/b =3? How did it change?

6. Do you think you could make a conjecture about what's happening here? Think about the differences between when a/b is equal to an even number and when it equals an odd number?

Thus far, we have only seen what happens to the graph as a/b changes to different whole numbers. You are probably wondering what will happen when a/b is a fraction (yes, you are; well, now you are). Let's try different fractions and see what happens!

7. Let's see what happens with the fraction 1/2 = a/b. Do you think it will look anything like the graphs above?

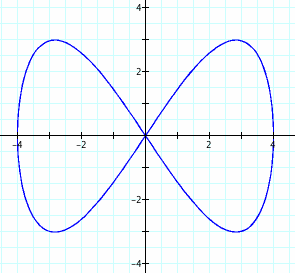
Look familiar? Compare this graph with the graph when a/b =2. It appears that this graph is the earlier graph rotated.

What about the domain and range of the graph now? Is it the same as before? Similiar?

8. Let's try another fraction. Above, we saw that when a/b = 1/2, we had the graph of a/b = 2 rotated. If a/b = 1/4, we may guess that the graph will be the graph for a/b = 4 rotated. Are we correct?

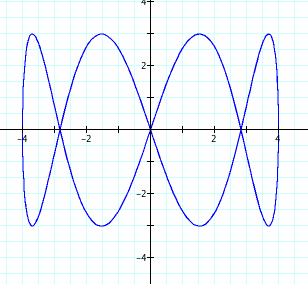
Yes! We were correct!

9. Will the rotated graph still apply for the odd numbers? Below is a/b = 1/3.

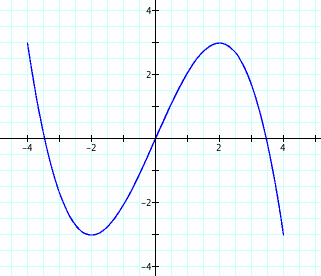
10. For a/b = 1/5?

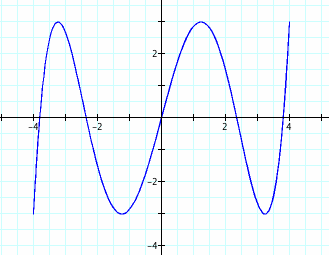
From all of the above, we see that when a/b is a fraction, the graph is a rotation of the reciprocal of the fraction. Is this always true? Let's continue and see.

11. Above, all of the fractions were reciprocals of whole numbers. What if the fraction is not the reciprocal of a whole number? Let's begin with a/b = 2/3.

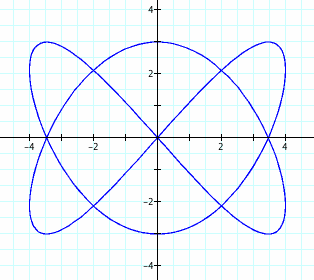
That's different! And interesting! Let's look at other fractions.

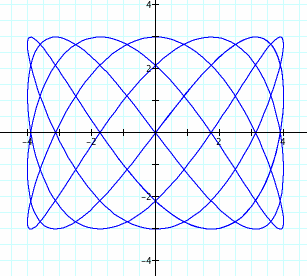
12. What happens when a/b = 4/7?

13. What about a/b = 3/5?

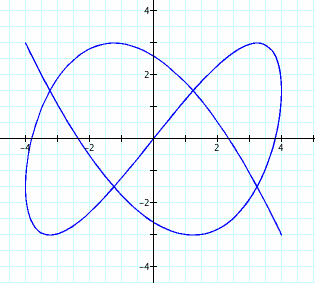
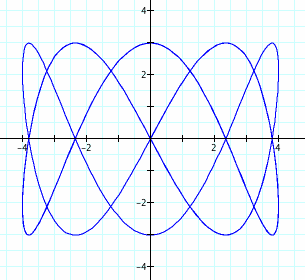
14. Let's compare a/b = 3/5 to a/b = 2/5:

15. Any ideas what will happen for a/b = 7/9?

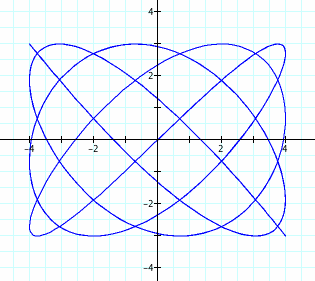
Do you notice any patterns?

Consider what happens to the number of loops as a and b increase.

Think about the differences between when a & b are both odd number and when one is odd and the other is even. (Why did I leave out the option of both a & b being even?)

Also, consider again the domain of the graphs above. What do you notice?

Further Exploration

How could you continue on with the exploration of these parametric equations? What values of a/b have we not tried here?

Consider putting in negative values for a/b. Also, what will happen when a > b, making a/b an improper fraction. Explore these graphs, look for patterns, watch the domain, and enjoy!

Comparing Parametric Equations

Let's look at comparing the Lissajous curves

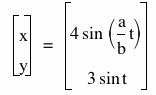
with the following parametric equation.

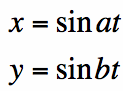
The below graphs will show the Lissajous curves in blue and the above equations in red. The values of a & b will be the same for both sets of equations.

1. What will the two graphs look like when a/b = 2?

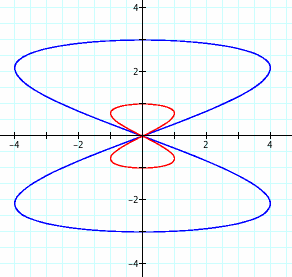
The second graph appears to be a scaled, smaller version of the original. Will this always be the case?

2. What about when a/b = 1/2?

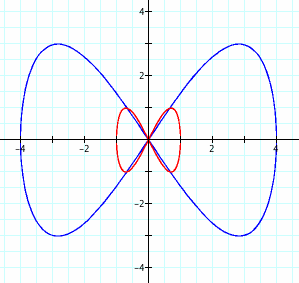
The red graph does appear again to be a smaller version of the Lissajous curve.

3. Let's try a/b = 2/3:

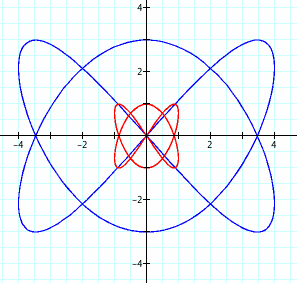
4. Finally, look at a/b = 3:

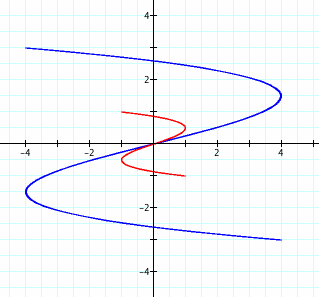
It appears that we do always have a scaled down version of the Lissajous curve for the red curve. Looking at the parametric equations, does this scaled down graph make sense?

Can you find a counterexample- a value of a/b where the red graph will not be a scaled down version of the blue curve?

Return Home