Linear Parametric Equations, 10#7 | Home

 

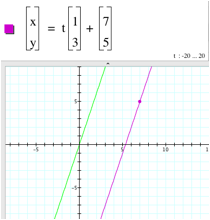
In this assignment, I explore the parameterization of a straight line through a given point.  Consider, for example, the line through the point (7,5) with a slope of 3.  Another way to think of this line is to consider the points on the line as if they were vectors. The equation for the line becomes a vector equation. To do this, we break it down and examine each of the given facts in turn.

 

First, the line in question has a slope of 3, so it is parallel to the homogeneous linear equation [x,y] = t[1,3] (*).  Every point on this line is some scalar multiple (t) of the slope vector [1,3].

 

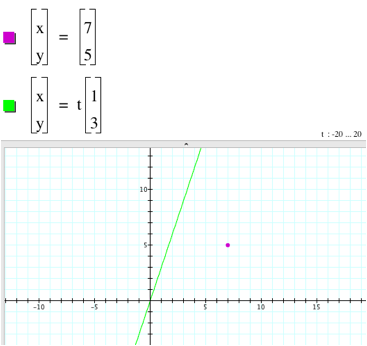
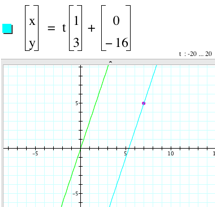
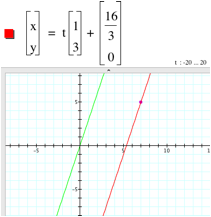
The problem with this solution, however, is that this line does not pass through the point (7,5).  The slope is correct, but how can we make this line go through the point (7,5)? Intuitively, one might think of two transformations: we could translate the line down by 3(7)-5=16 units or we could translate the line to the right by 16/3 units.  Since -16 is the y-intercept of the line, either of these will work.

 

           

 

However, it is simpler to just take the origin to the point (7,5) by adding [7,5] to our equation (*).  Although this may seem more complicated (since we are translating in two directions instead of just one), in fact, it is computationally much simpler; we don't have to compute the x or y intercept.