Polar-Form Conics | Home

 

In this exploration, I investigate the formulas for conics graphed on polar coordinates.To do this, I plot four functions and vary the values of both parameters, p and k. The parameter k is called the "eccentricity" of these conics. The four conics I investigate are given by the following formulas.

 

 

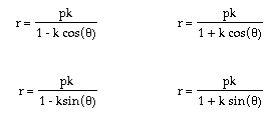
For notes on a derivation of these formulas, click here.

 

In the following movies, the four formulas above (reading from left to right, top to bottom) are labeled with the colors red, green, cyan, and blue.

 

Whenever k is less than one, the curves formed are ellipses. Observe the following movie that shows how the four curves vary with p between -2 and 2 and k set to 0.9:

 

 

Whenever k is less equal to one, the curves formed are parabolas. Observe the following movie that shows how the four curves vary with p between -2 and 2 and k set to 1.0:

 

 

Whenever k is greater than one, the curves formed are hyperbolas. Observe the following movie that shows how the four curves vary with p between -2 and 2 and k set to 1.1:

 

 

Graphing can also give a sense of what the parameter p does in each of these functions.  In the following four movies, p is fixed at -1 (notice how certain curves are reflected in the x-axis or y-axis), p is fixed at 0.1, 1.0, and 10.  Make sure you pay attention to the scale on the graphs!  It changes from movie to movie to show highlight the interesting behavior.

 

 

 

 

 

 

 

 

In summary, these movies give a picture of the role played by the parameters k and p in the formulas for conics graphed in polar coordinates.