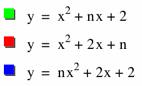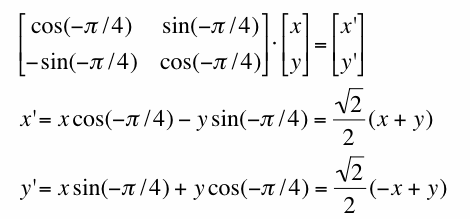Erik D. Jacobson

	Rotating Conics | Home
	The families of the graphs of quadratic equations produced by varying each coefficient are quite different. In the animation below, you can see the three graphs as they vary with respect to the three different coefficients. In particular, notice that the first coefficient (blue) varies the direction and width of the parabola for a given y-value, the second coefficient moves the vertex of the parabola along a path that appears to be a parabola, and the third coefficient translates the graph of the parabola vertically.
	Example 1.
	A variation we consider next is the equation that is quadratic in two variables. Below is an animation of for different values of n.
	Example 2.
	Another way of visualizing is by taking these curves as cross-sections of a surface in three dimensions satisfying . As you can see from the animation below, as n varies, the surface appears to smoothly change from a paraboloid to a saddle-shaped surface. The intersections of the plane z = 9 and this surface resulted in the circles and hyperbola we saw before.
	Example 3.
	It is easy to see that something unusual is happening when z = 0. Indeed, animating we see that the graph is two lines intersecting at the origin or is not defined except at zero.
	Example 4.
	If z =! 0, it appears that when n = 2, the graph is two straight lines. This is easily verified by algebra. Suppose Then and so x+y = +-2, the equations for two lines. To understand what is happening with this graph, it is helpful to change coordinates. Noticing that the conics we obtain by varying n appear to be rotated 45 degrees off the horizontal axis, we change coordinates by rotating each point 45 degrees (or pi/4 radians). Let (x, y) be a point in the graph, then its image under clockwise rotation of pi/4 can be computed by And substituting into the equation gives which is the equation for ellipses when -2 < n < 2 and hyperbola when n>2 or n <-2. We conclude that the graphs of families of equations of the form , for some constant c, are the rotations of ellipses and hyperbola by pi/4 degrees. The animation below illustrates this relationship; the original equation is graphed in red and the rotation is graphed in blue. The purple circle is the only graph that is consistent between both equations and occurs when n = 0.
	Example 5.