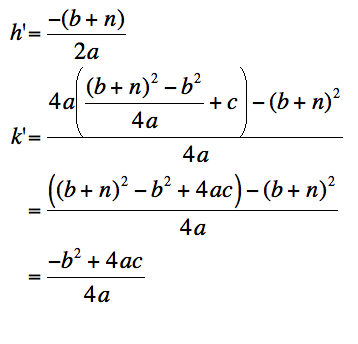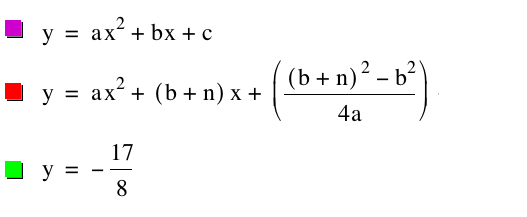Erik D. Jacobson

	Translating Quadratics | Home
	Parabolas are often given by the general form , where a, b, and c are real-valued parameters. How can one induce a horizontal translation of a given parabola's graph by changing these three coefficients? Changing the value of a changes the shape of the parabola, so this cannot work. Changing the value of c shifts the parabola up and down. Thus, it makes sense that a change of b will be required. However, more than this is needed. Changes of b, when a and c are fixed result in a parabola whose vertex appears to move along a parabola.
	Example 0.
	For a general equation , and fixed a, whenever , the graph of the parabola will have a vertex on the x-axis (hence the corresponding equation will have a double, real root). In effect, this relationship corresponds to a horizontal translation of the parabola (*). In the animation below, b varies from -10 to 10, illustrating this fact.
	Example 1.
	The reason this works is that the vertex of a parabola is . For (*), the analagous formula is , since c = 0. Increasing the value of b by n induces a vertical shift of , which can be corrected by a vertical shift of . More generally, we want to adjust the values of b and c of a parabola at vertex , to obtain a parabola with a vertex at . Letting b' = b+n, and we find that:
	The animation below, for -10 < n < 10, illustrates this relationship.
	Example 2.