Tangent Lines | Home

 

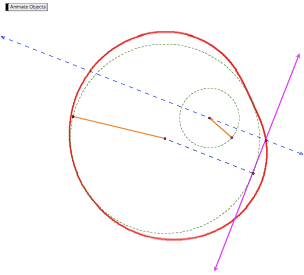
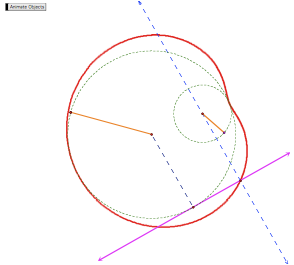
In this exploration, I use the animate feature to explore lines tangent to two circles.  In the GSP sketch below, the purple line is tangent to the left circle and the intersection of this line with a perpendicular drawn to the center of the right circle is traced in red.  Whenever the red locus intersects the right circle, then, the purple line is tangent to both circles.  In the first case, one can see that there are four possible lines of tangency.

 

 

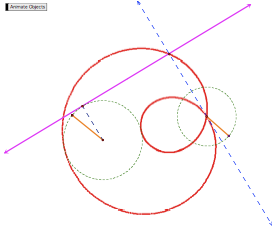
The second case occurs when the two circles intersect at a single point.  Here there are three intersections of the red locus with the circle on the right and hence, three possible lines of tangency.

 

 

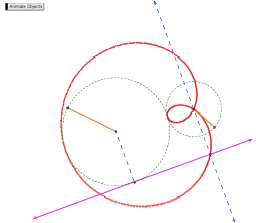
If the circles intersect twice, then there are two lines of tangency.  Note that the loop of the red locus has come entirely inside the right hand circle.

 

 

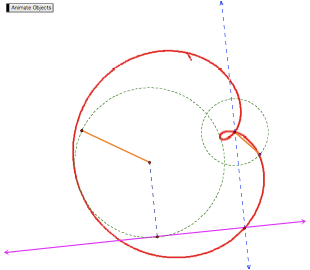
If one circle is contained within the other and there is only one point of intersection, they there is one line that is tangent to both circles, namely the line through the point of intersection.

 

 

Finally, if one circle is contained entirely within the other, then there can be no lines of tangency.  The red locus does not intersect the interior circle at all.