Final | Home

 

The problem posed concerns the grazing area of a goat staked between a silo and a shed on a 76.7 foot rope.  How much area can the goat graze on and how does this area change as the stake is moved along the line between the shed and the silo?  Further details provide are the dimensions of the shed (20 ft by 20 ft), the dimensions of the silo (radius of 20 ft), and the distance between these two (112 ft).

 

 

            (a)                                                                   (b)

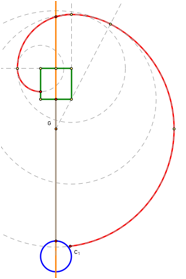
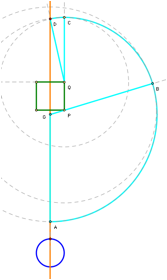
Figure 1: The area of the region bounded by the incremental spiral around the shed (a) can be found by decomposing it into circle sectors (b).

 

I began by exploring the region drawn out by the goat staked at point G. Letting the picture be oriented so that north is up, it makes sense to examine the furthest the goat can be from the stake, given a particular angle. Letting the picture be oriented so that north is up, the larger part of the goat�s range is unaffected by the silo and the shed. For these portions, the area can be described precisely as the sector of a circle.  However, when the goat�s tether encounters the southeast corner of the shed, there is a new center to the circle being traced out (namely the southeast corner of the shed) and this circle has a new radius (namely 76.7 – the distance between G and the SE corner). As the goat proceeds to walk around the building, the NE, NW, and (when G is close enough to the shed to start with) SW corners become circle centers and at each successive corner, 20 ft is subtracted from the previous radius and the area can be found by an appropriate circle sector (Figure 1).

 

 

 

                        (a)                                                       (b)                                                       (c)

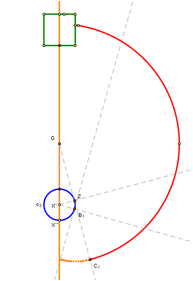
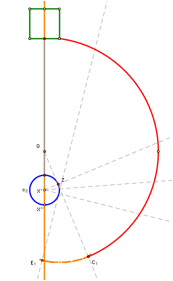
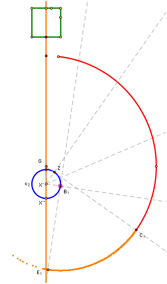
Figure 2: As the point G approaches the silo (centered at X�), the point beginning the spiral that is caused by the goat�s tether wrapping around the silo moves northward (a, b, and c).

 

When the goat moves far enough south, the silo comes into play.  The reduced reach of the goat as a result of its tether wrapping around the silo is similar to the situation with the shed.  However, in the case of the silo, the changing center of the circle and the radius of this circle are continuous functions instead of step functions.  In particular, one can calculate the length of the tether from the last point it touches the silo (point B in Figure 2) to the goat by subtracting from 76.7 the arc length between B and the original point of tangency Z and the distance from G to Z.  Integrating this function will give the area of this region.

 

Note also, that an accurate complete solution would subtract all or part of the shed area (400 ft²) and the silo area (100� f t²), depending on where the goat is staked.