

Compound Interest: A Double-edged Sword
by
Rui Kang
Compound Interest: A Double-Edged Sword
In this investigation, we look at the magic of compound interest from both a lender and a borrower perspective.
The great Albert Einstein once called compound interest "the greatest mathematical discovery of all time" and "the eighth wonder of the world".
Let's explore this powerful concept together using examples such as bank savings and credit card debt.
The teaching of compound interest cannot be overvalued especially at a time of worldwide economic recession.
A 2001 Harris Interactive survey found that nearly half of the college seniors surveyed felt "not very knowledgeable" or "not very knowledgeable at all"
regarding financial decision making. While most college students rated home ownership, life insurance, 401(K), and IRAs as important financial instruments,
few demonstrated high levels of knowledge about them. The surveyed college students, on average, held three credit cards; most of them already had incurred significant debt.
A 2005 Harris Interactive survey found that the trend of low economic literacy among America's teens and adults is continuing.
The average grade for the adult respondents for a 24-question quiz on basic economic and personal finance concepts was 70(C);
for high school students the average was 53(F). About 60% of the high school students and a little more than 25% of the adult respondents failed the quiz.
Only one-third of the adults and less then 10% of the high school students managed to answer at least 80% of the questions correctly.
In addition, both adults and students showed a poor understanding of concepts
related to personal finance such as income, money management, savings and investment, spending, and credit.
So let's begin our exploration of compound interest without further delay.
Lender's Perspective:
First, let's discuss compound interest from a lender's perspective. If you deposit your money in a savings account at a bank, then you lend your money to the bank.
Under this scenario, compound interest will work magic for you probably more than you can ever imagine.
Then what is compound interest? How is it different than simple interest?
A simple answer to these questions is:
Simple interest pays you interest on your principal;
but compound interest pays you interest on your principal and as well as the previous interest that you have earned. Let's look at a basic example:
You have two friends, Mary and Jane. Mary has a $10, 000 investment that pays 10% simple interest annually.
Jane, on the other hand, only has $5,000 to invest, but in an account that pays 10% compound interest annually instead of simple interest.
Both Jane and Mary plan to invest their money for a period of 30 years. So after 30 years, how much money will each of them have?
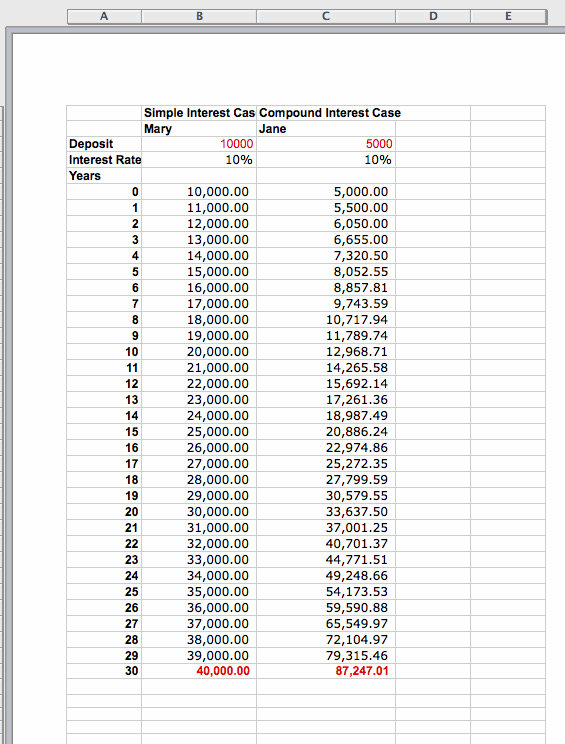
We have noted that Mary starts with twice as much money as Jane has, but ends up having less than half of what Jane has after 30 years.
This simple example leads us to other questions:
(1) How about we deposit $100 dollars per month for 30 years rather than make only a one-time sum of investment? Then what will happen?
(2) How do banks calculate compound interest? Is it annually compounded, quarterly compounded, or monthly compounded?
Will that make any difference?
Before we move on to the next example, let's observe the following formula:
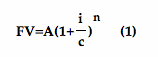
In this formula,
FV: future value,
A: one-time investment (not annuities),
i: interest rate
c: # of compound period per year
n: # of compound periods
Exercise: Use formula (1) to calculate the amount of money Jane will have after 30 years if she invests in a savings account that pays 10% interest, compounded annually.
Compare your result with that obtained from the spreadsheet earlier, and they should match each other roughly.
(Note in Jane's case, A is 5,000, i is 10%, c is 1, and n is 30. Do you know why?)
Now let's modify this formula a little bit to take into account that a person may invest monthly instead of putting a one-time sum of investment.
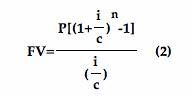
Comparing (1) and (2), we find that only one variable appears to be different between the two formulas, i.e., P versus A.
We know from (1) that A means one-time investment, but P here means periodic investment.
Now we are ready to examine a more realistic example,
Suppose Jane, instead of putting a $5,000 one-time investment for 30 years, desides to deposit $100 per month into her savings account,
which pays her 8% annual interest rate. Then after 30 years, how much money will Jane have?
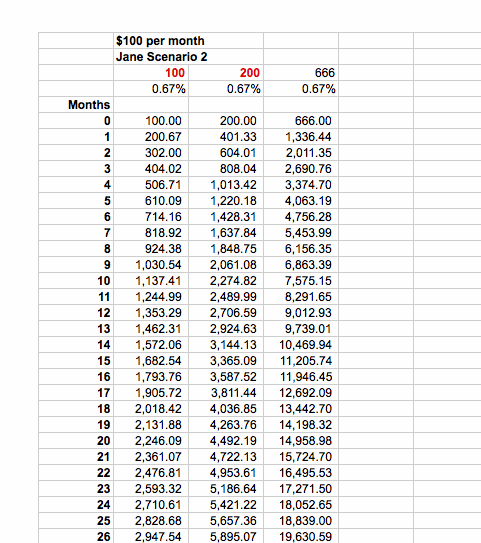
.gif)
Yes, you have noticed that $100 per month has turned into a whopping $150,130 in 30 years.
If Jane decides that she wants to deposit $200 per month into her savings account, everything else held constant,
then how much money will she have in 30 years then?
Using the same Excel sheet, we find that she will have about $300,259!
Exercise: Use formula (2) to calculate the amount of money Jane will have after 30 years
if she invests $100 or $200 in a savings account that pays 8% annual interest, compounded monthly.
Compare your result with that obtained from the spreadsheet earlier, and the results should match each other roughly.
(Note that in this second scenario, P is $100 or $200, i is 8%, c is 0.67%
(annual interest rate is 8%, but compounding occurs every month, so we turn this annual rate into monthly rate for our calculation, i.e., 8%/12=0.67%),
n is 12*30=360
(since compounding occurs every month, we have a total of 12 months * 30 years=360 compounding periods))
Now we may ask the question which one is more to my advantage: yearly compounding? quarterly compounding? monthly compounding? or daily compounding?
Let's use the following example to help us answer this question:
Suppose today you have $10,000 to invest in a savings account that pays an annual interest rate of 8%.
Does it make a difference how frequently the money is compounded?
We will look at three scenarios and under each how much money we have after 30 years:
yearly compounding (8%, 30 periods), quarterly compounding (2%, 120 periods), and finally, monthly compounding (0.67%, 360 periods)
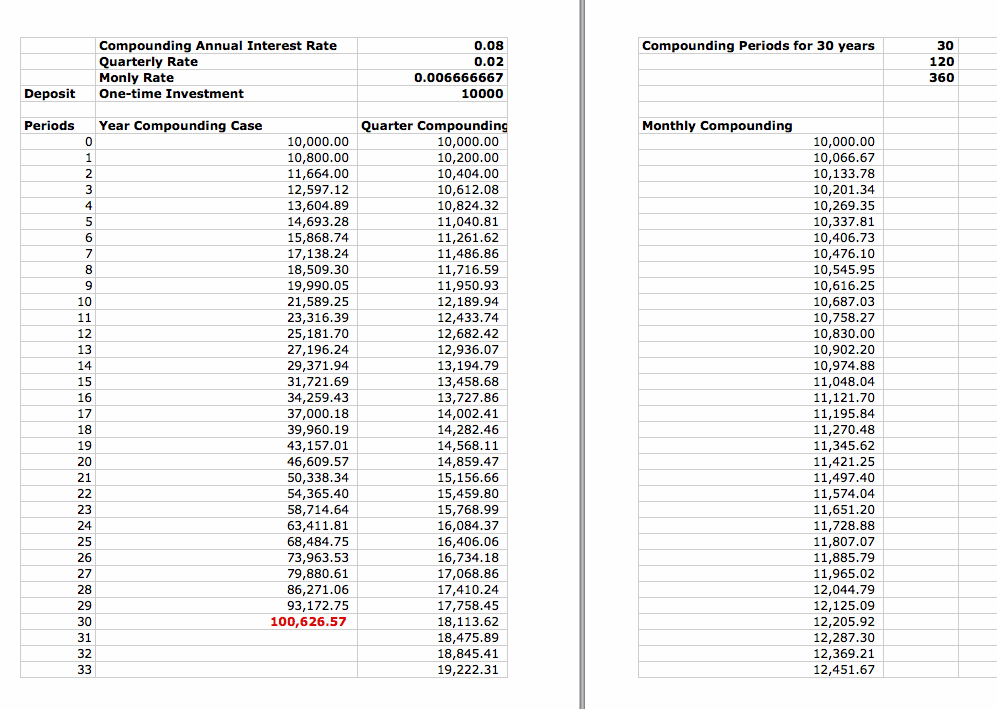
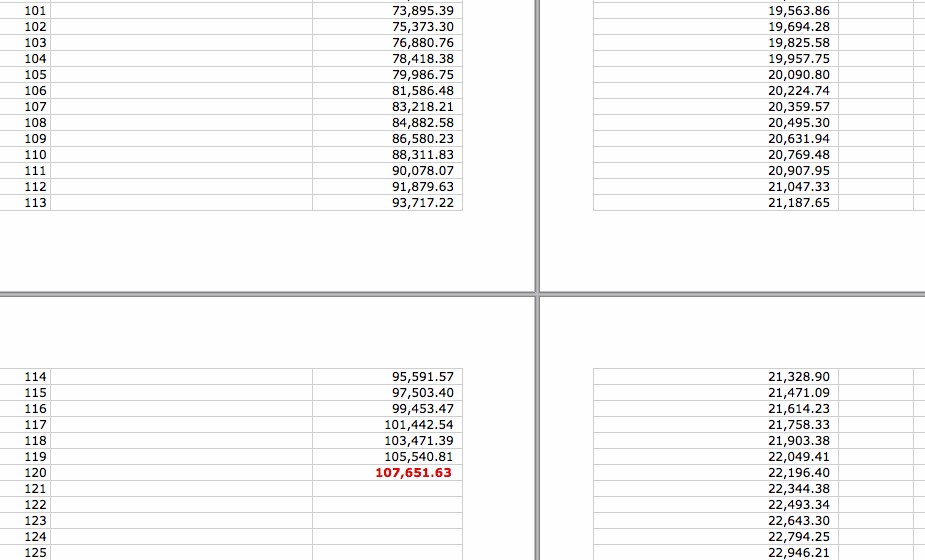

We have noticed from the spreadsheet that in fact, we will have about $100,626 if our money is compounded annually,
$107, 651 if compounded quarterly, and $109,357 if compounded monthly.
So obviously among the three, monthly compounding is more to our advantage as compared to yearly or quarterly compounding.
In fact, the more frequently our money is compounded, the more money we will get if everything else held constant.
So what conclusions do you draw about daily compounding? or even continuous compounding?
Exercise: use formula (1) to calculate what amount of money we will have after 30 years
if we invest $10,000 in a savings account that pays at annual interest rate of 8% under three cases:
yearly compounding, quarterly compounding, or monthly compounding. Your results should match roughly the earlier results obtained from the spreadsheet.
At this point, you might find it interesting to work backwards,
for example, to know how much money should we deposit in a savings account that pays 8% annual interest rate, compounded monthly,
in order to obtain 1 million dollars in 30 years?
Of course, now formula (2) comes in handy and you can plug in the corresponding numbers into a calculator or spreadsheet.
But we may also use the trial and error method to approximate this number.
Let's go back to Jane's scenario 2 in which she deposits $100 per month, for a period of 30 years, into a savings account that pays 8% annual interest, compounded monthly.
We know she will get about $150,130 in 30 years from our earlier calculation.
Now let's play with this example by changing the amount of periodic payment until we get close to 1 million dollars after 30 years:
.gif)
.gif)
By trial and error, we find that if Jane deposits approximately $666 per month into the specified account,
she will become a millionaire in 30 years! Completely doable, right?
Exercise: As before, now it is time for you to use formula (2) to verify this result.
Next, let's look at one more example which illustrates the importance of timing when it comes to taking advantage of compounding interest.
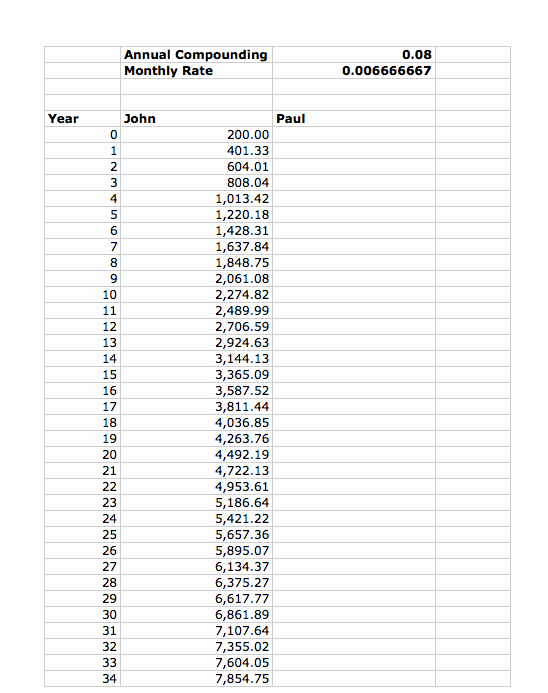
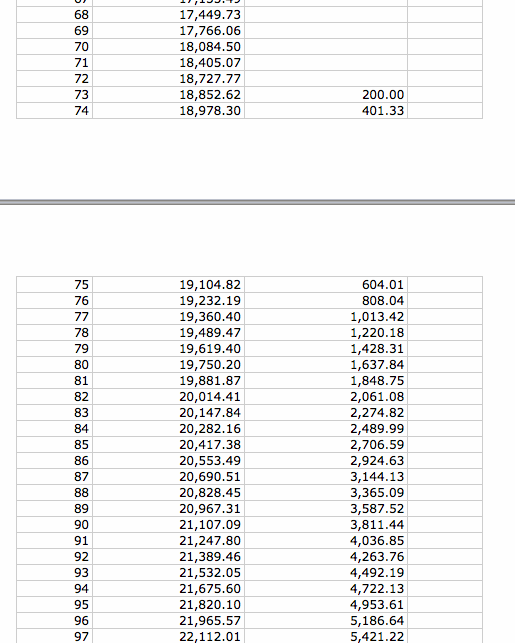
Here is an example: Suppose again, you have two friends, John and Paul.
John invested $2,400 ($200 dollars per month) for 6 years straight into a savings account earning a fixed 8% annual interest rate, compounded monthly.
After the 6th year, Bill stopped investing and let his account grow as the compound interests accumulate.
At the same time, let us assume Paul deposited zero for the first 6 years.
But after the 6th year, Paul starts to put $2,400 ($200 dollar per month) into a 8% savings account, compounded monthly,
and continues to add this same amount every year and doesn not stop.
Since Paul started 6 years later than John, how long will it take Paul to continue putting money into his account after the initial missed 6 years,
until his balance will eventually be greater than John's?
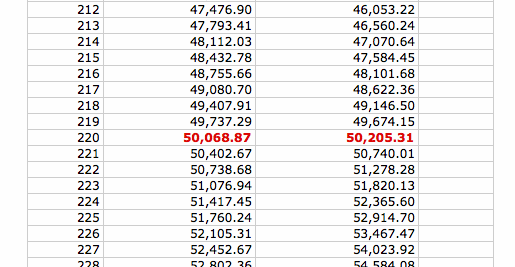
The answer is about 12 years. At that time, Paul's total account balance will be $50,205, compared to John's $50,068.
John's total out-of-pocket investment of $200 for 72 months is $14,400.
Paul on the other hand has to contribute $200 for 144 month for a total of $28,800 to ultimately beat out John's account balance.
In summary, it takes Paul twice amount of time in order to make up for the 6 years he missed,
and it takes him twice amount of money to be just as rich as John after 12 years.
Now you may play with the numbers and see other possible scenarios:
For example, John started out 10 years earlier than Paul instead of 6 years.
John and Paul invested in an account that pays 10% interest instead of 8%.
John and Paul decided to contribute $500 per month instead of $200, what happens under each of these scenarios?
Summary:
Borrower's Perspective:
Compound interest can do magic if you lend, save, or make money.
However, it can work against you if you are on the other side of the game, say, you have to borrow money to purchase something you desire.
This is because the interest charged for borrowing money on credit card debt, for home mortgage, and for car loans are also compounded.
Although you may receive tax deductibles if you borrow money to buy a house,
using credit card for everyday purchases will only make you more indebted without the same kind of tax benefit.
Yes, compound interest works pretty much like a double-edged sword!
In the United States, children as young as age three already begin to experience purchasing power and are labeled as consumers by industries.
It is not unusual to see a young college student holding 3 or 4 credit cards and having already incurred significant debt.
Somebody told me that they don't feel like they were spending as much money if a piece of plastics is swiped unless "real" money changes hand.
After all, when we spot something we have desired for a long time,
how can we curb the urge to spend even though our rational reasoning tells us that our credits have already been overextended or overstretched?
Let's consider a simple example: Every month, Jack borrows $1,000 on his credit card with a fixed 24% annual interest rate.
Suppose the credit card requires a minimum payment of 5%, and Jack thinks,
paying $50 a month is a piece of cake because he earns money from working at a campus cafeteria for $10 dollars per hour and 20 hours per week (or $800 per month).
But let's see what will happen after 6 months if Jack only pays off the minimum payment:
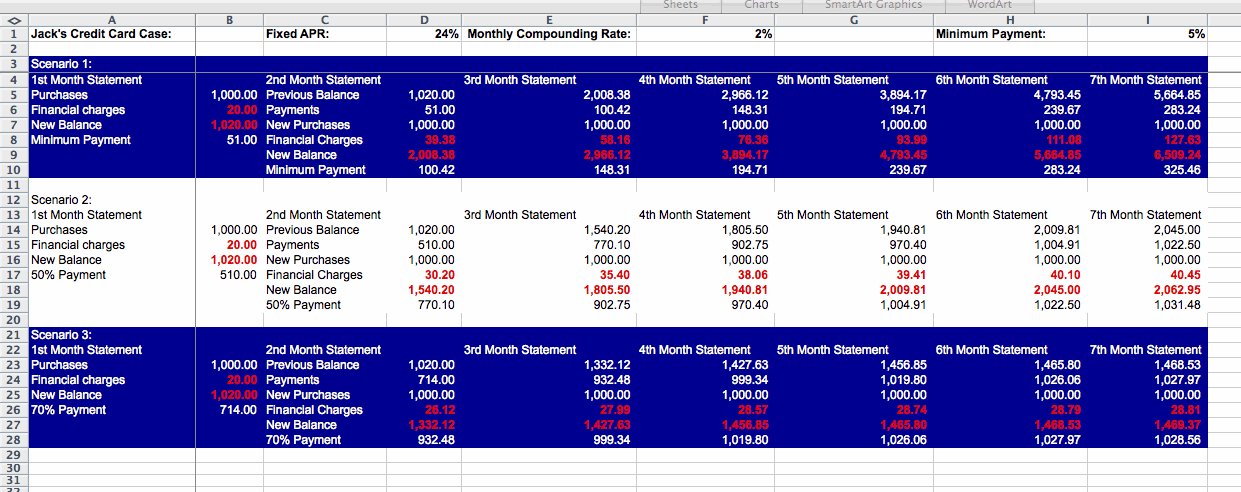
We have noticed that if Jack only pays off the minimum payment, his debt will accumulate to around $6,500 after merely 6 months,
and his financial charge grows from only $20 dollars to about $127, or 6 times as much as the initial financial charge! I
f we focus on what happens between the 1st and 2nd month, we will notice that even though Jack pays $51 off his first month's $1,020 debt,
but since his financial charge almost doubles, he only pays off around $51-$20 or $31.
But if Jack decides to pay off 50% of the money he owes and has the ability to do so, his debt will amount to only about $,2000 after 6 months,
and his financial charge will grow from $20 to about $40 dollars.
You probably would say this still does not look too good, but much better than the first scenario, right?
If Jack has the ability and discipline to pay off 70% of what he borrows each month, then his debt will only grow about $500 dollars in half a year,
and his financial charge increases from $20 to about $28, or by only 8 dollars. This sounds much better than the previous two cases.
Now you may try to play with these numbers to see what happens if Jack borrows $500 per month instead of $1,000,
what happens if the financial charge is 2.5% per month instead of 2%,
or what happens if Jack can pay off 90% of his debt per month?
Of course, the ideal case is that Jack will pay off whatever he borrows each month so that the credit card company will not be able to charge him any interest at all.
If you are still not convinced, here is another illustration of how compound interest can work against you if you have outstanding balance:
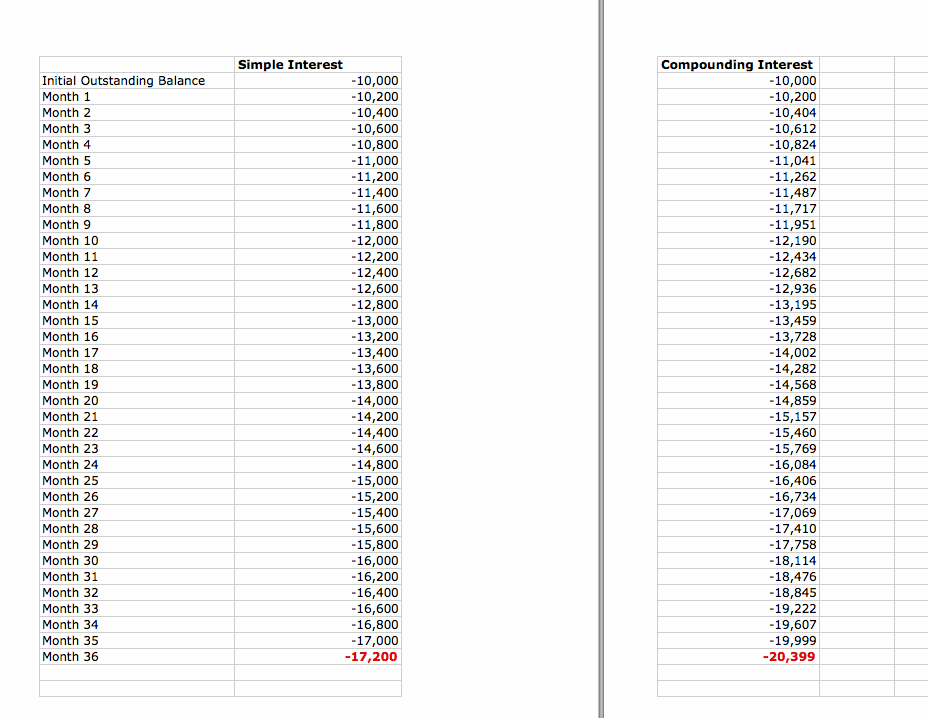
Suppose you have an outstanding balance of $1,000 with a fixed 2% monthly interest rate,
then after 3 years how much do you owe if the interest is simple versus compound?
With compound interest, you will owe about $2,000 in three years, but with simple interest, you owe about $1,700, a $30 dollar difference.
You might say, it does not make too much of a difference if you use simple or compound interest.
But imagine you owe not $1,000 but $10,000, then what will be the difference? The answer is about $3,200!
Then imagine you do not pay that outstanding balance for 5 years instead of 3 years, then what will be the difference?
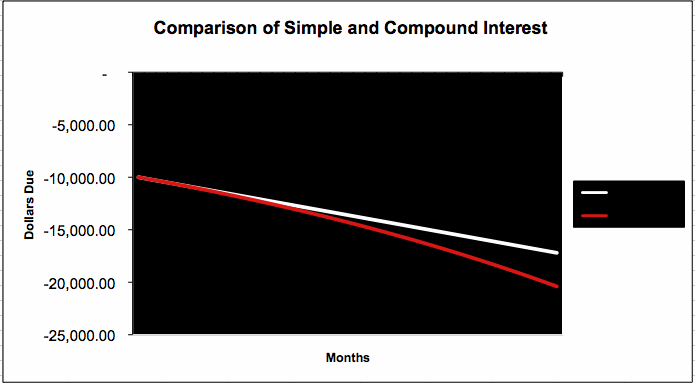
If we observe the two series in the graph below, we can easily find out that simple interest works like a linear function or a straight line (the white line),
and compound interest, on the other hand, works like an exponential function or a curved line with a steeper slope (the red curve).
Let's recall the formulas we presented earlier for calculating future value using compound interest:
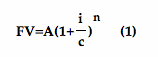
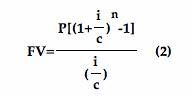
We have confirmed that both of them represent exponential functions.
Then how about simple interest? In fact the formula looks like:
FV=A+A*i*n
FV: future value,
A: amount invested or owed,
i: interest rate,
n: # of period
Clearly, this formula represents a linear function.
Therefore, mathematically, simple interest represents a linear function and compound interest represents an exponential function.
Let's go back to Jane's case presented at the beginning of this investigation:
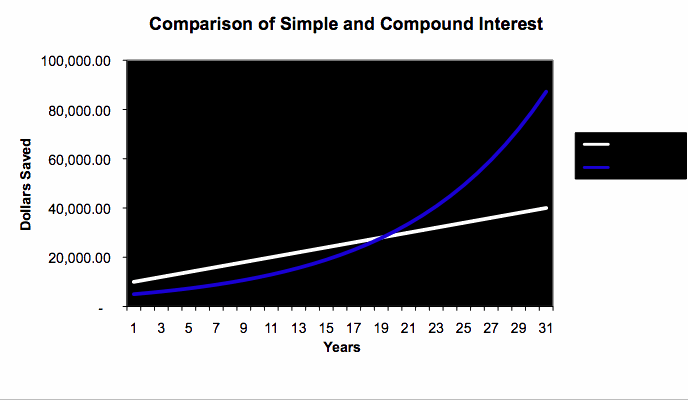
We have noticed from the graph above that again compound interest (the blue curve) works exponentially, but simple interest works like a linear function (the white line).
However unlike the case shown in the earlier graph, this time, compound interest works to our favor by helping our money grow much more rapidly than simple interest.
Summary:
A final warning: APR versus APY:
When you're borrowing money, for example, from a credit card company, you are quoted an APR (Annual Percentage Rate).
But when you're saving money, for example, at a bank, you are quoted an APY (Annual Percentage Yield).
Then you may ask what is the difference between APR and APY?
APR represents a simple rate. But your credit card company often calculates your debt using monthly compounding.
Therefore, your balance will grow faster than this rate indicates.
If your outstanding balance is large or your credit card company compounds more often, you are more in debt.
But APY is the percentage difference between your starting balance and your ending balance over a year.
If you withdraw certain amount of money before the end of a year,
you won't have earned the quoted APY by the end of that year because banks compound monthly instead of yearly.
If your account is large, the difference can be significant.
The following Excel file contains all of the above investigations.
If you are interested in replicating any of the above analysis, please plug in different numbers in this file.
If you want to create your own Excel file for investigating compound interest or other similar topics,
you may click on each cell and study the formulas used to generate each of the above analyses.
References:
http://www.moneybluebook.com/the-power-of-compound-interest/
http://www.thesimpledollar.com/2006/11/28/explaining-simple-interest-compound-interest-apr-and-apy/
http://bobhurt.com/compound_interest.htm
http://www.monetos.co.uk/financing/credit-cards/interest-rates/compound-interest/
http://www.infohq.com/CPA/SavingsandInterest.htm
Markow, D., & Bagnaschi, K. (2005). What American teens & adults know about economics. A report prepared for the National Council of Economic Education.
Retrieved May 17, 2009, from http://www.ncee.net.http://www.infohq.com/CPA/SavingsandInterest.htm
Martin, A., & Oliva, J. (2001). Teaching children about money: Applications of social learning and cognitive learning developmental theories.
Journal of Family and Consumer Sciences, 93(2), 26-29.