Assignment I: Parameters of sin Function
by
Rui Kang
Examine graphs of y=asin(bx+c) for different values of a, b, c
First, let's observe the basic sine function graph: y=sin(x).
Note in this case, a=1, b=1, and c=0
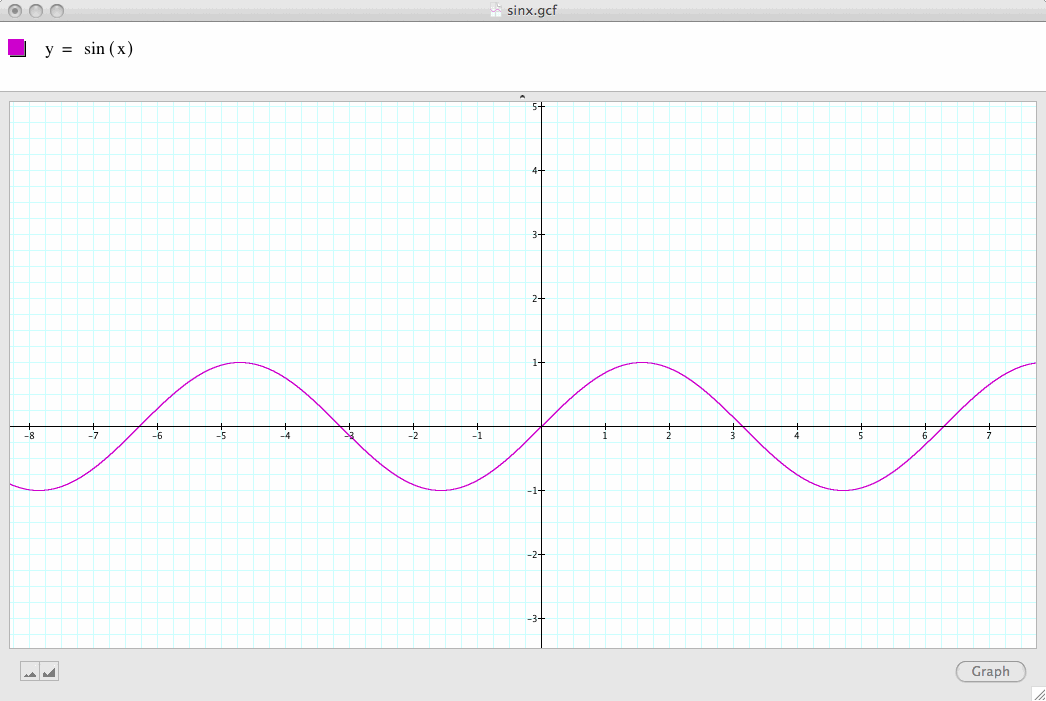
Now let's summarize some of the key properties of this basic sine graph:
The next two graphs examine what happens if we keep b and c constant and vary the value of a:
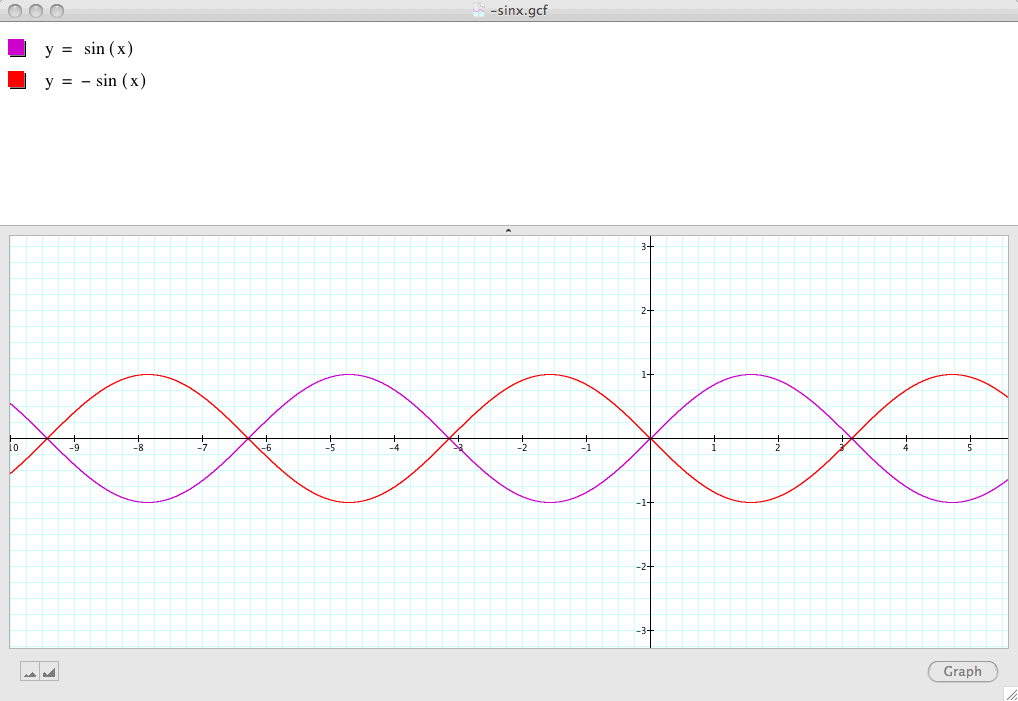
Now, let's change a=1 to a=-1 and see how that affects the graph
Note that if we reflect y=sin(x) with respect to the x-axis, we get y=-sin(x). Everything else remains the same.
Next, let's observe what happens when a=2, i.e., y=2sin(x):
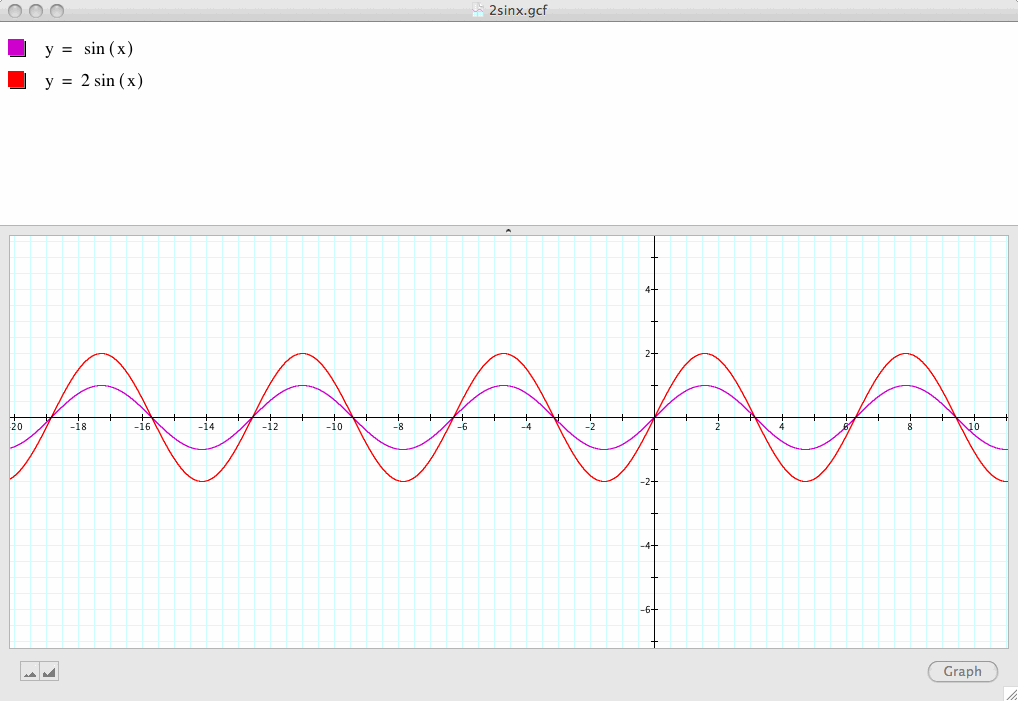
We see the domain of the sine function in this case is still the set of all real numbers; however, the range of the sine function now becomes [-2, 2].
If we keep on trying other values of a, for example, a=3, a=-4 and etc., we can generalize these different situations to the following:
Conclusion 1: We say that parameter a affects the range of the sine function, which can be written as [-|a|, |a|].
The next two graphs demonstrate what happens if we keep a and c constant and vary the value of b:
Now, let's change b=1 to b=2 while a is still 1 and c is still 0 as in our original case:
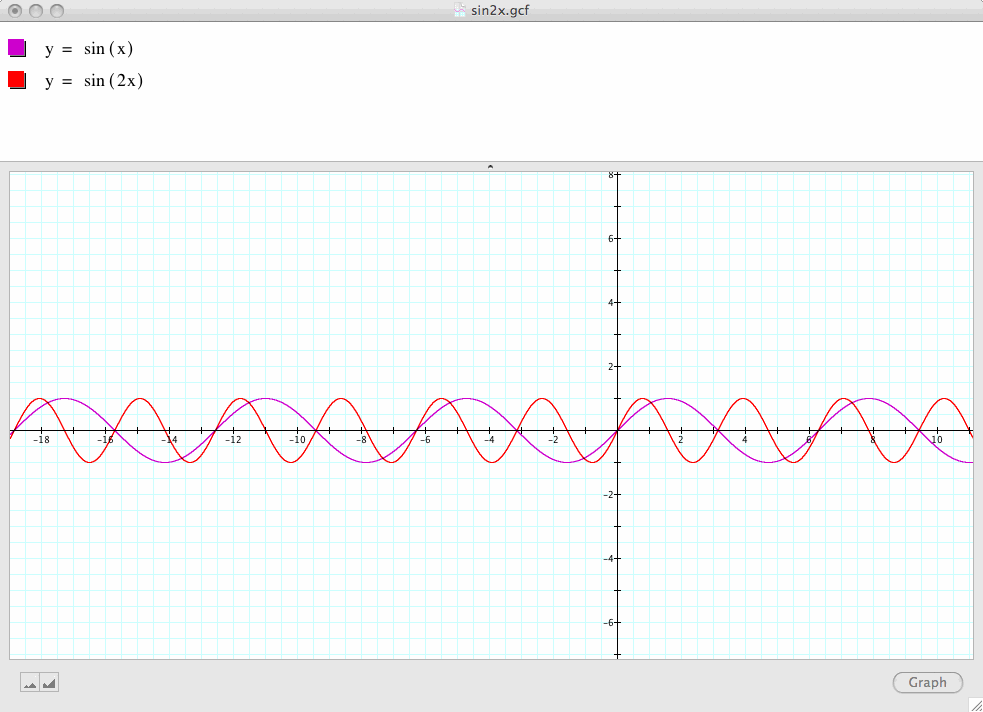
Note that the domain of sine function in this case is still the set of all real numbers; the range is like the original case y=sin(x), i.e., [-1, 1]
However, one period of this sine function now becomes ![]() instead of
instead of ![]() .
.
Next, let's change b=1 to b=1/2 while a is still 1 and c is still 0 as in our original case:
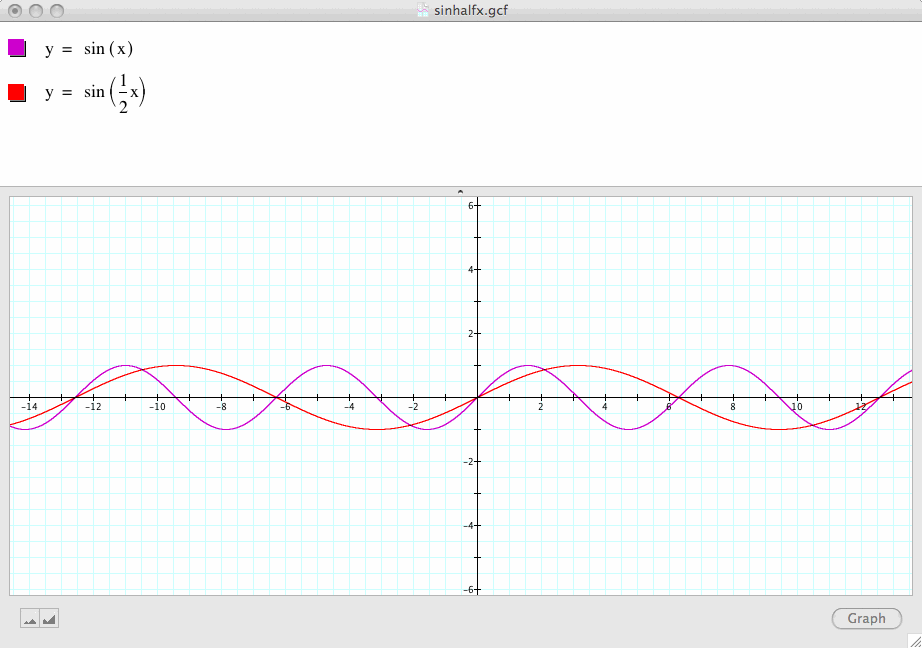
Note that the domain and range of this graph remain the same as those in our original case.
However, one period of this sine function now becomes ![]() instead of
instead of ![]() .
.
Conclusion 2: We say that parameter b affects the period of the sine function, which can be written as ![]() /(|b|).
/(|b|).
A side note is that in both of the above two examples, b>0.
But if we have y=sin(-2x) instead of y=sin(2x), we observe that the two graphs are exactly the same except that sin (-2x) is the reflection of sin(2x) with respect to the x-axis.
But according to an earlier investigation, we expect that -sin(2x) is the reflection of sin(2x) with respect to the x-axis.
If we continue to try different values, we can generalize that sin(-bx)=-bsin(x).
In the next two graphs, we investigate what happens if we keep a and b constant and vary the value of c:
Now, let's change c=0 to c=1 while a is still 1 and b is still 1 as in our original case:

Note that the domain and range of this graph remain the same as those in our original case.
In addition, one period of sin(x+1) is also the same as one period of sin(x), and both equal to ![]() .
.
However, we find that the graph of sin(x+1) as compared to sin(x) has a phase shift to the left by 1 unit.
Now, let's change c=0 to c=-1 while a is still 1 and b is still 1 as in our original case:
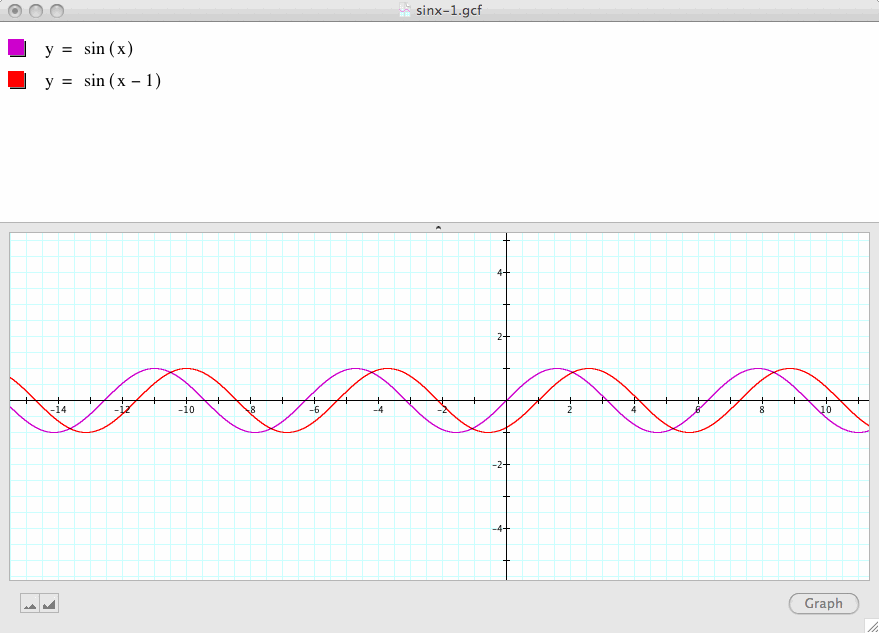
Note that the domain and range of this graph remain the same as those in our original case.
In addition, one period of sin(x-1) is also the same as one period of sin(x), and both equal to ![]() .
.
However, we find that the graph of sin(x-1) as compared to sin(x) has a phase shift to the right by 1 unit.
Now we can try more values of c such as 2, -3, 4 and etc. Eventually, we feel that we can generalize these situations to the following:
Conclusion 3: We say that parameter c affects the phase shift of the sine function.
In particular, the sine graph shifts either to the right or to the left by c/b units. If -c/b>0, the shift will be to the right; if -c/b<0, the shift will be to the left.
Finally, let's put everything together!
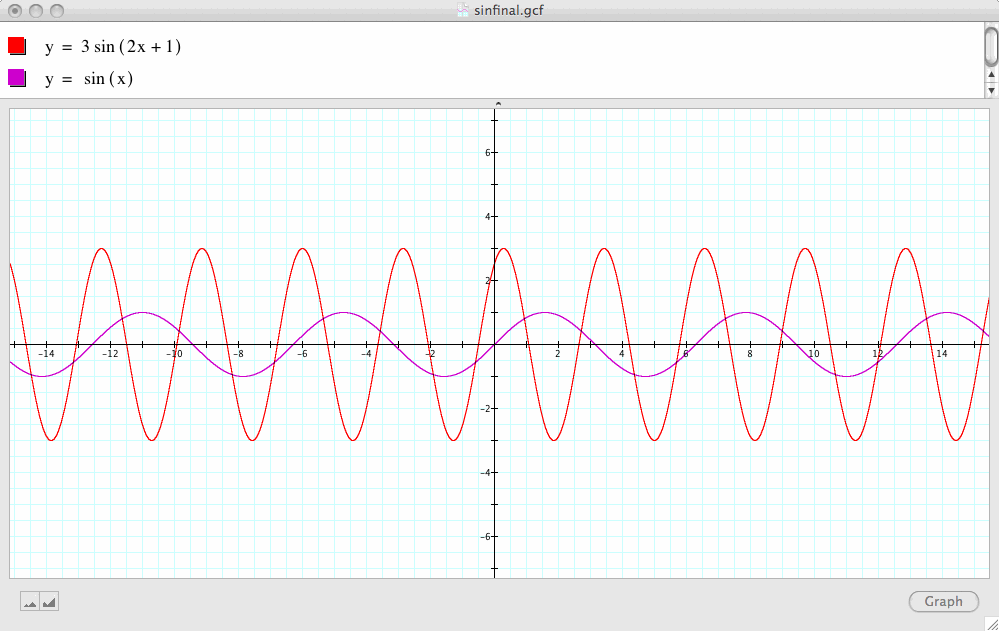
The Problem: Find domain, range, period, and phase shift of y=3sin(2x+1)
Use the three conclusions above, we have:
The domain of this sine function is the set of all real numbers
The range is [-3, 3]
One period equals ![]() /(|b|)=
/(|b|)=![]() /2=
/2=![]()
As compared to sin(x), 3sin(2x+1) has a shift of c/b=1/2 units. Since -1/2<0, the shift is to the left and the magnitude of phase shift is 1/2 units.
Check the following graph and see how well you did :-))