

Assignment XI: "N-leaf" Rose
by
Rui Kang
In this investigation, we look at the equation
![]()
Note:
(1) We only look at the case when a and b are equal, and k is an integer. This is one textbook version of the "n-leaf rose",
(2) Then, we compare the above equation with
![]()
for various k.
(3) Finally, we examine what if ...co() is replaced with sin()?
(1) First, let's fix a=b=1, and let k=1, we obtain a one-leave rose shown below:
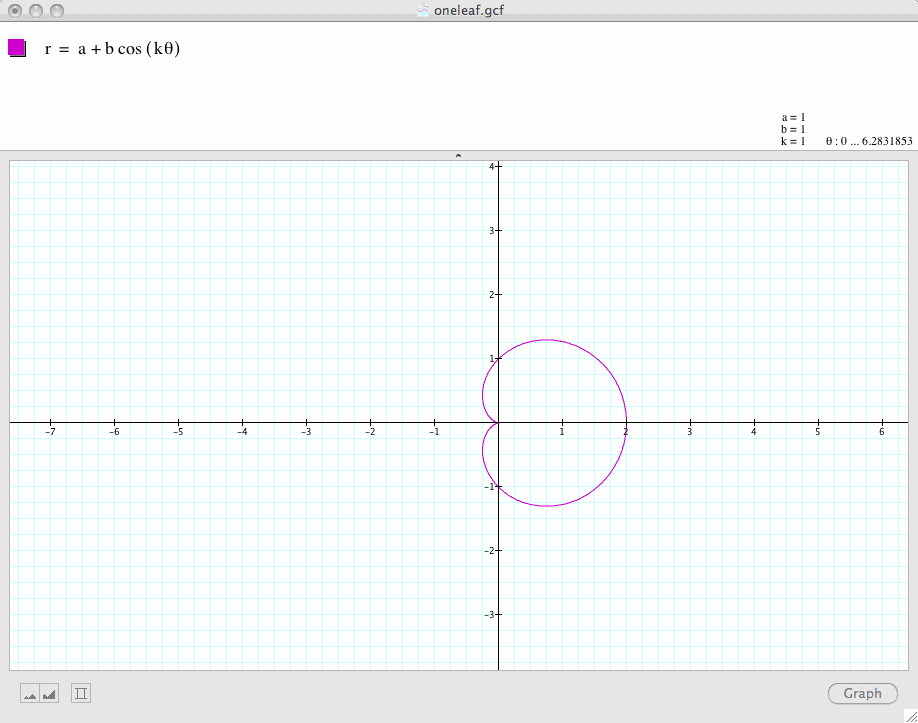
By changing the values of a and b, we find that as long as a=b, no matter what value they take, the graph remains a one-leaf rose except that the size of the rose changes.
Since this investigation mainly concerns the shape of the graph, in the following investigations, we fix a, b at 1.
Next, let's change the value of k, let's k=2, 3, 4, 5
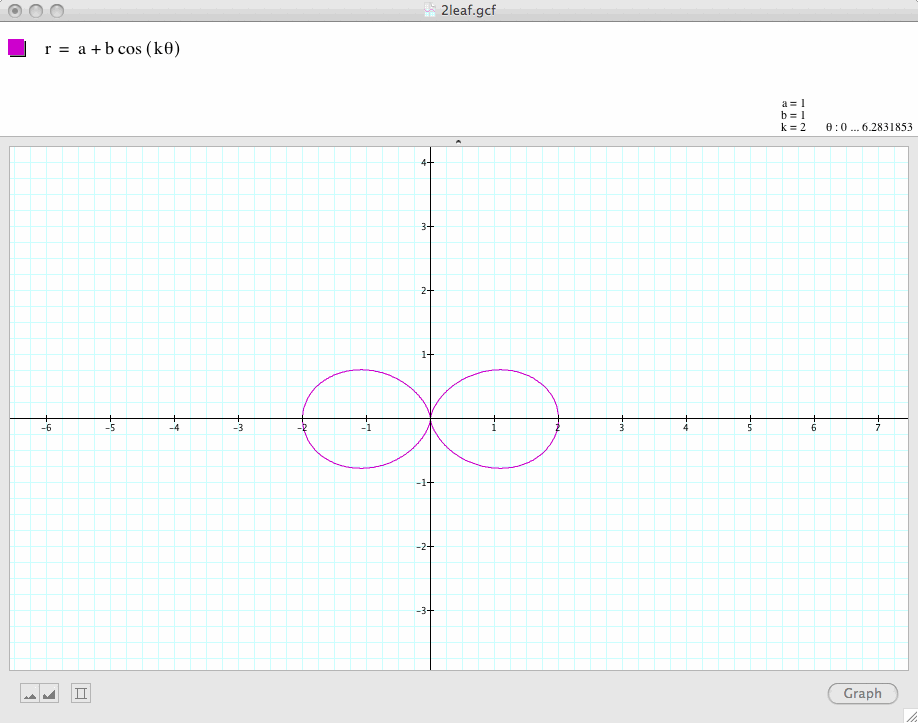
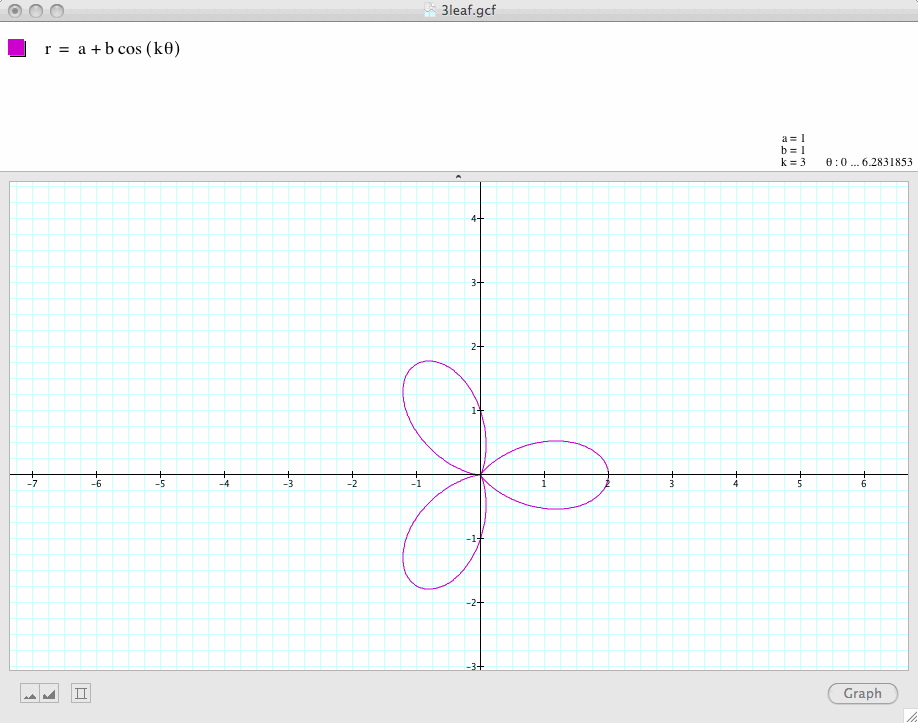
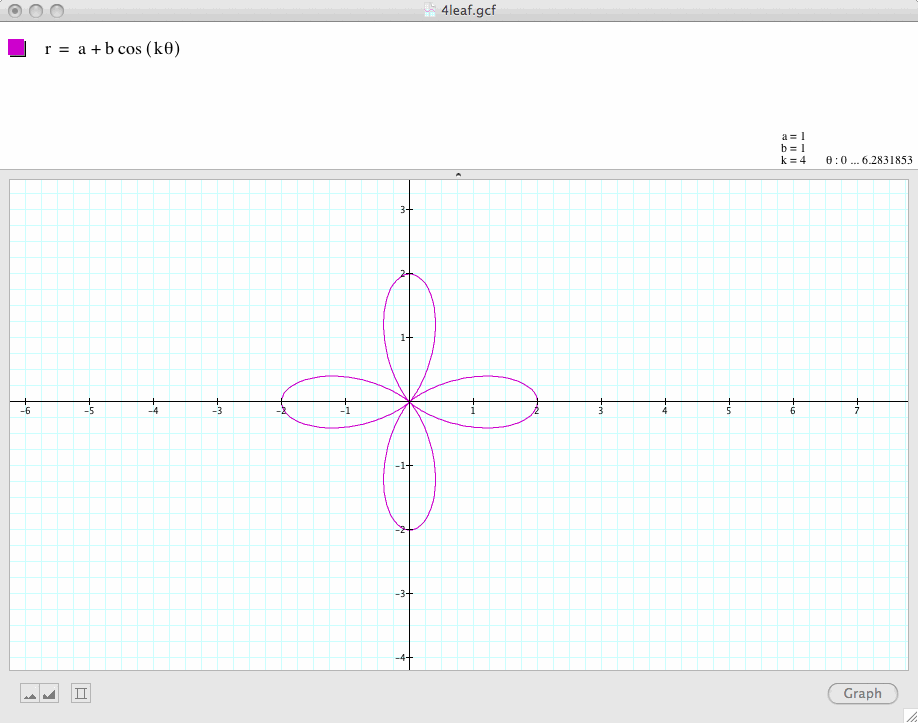
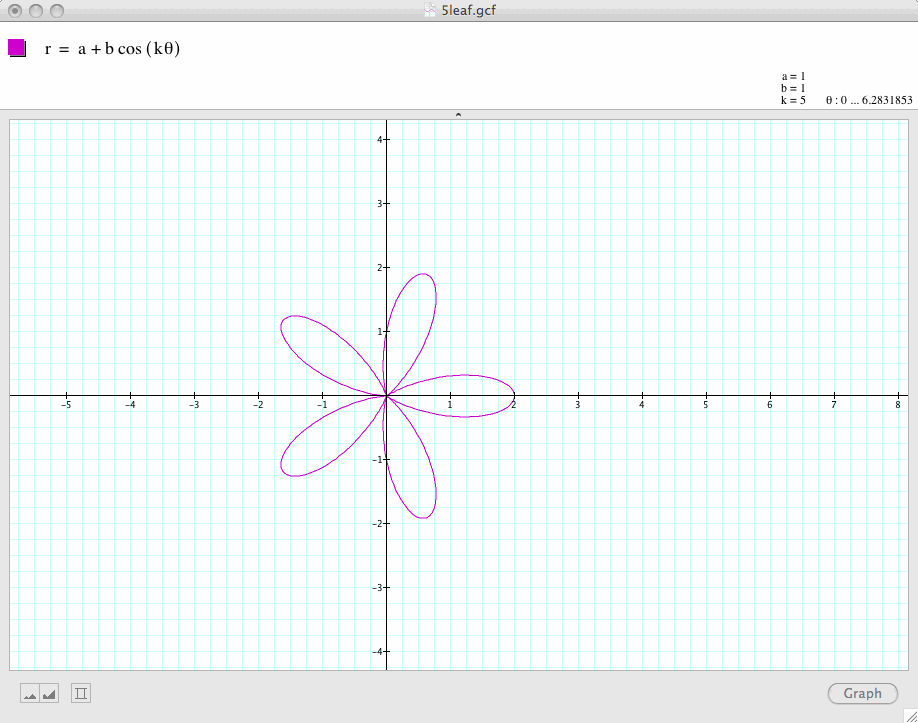
Conclusion 1: In general, if a and b are equal and k is a positive integer, the graph of
![]()
is a k-leaf rose which is symmetric with respect to the x-axis.
If k is even, then the graph is symmetric with respect to both the x-axis and the y-axis. If k is odd, the graph is symmetric with respect to only the x-axis.
The next question is then what happens if k is a negative number or zero?
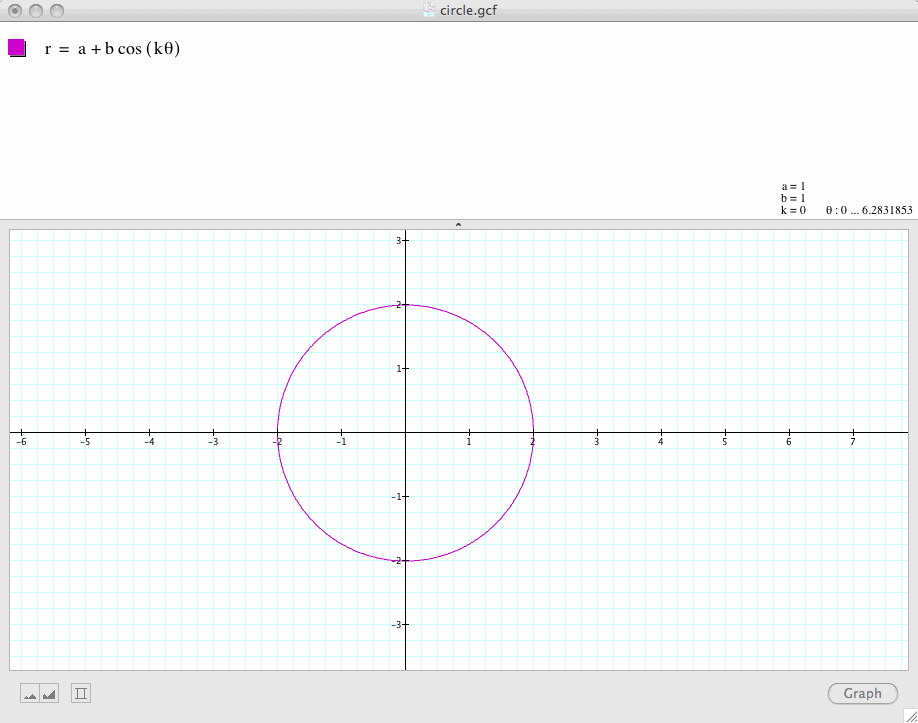
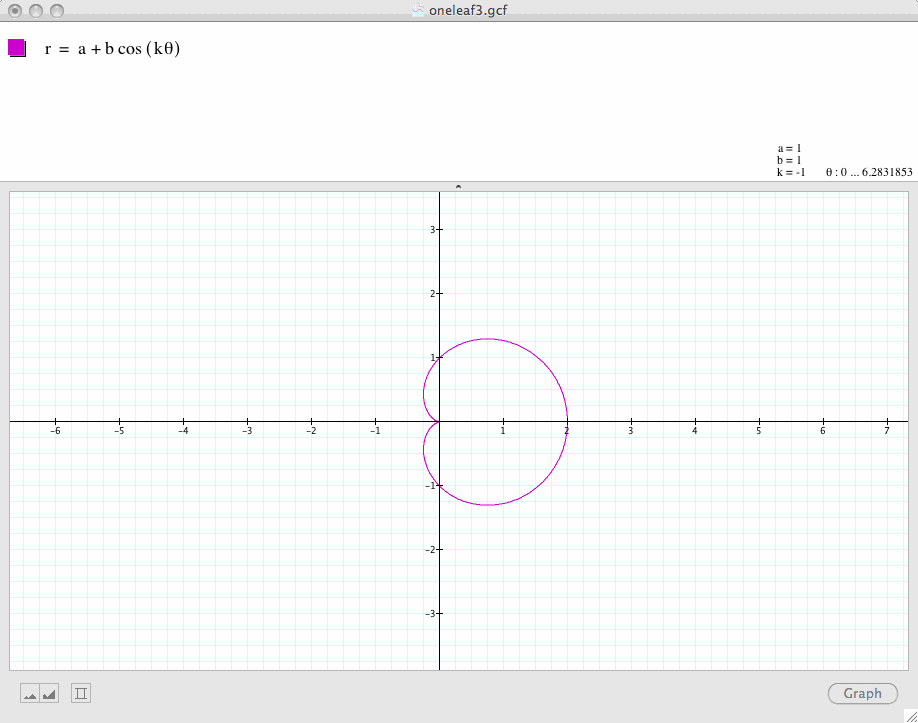
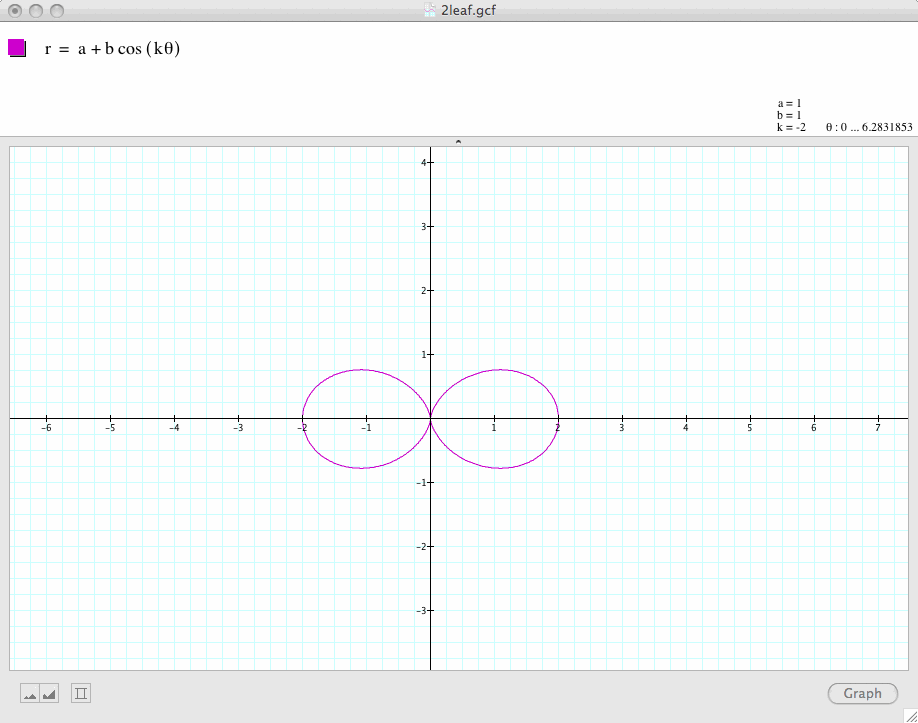
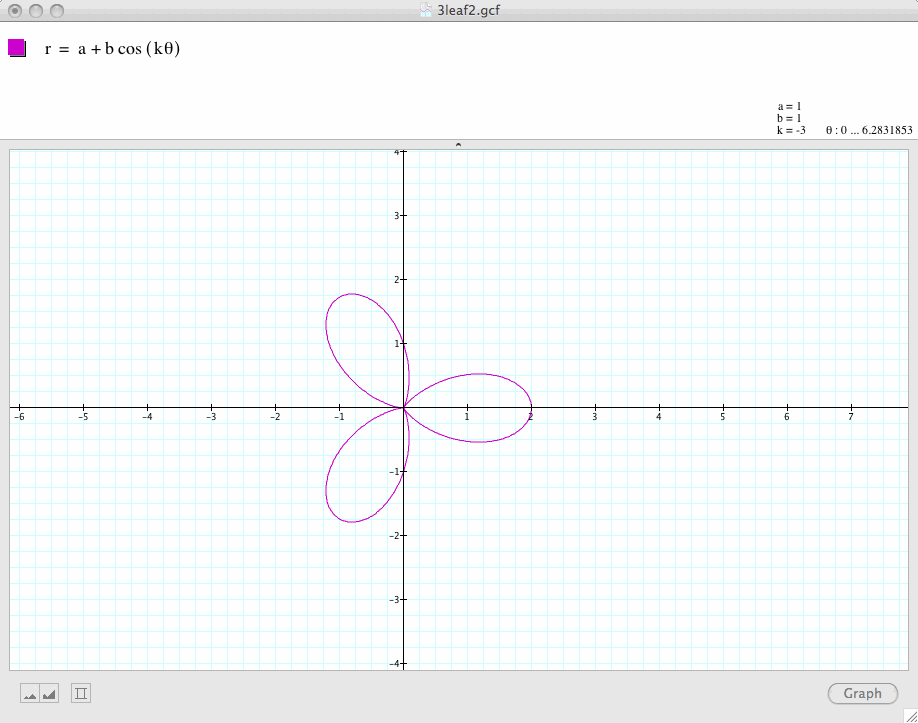
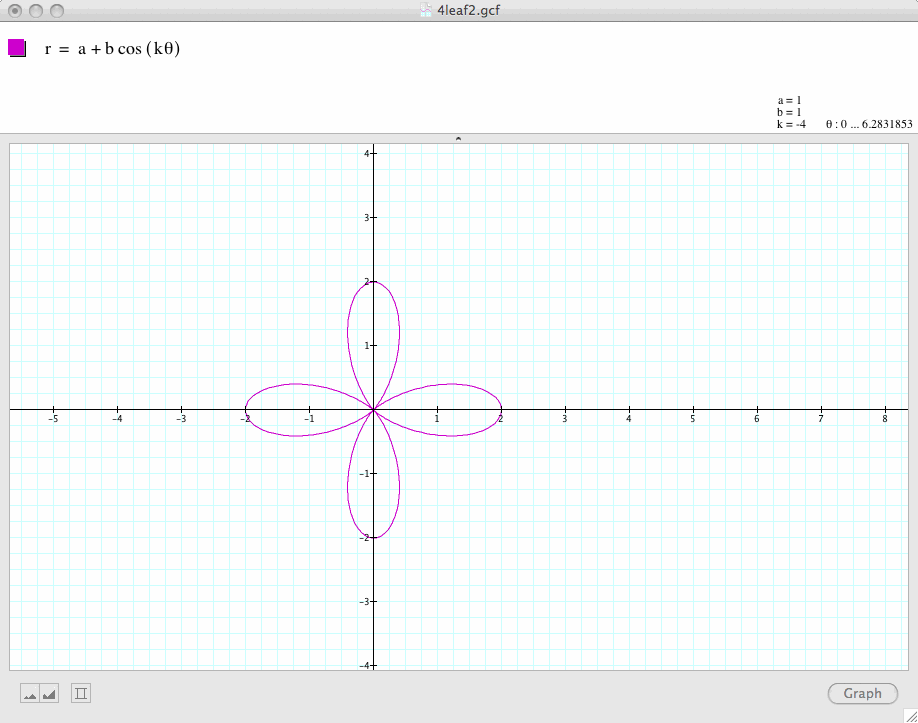
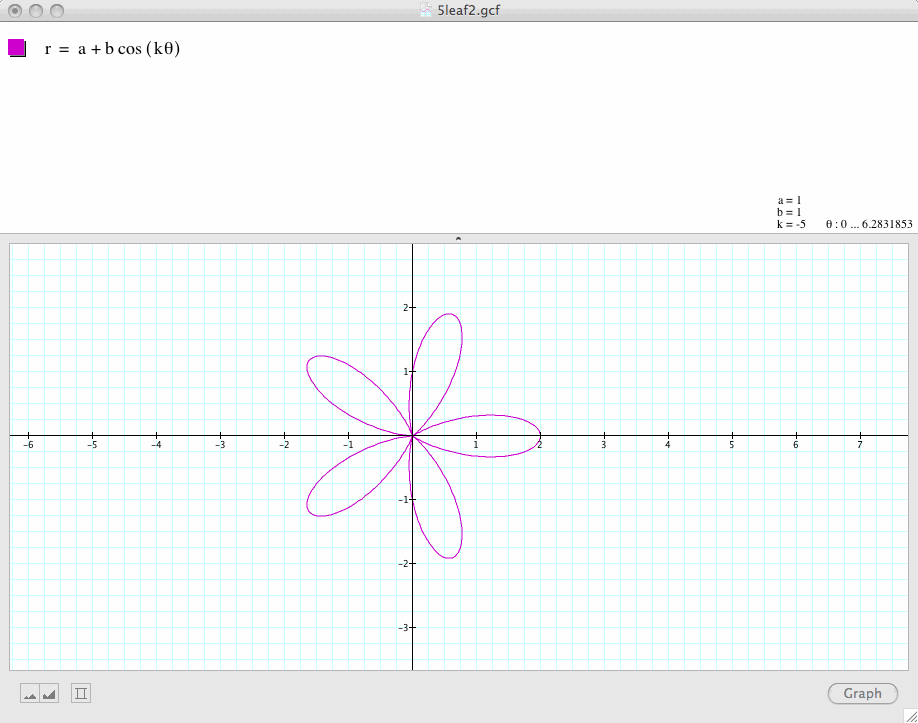
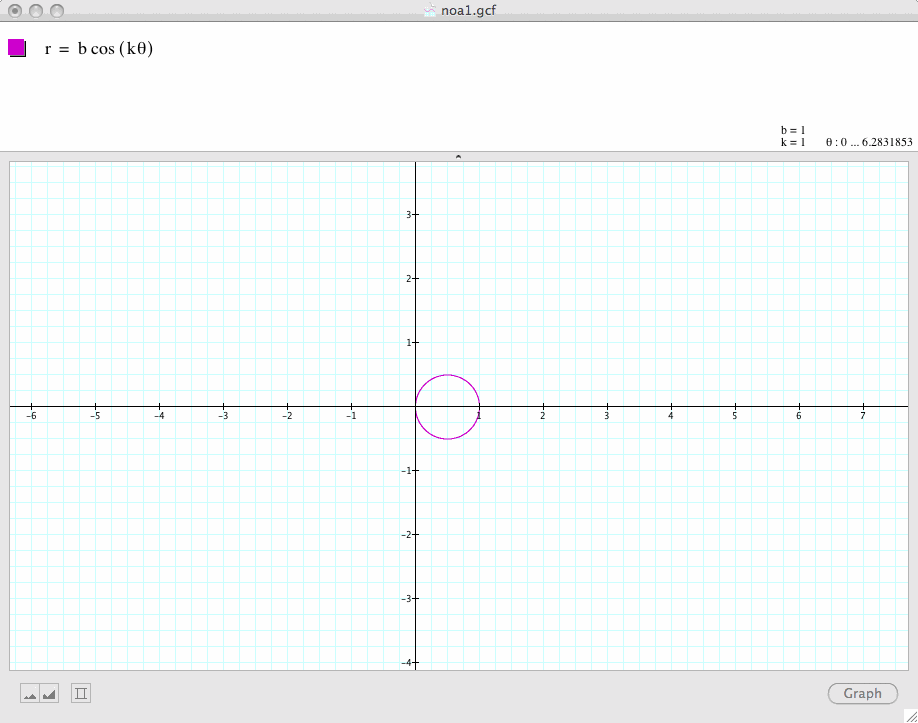
Conclusion 2: When k=0, the graph is a circle.
When k is an negative number, the graph remains that same as those when k is a positive number.
For example, when k = -5, the graph is the same as when k=5. When k=-2, the graph is the same as when k=2.
Note that this conclusion should not suprise us because we know that
![]()
(2) Now we are ready to compare the two polar equations:
![]()
and
![]()
We let k takes on values from 1 to 5 as we did above.
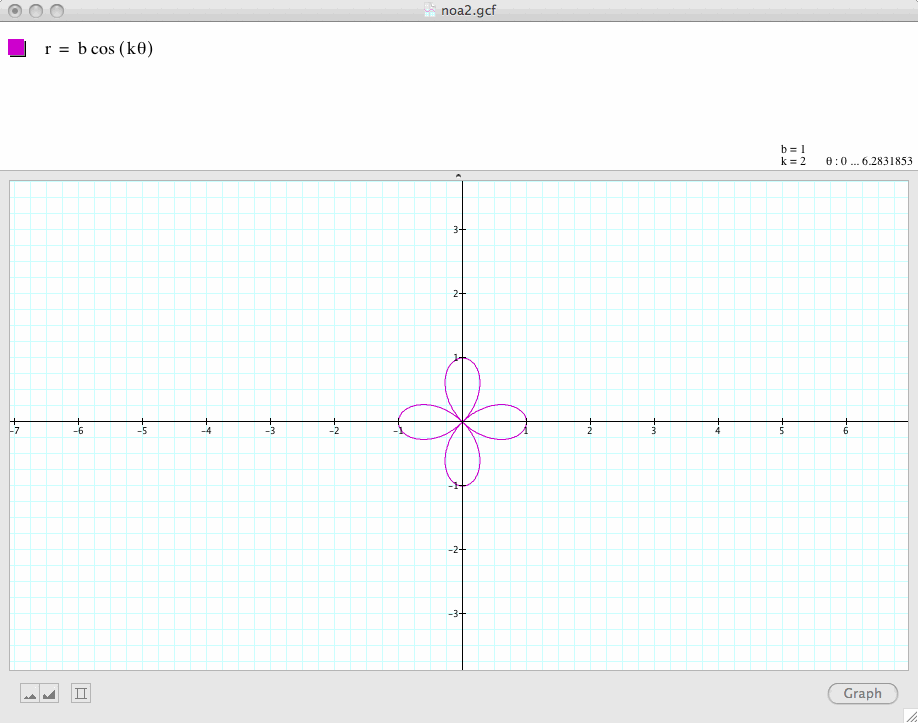
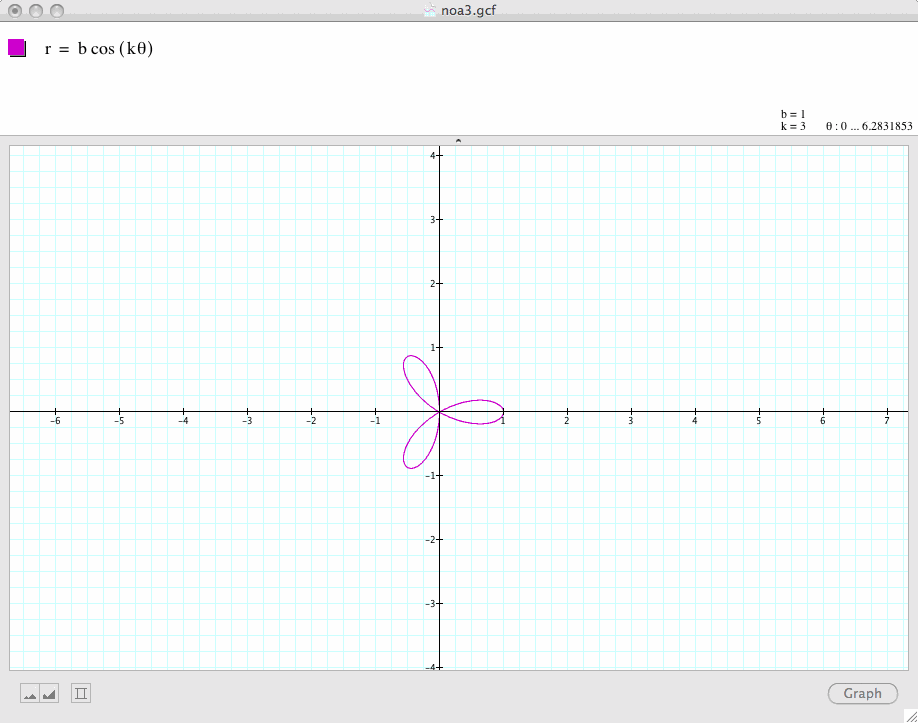
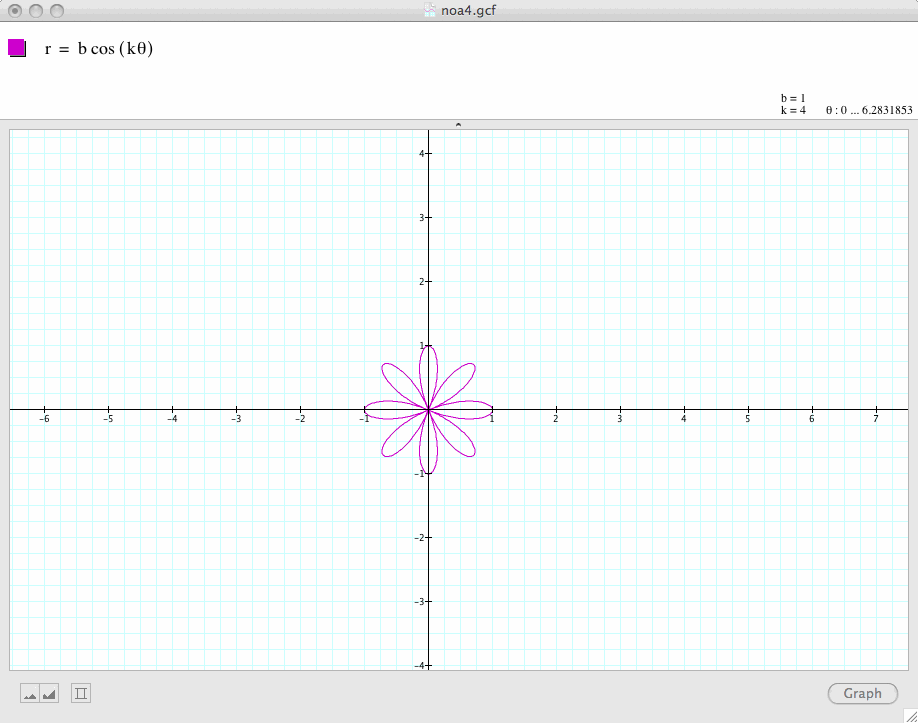
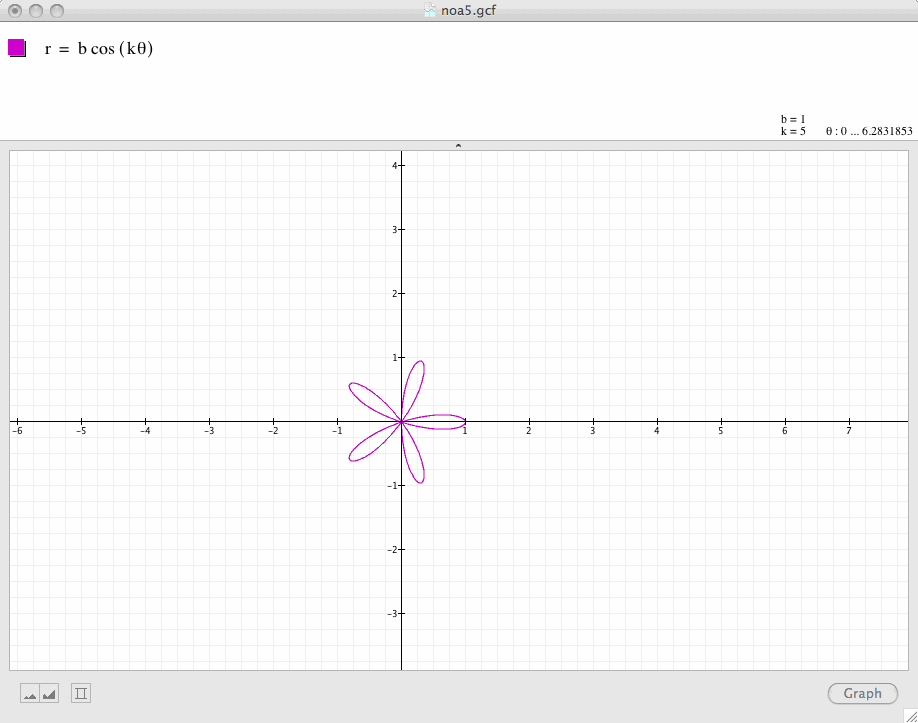
Conclusion 3: The graph of
![]()
is a k-leaf rose when k is odd;
however, when k is even, the graph of
![]()
is a 2k-leaf rose.
In comparison to the graphs of
![]() ,
,
when k is odd, the graphs of the two polar equations are of the same shape.
When k is even, the graphs of
![]()
have twice as many rose leaves as those of
![]() .
.
(3) Finally, we are ready to investigate what happens if we change cos in the equations to sin?
We first try to compare
![]()
and
![]()
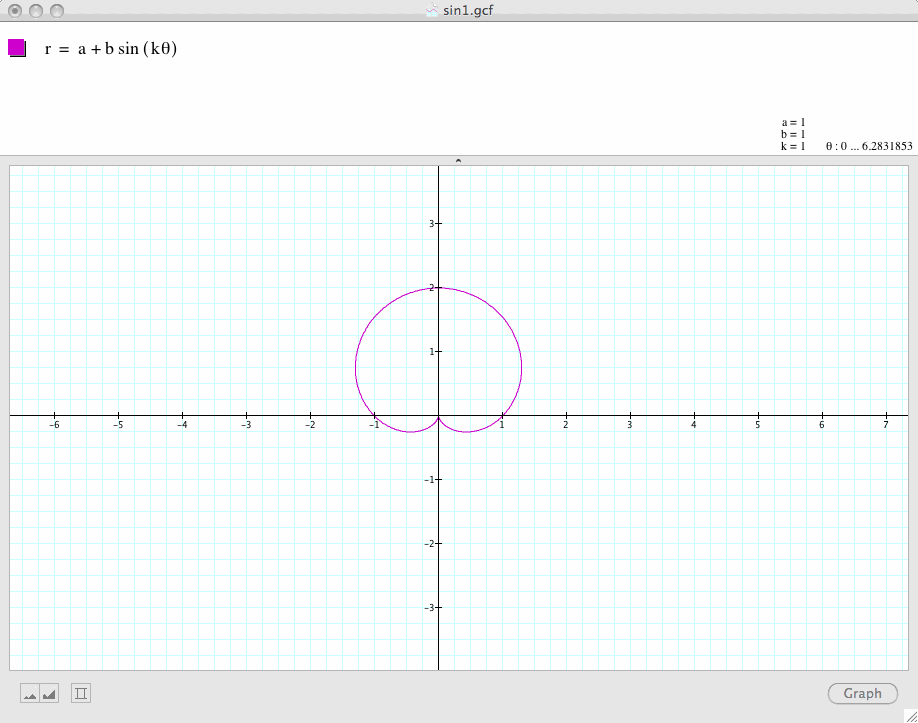
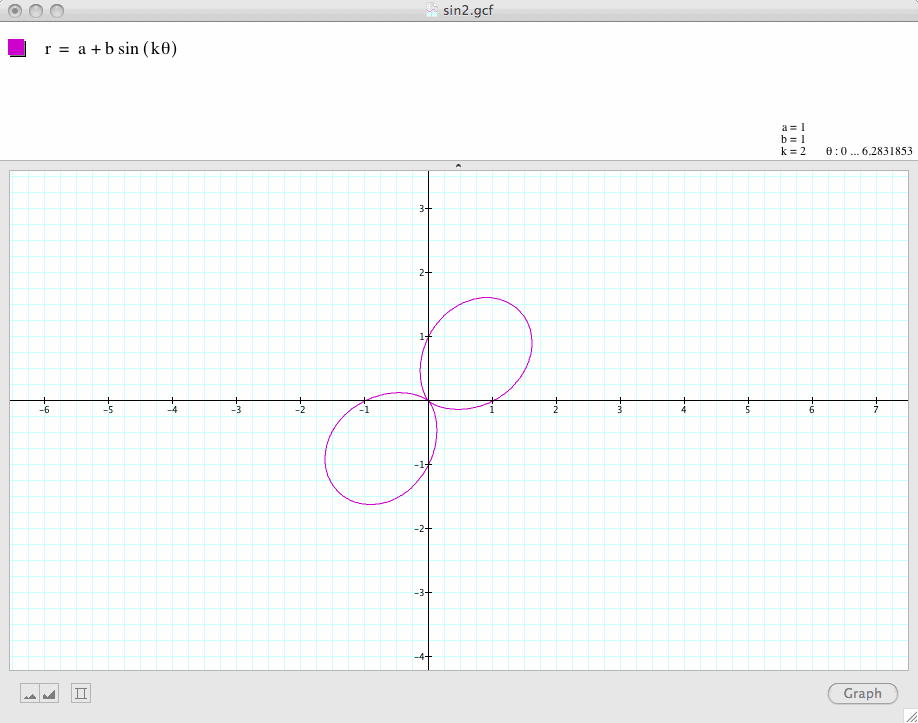
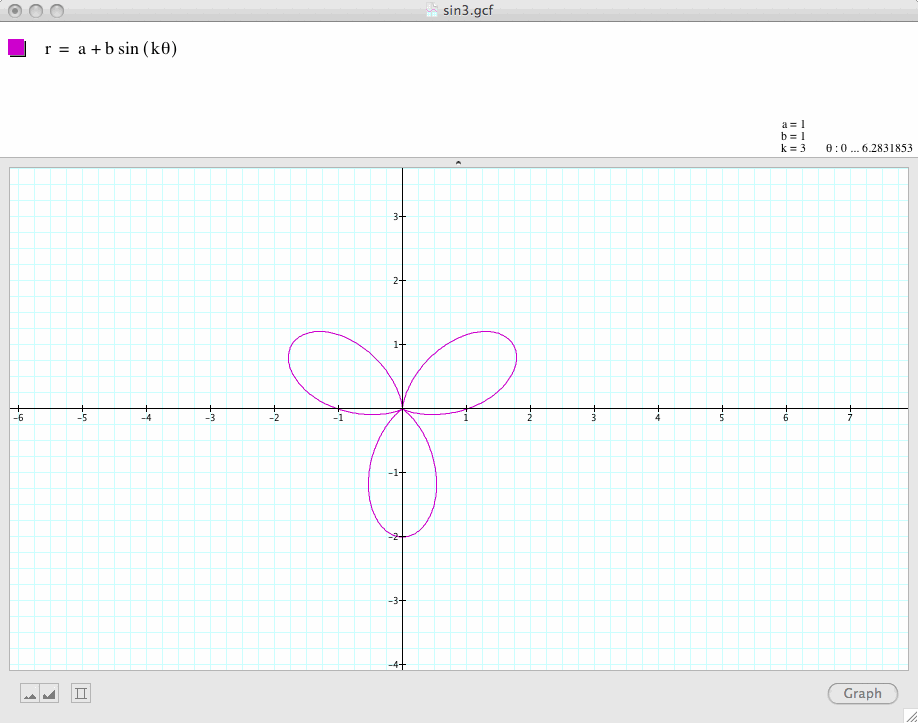
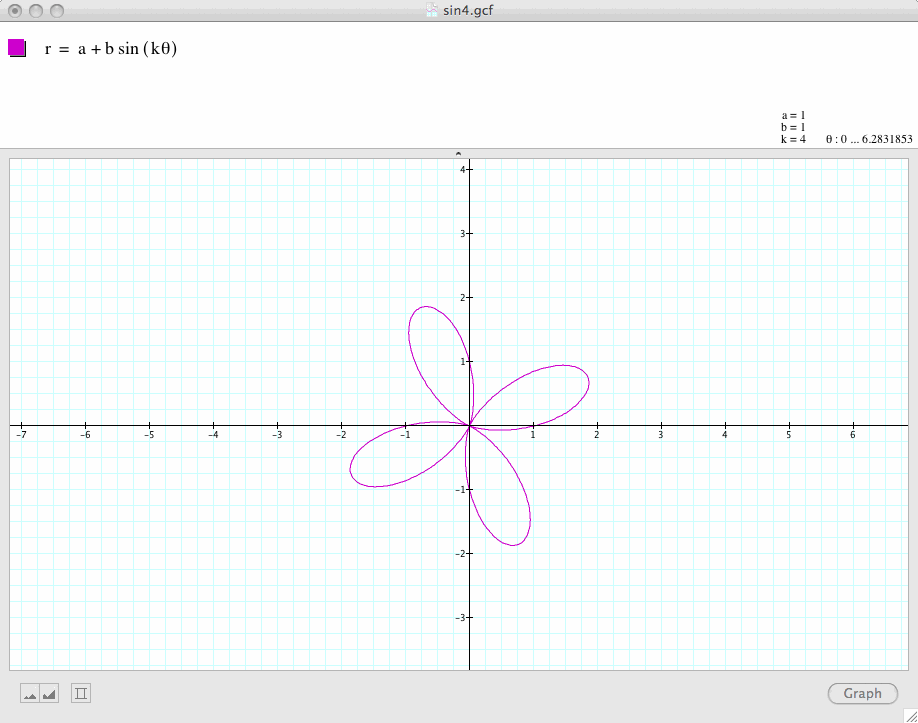
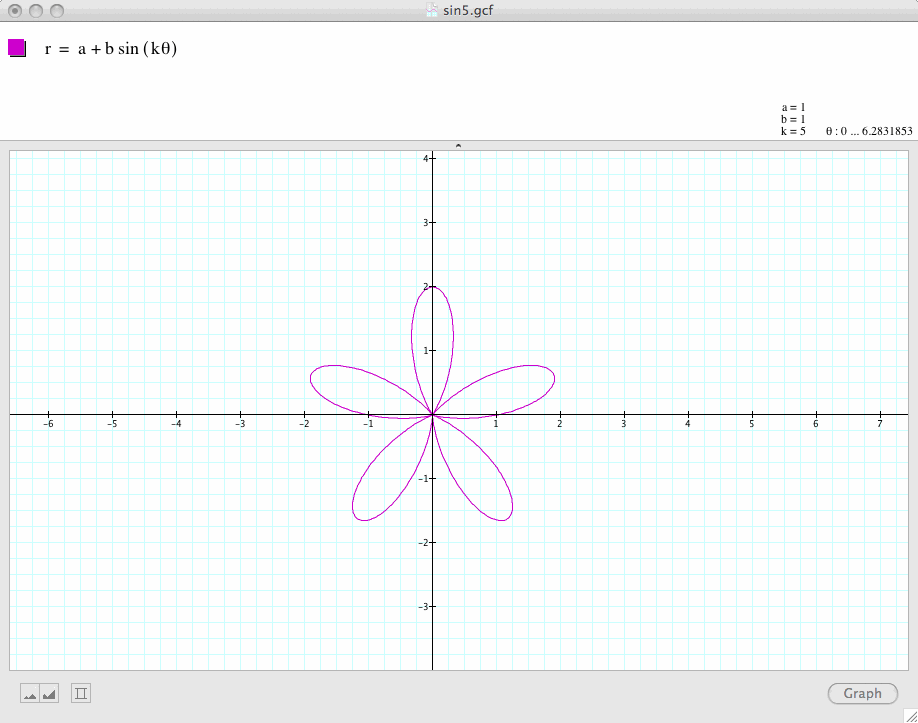
Conclusion 4:
![]()
is also a k-leaf rose, and in fact, if we rotate the graph of
![]()
by a certain degree, we will get
![]() .
.
Regardless of the value of k, the graphs for these two polar equations are always congruent despite the fact that their leaves point to different directions.
We now try to compare
![]()
and
![]()
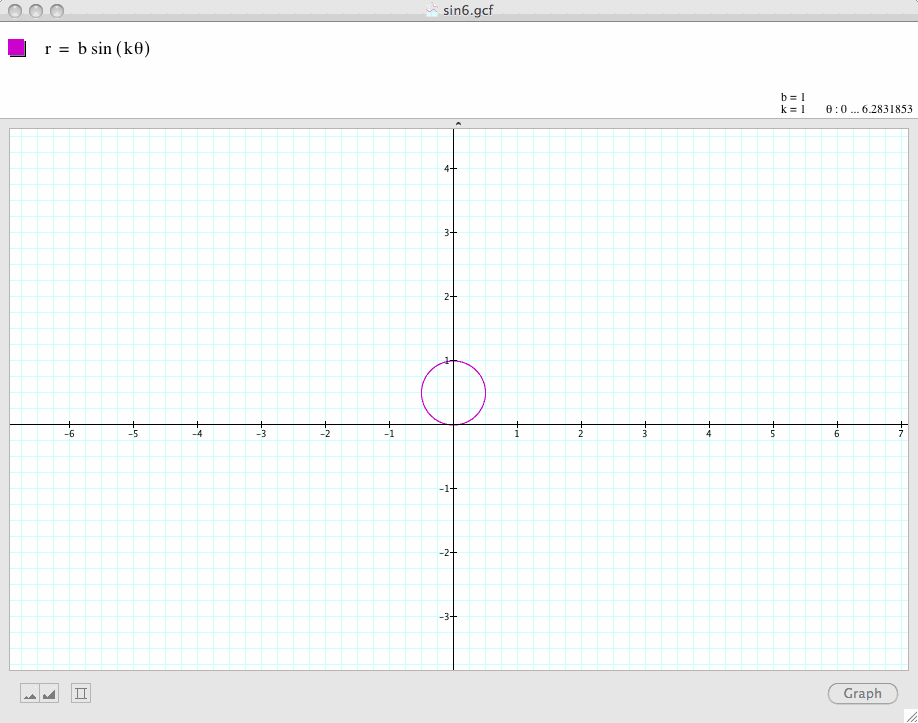
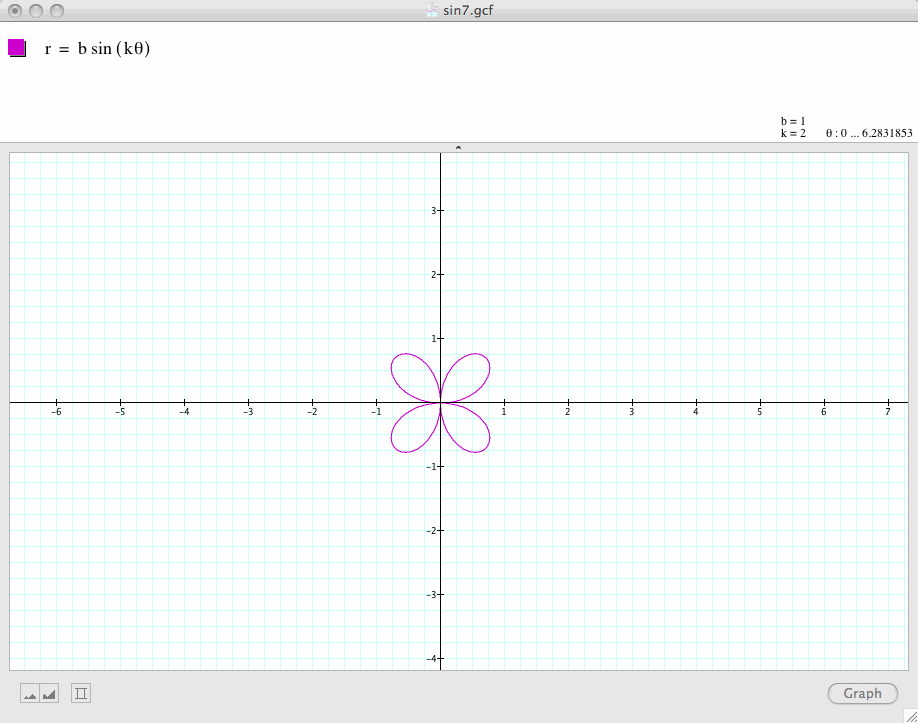
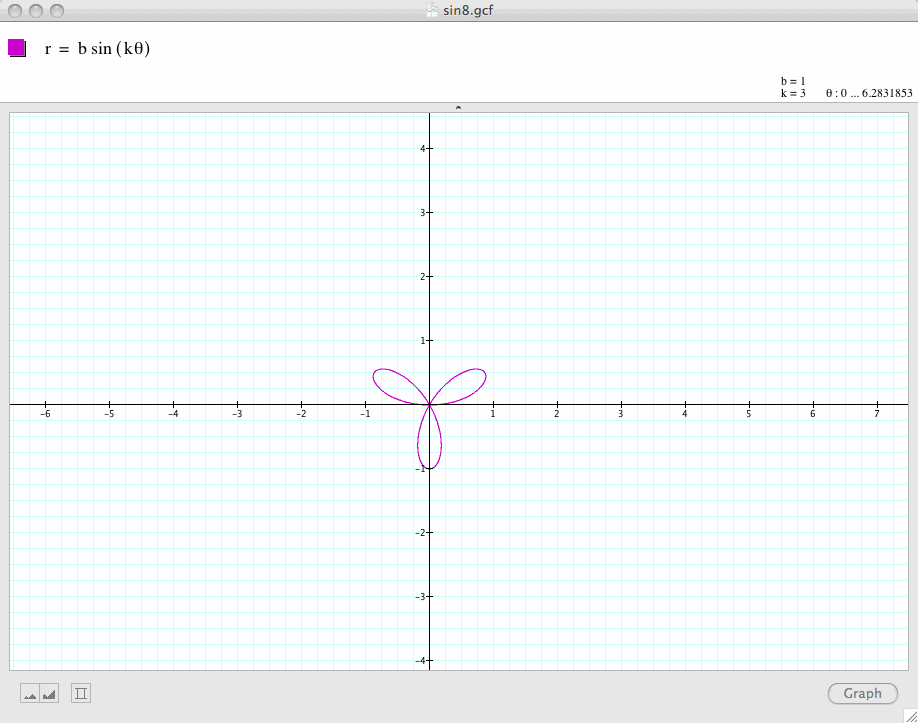
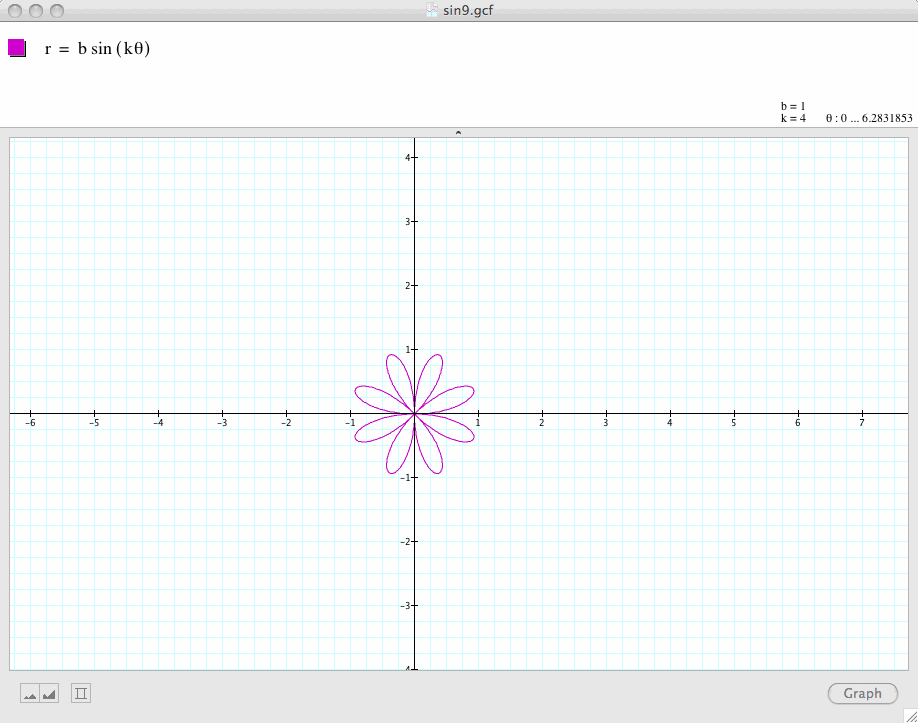
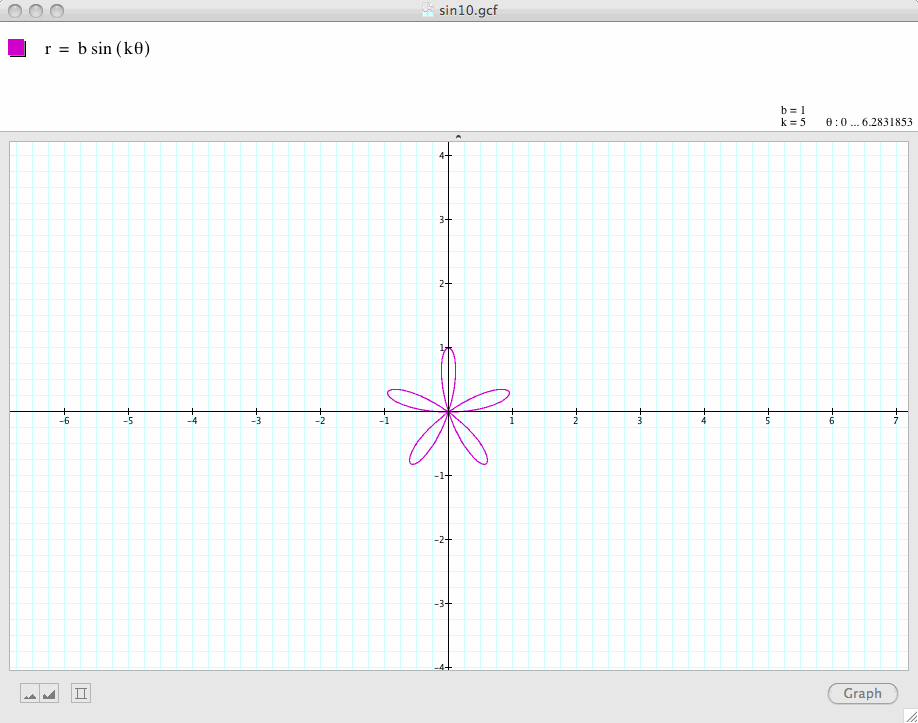
Conclusion 5: By examininh the above set of graphs, we find that
![]()
is a k-leaf rose when k is odd, and a 2k-leaf rose when k is even.
In addition, if we roate the corresponding graph of
![]() by a certain degree, we will get
by a certain degree, we will get
![]() and vice versa.
and vice versa.
Regardless of the value of k, the graphs for these two polar equations are always congruent despite the fact that their leaves point to different directions.