Assignment XII: Fibonacci Sequence
by
Rui Kang
Generate a Fibonacci sequence in the first column using f(0)=1, f(1)=1, and
f(n)=f(n-1)+f(n-2)
a. Construct the ratio of each pair of adjacent terms in the Fibonacci sequence.
What happens as n increases? What about the ratio of every second term? etc.
The story behind Fibonnaci Sequence:
Medieval mathematician and businessman Fibonacci (Leonardo Pisano) posed the following problem in 1202:
How many pairs of rabbits will be produced in a year, beginning with a single pair,
if in every month each pair bears a new pair which becomes productive from the second month on?
It is easy to see that 1 pair will be produced the first month, and 1 pair also in the second month (since the new pair produced in the first month is not yet mature),
and in the third month 2 pairs will be produced, one by the original pair and one by the pair which was produced in the first month.
In the fourth month 3 pairs will be produced, and in the fifth month 5 pairs.
After these things expand rapidly, and we get the following sequence of numbers:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,...
This is an example of a recursive sequence, obeying the simple rule that to calculate the next term one simply sums the preceding two:
f(1)=1
f(2)=1
f(n)=f(n-1) + f(n-2)
Thus 1 and 1 are 2, 1 and 2 are 3, 2 and 3 are 5 and so on.
The above materials is retrieved July 12, 2009 from http://www.mathacademy.com/pr/prime/articles/fibonac/index.asp
Now let's look at an Excel-generated Fibonacci Sequence following the above rule:
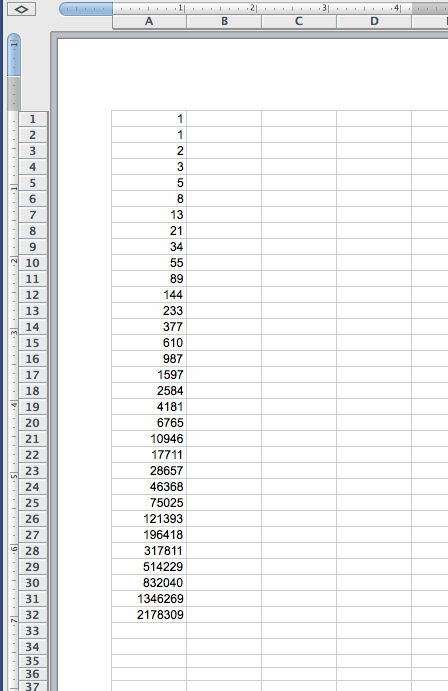
Now let's construct the ratio of each pair of adjacent terms in the Fibonacci sequence as the following:
a(0) = 1/1, a(1) = 2/1, a(n) = 
This gives us a new sequence:
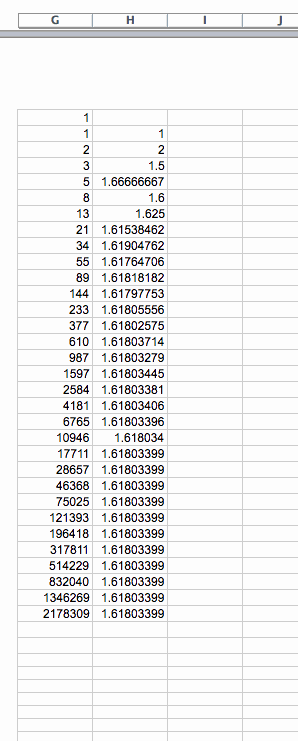
As we observe this sequence,
we find that although the first several values oscillate up and down, very quickly the sequence approaches to a value close to 1.618034.
In fact, this value is called the Golden Ratio. We may find the exact value of the golden ratio using two methods:
Method 1:
We know by the definition of Fibonacci Sequence that:
Method 2: Next let's try to understand and express the exact Golden Ratio using a geometric method. Observe the following triangle:
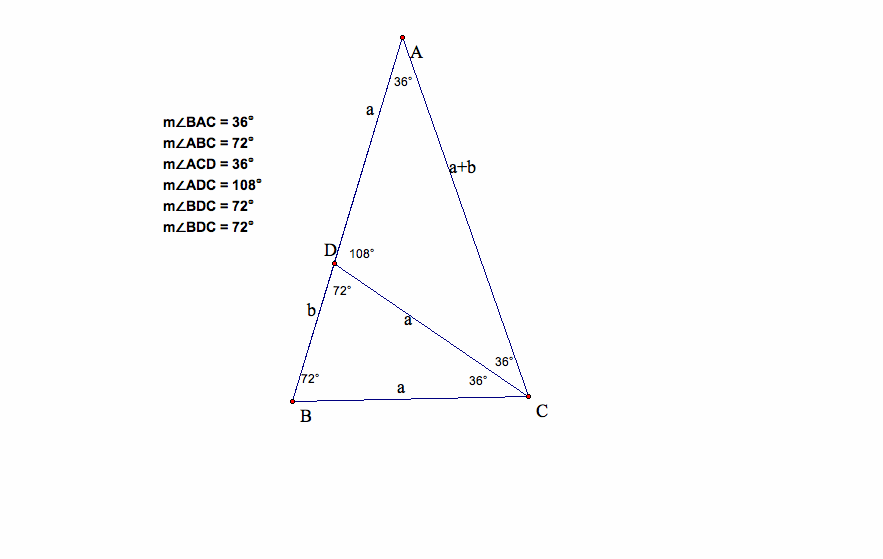
So far, we have considered the ratio of each pair of adjacent terms in the Fibonnaci sequence, but how about sequence
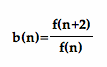, i.e., the ratios between every second terms?
i.e., b(0) = 2/1, b(1) = 3/1, b(2)=5/2,
:
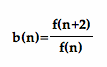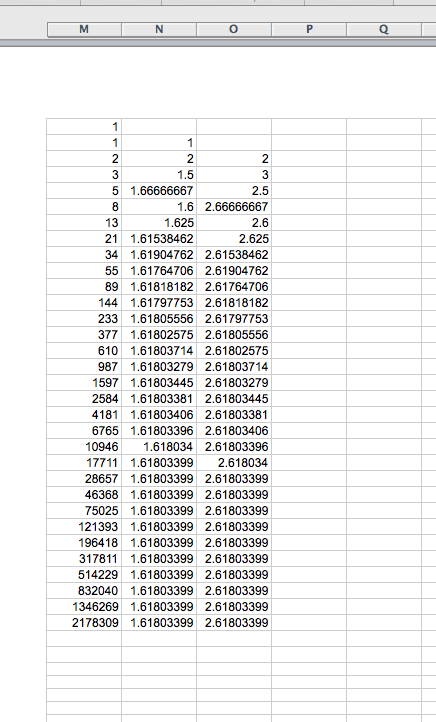
Here we observe that the sequence b(n) also converges to a number, in fact, close to 2.618034 or 1 plus the Golden Ratio!
In fact, this observation can be easily proved mathematically:
Now let's continue our investigation to
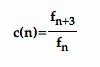, hopefully we will find some relations that we eventually may generalize to all such sequences:
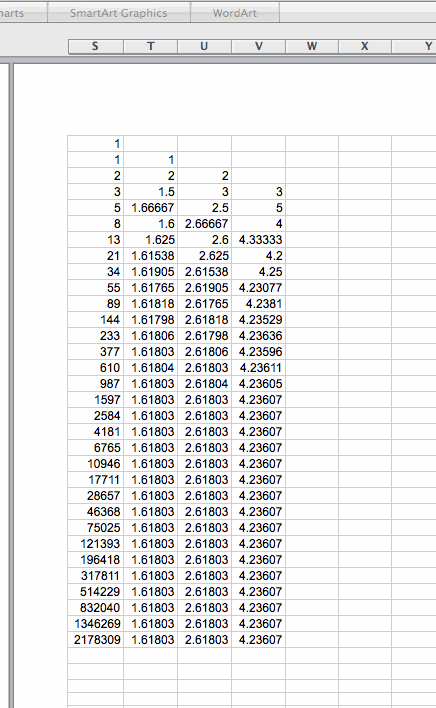
This time we observe that c(n) also approaches a number, close to 4.23608,
and the behavior of this sequence is highly similar to the previous sequences.
But what is the relationship between this number 4.23608 and the Golden Ratio?
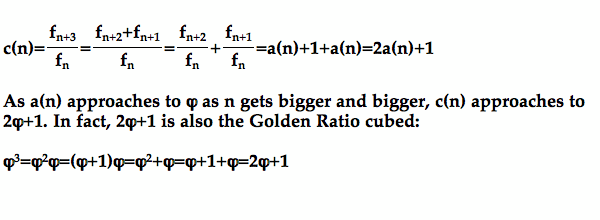
Let's investigate one more sequence and then we will see whether we get generalize our results to all such upcoming sequences:
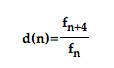
We notice that d(n) also converges to a number pretty much like our earlier sequences. This time the number is 6.854102.
Based on our experience so far, we may guess that this number can also be expressed by the Golden Ratio like:
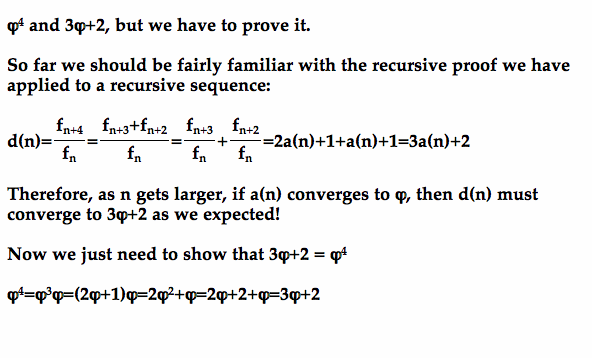
Conclusion 1:
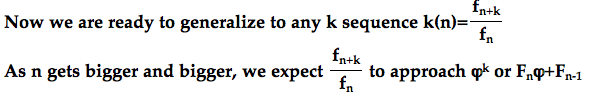
b. Explore sequences where f(0) and f(1) are some arbitrary integers other than 1. If f(0)=1 and f(1)=3, then your sequence is a Lucas Sequence.
All such sequences, however, have the same limit of the ratio of successive terms.
In the second part of this investigation, we want to see whether the two starting values affect the limit of the ratio of successive terms.
First, let's look at what happens if we change f(0)=1 and f(1)=3?
This sequence in fact is not a Fibonaaci Sequence anymore. It is called a Lucas Sequence:
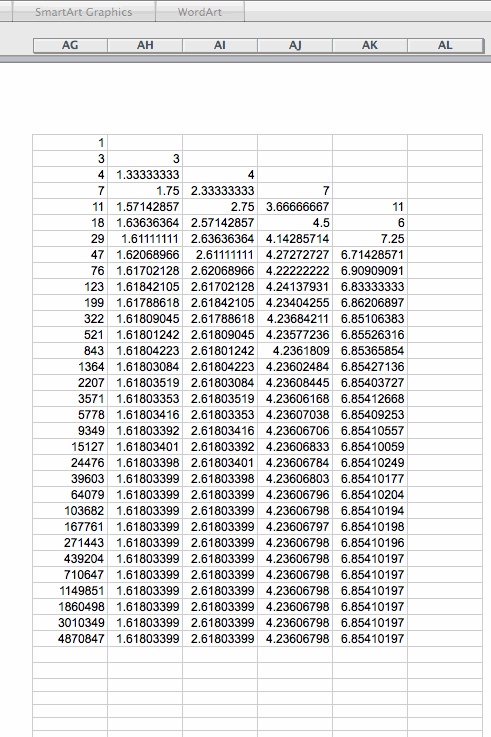
We find that the change from f(1) = 1 to f(1) = 3 did not affect the limit of the ratio of successive terms.
Let's try some other numbers, you may ask what happens if the first number is larger than the second number, will that matter?
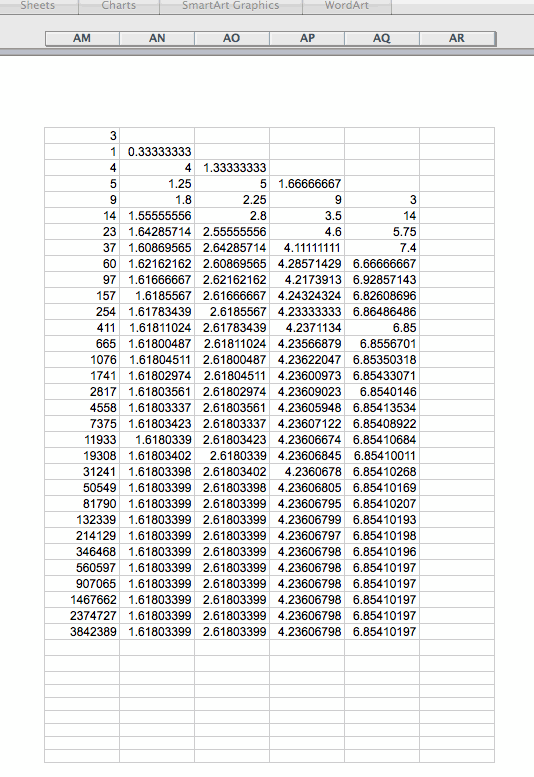
Our observation is that it doesn't matter!
The limit of the ratio of successive terms still approaches to the same number as in the Fibonacci sequence!
How about we start from 0? Let's look at the next example:
Again it doesn't matter!
Even if we start our sequence with 0, the limit of the ratio of successive terms still approaches to the same number as in the Fibonacci sequence!
Conclusion 2: In fact, except for the case when both of our starting values are zeros,
the initial values of all such sequences does not affect the limit of the ratio of successive terms.
If you are really a skeptical person and say what happens if we start with negative values, with fractions?
Check the following two examples and see if you are convinced!
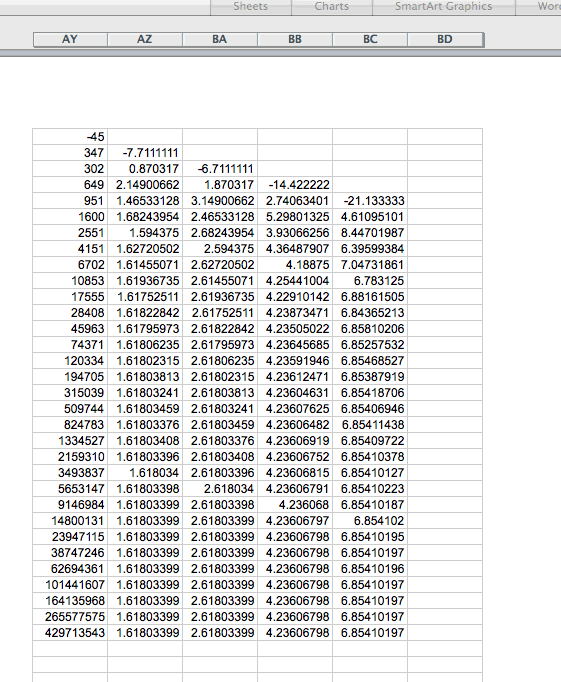
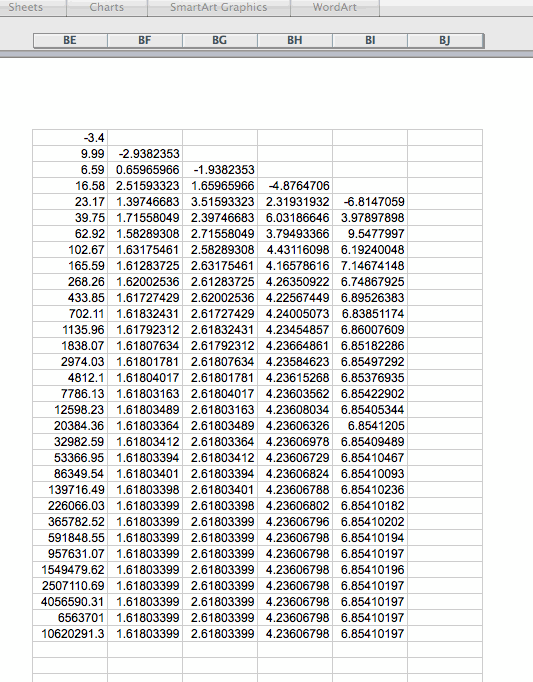
Big conclusion: I believe it is fairly safe to say that the initial values of all such sequences do not affect the limit of the ratio of successive terms!
In other words, all such sequences will eventually converge to the same set of values, all related to the Golden Ratio.
If you want to explore this investigation yourself, you may want to check out this excel file first. Good Luck!