Assignment IV: Circumcenter of a Triangle
by
Rui Kang
In this investigation, we examine the circumcenter (C) of a triangle.
In particular, we look at the definition of a circumcenter and how it is related to a circumcirlce.
What is a circumcenter and how is it constructed?
The circumcenter (C) of a triangle is the point in the plane equidistant from the three vertices of the triangle.
Since a point that is equiditant from two points lies on the perpendicular bisector of the segment determined by the two points,
C is on the perpendicular bisector of each side of the triangle.
This tells us how to construct the circumcenter (C) when given any arbitrary triangle
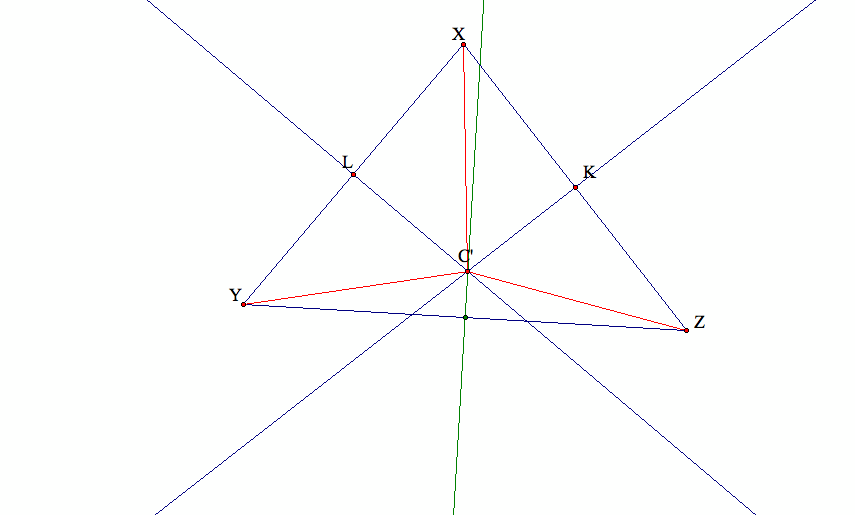
Here is a step-by-step construction of the circumcenter (C):
(1) Construct an arbitrary triangle XYZ,
(2) Construct the midpoint of each of the sides of the triangle: K, L, and M,
(3) Now we are ready to draw the perpendicular lines that passes through K, L, M
and are perpendicular to XZ, YZ, and XY respectively,
(4) Now we note that these three perpendicular bisectors (in dashed blue) do intersect at one point,
and this point is the circumcenter C.
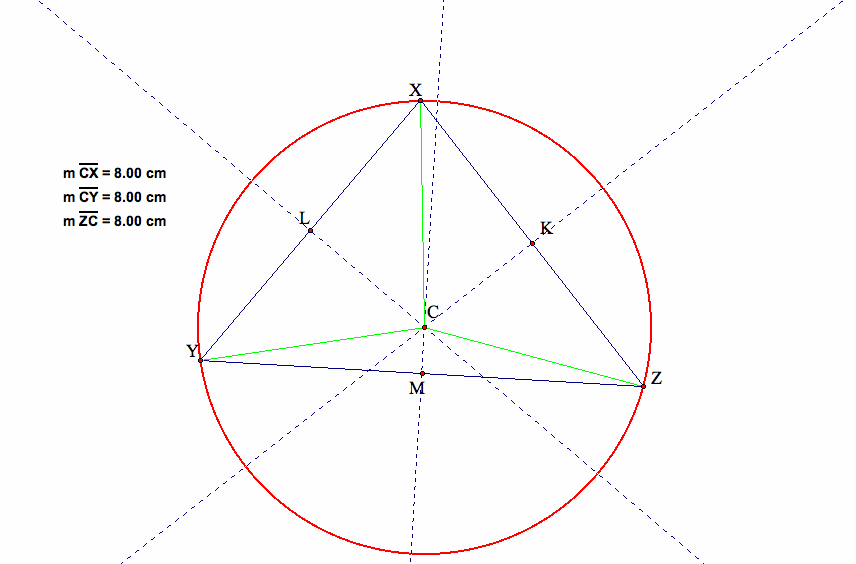
To test that C is indeed of equidistance from the three vertices of the original triangle XYZ,
if we connect XC, YC, and ZC and measure these three segments, this shows that indeed
|XC|=|YC|=|ZC|. (Note: On this website, I use | | to express the length of a segment unless otherwise indicated)
Now we are ready to draw the circumcircle of the triangle. Select C and any of the vertices of triangle XYZ, say, X,
we create a circle (in red), and we observe that this circle passes all three vertices of XYZ.
A side note: The circumcenter (C) can be outside of a triangle as shown below:
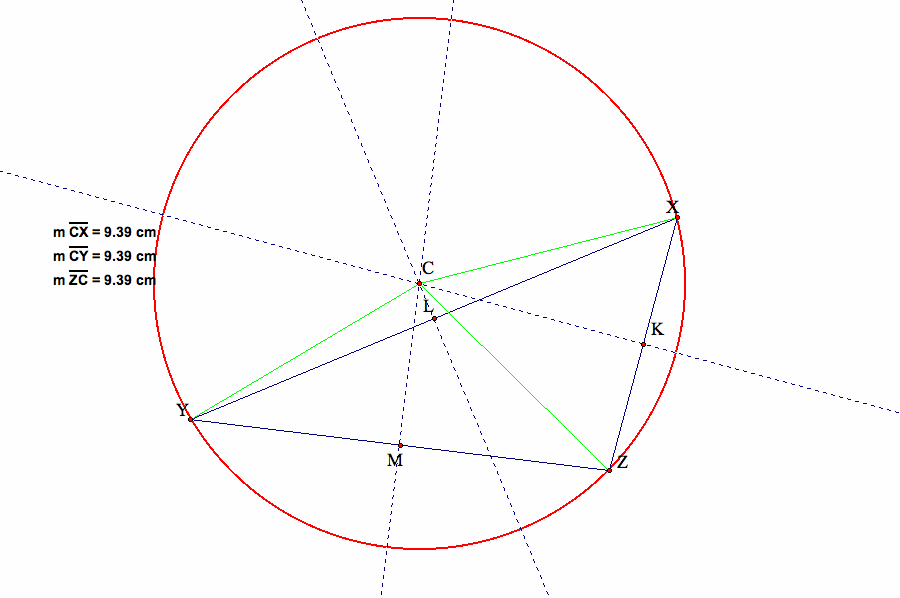
But now we may ask the question, will the three perpendicular bisectors of any arbitrary triangle always concurrent?
In other words, can we prove that the three perpendicular bisectors (hereinafter abbreviated as PB) always intersect at one point?
The Proof:
(Refer to the graph below)
We start this proof by drawing two PBs first.
Let's draw the PB of XZ and then PB of XY and these two PBs must intersect at one point, let's call it C'.
Our task is to show that the PB of the third side YZ also will pass this C',
and then we are confident to say that this C' is indeed C, the circumcenter of the triangle.
First, let's connect C'X, C'Y, and C'Z.
We note that since C' lies on the PB of XZ, then |C'X|=|C'Z|.
Similarly, since C' lies on the PB of XY, then |C'X)=|C'Y|.
But this means that |C'Y|=|C'Z|.
Finally, by the definition of PB, we know that C' must lie on the PB of YZ.
In other words, the PB of YZ passes C' as required,
i.e., C' is the intersection of three PBs of triangle XYZ, and the intersection is precisely triangle XYZ's circumcenter.
Thus we have proved that the three PBs of any arbitrary triangle must be concurrcent (also see below).