Assignment VIII: Orthocenter of a Triangle
by
Rui Kang
In this investigation, we focus on some of the properties related to the Orthocenter of a triangle. In particular, we proceed with the following:
1. Construct any triangle ABC.
2. Construct the Orthocenter H of triangle ABC.
3. Construct the Orthocenter of triangle HBC.
4. Construct the Orthocenter of triangle HAB.
5. Construct the Orthocenter of triangle HAC.
6. Construct the Circumcircles of triangles ABC, HBC, HAB, and HAC.
7. Conjectures? Proofs?
What would happen if any vertex of the triangle ABC was moved to where the orthocenter H is located?
Where would H then be located?
Recall, an orthocenter of a triangle is the intersection of the three altitudes.
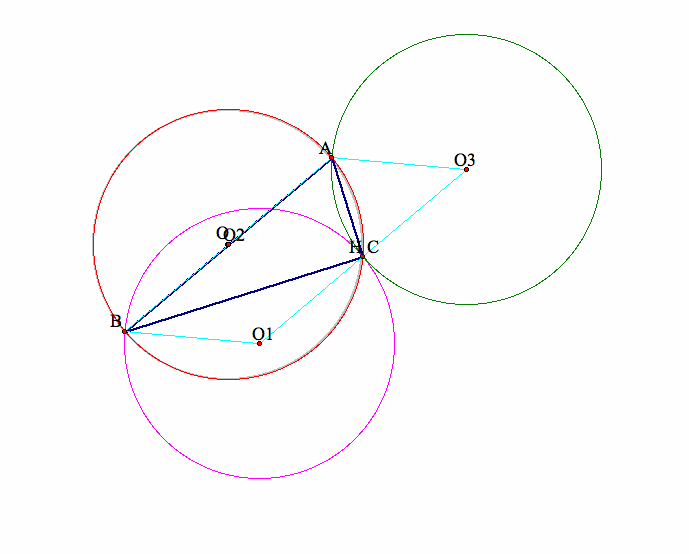
First let's draw any arbitrary triangle ABC. Then we draw the three altitudes of triangle ABC, i.e., AD, BE, and CF.
As expected, they intersect at a point H, then H is the orthocenter of triangle ABC.
Next let's find the orthocenter of triangle HBC. We already have one altitude, that is, HD.
Since we know that the three altitudes of a triangle intersect at one point, we only need to draw another altitude of triangle HBC,
then we will find the orthocenter of triangle HBC.
We decide to draw an altitude from C to BH, and we find that this altitude lies on the same line on which side CA of triangle ABC lies.
In fact, CE is the altitude of triangle HBC from C to BH.
Now we have two altitudes CE and HD. CE lies on the same line that CA lies; HD lies on the same line that AD lies.
In other words, CE and HD intersects at point A, which is one of the vertices of triangle ABC.
So we have found out that in fact, the orthocenter of triangle HBC is simply vertex A of the original triangle ABC!
Similarly, we find that the orthocenter of triangle HAB is vertex C, and the orthocenter of triangle HAC is vertex B.
The next big step of this investigation is to draw the circumcircles of triangles ABC, HBC, HAB, and HAC.
In an earlier investigation for Assignment 4, I have discussed in details what the circumcenter of a triangle is and how it is related to the circumcircle.
If you need to refresh your memory about how to construct a circumcircle, please refer to my Assignment 4.
Suppose we have finished constructing the orthocenters of triangles ABC, HBC, HAB, and HAC, and as well as the circumcircles for the four triangles.
The graph should look more or less like the following (call it graph 1):
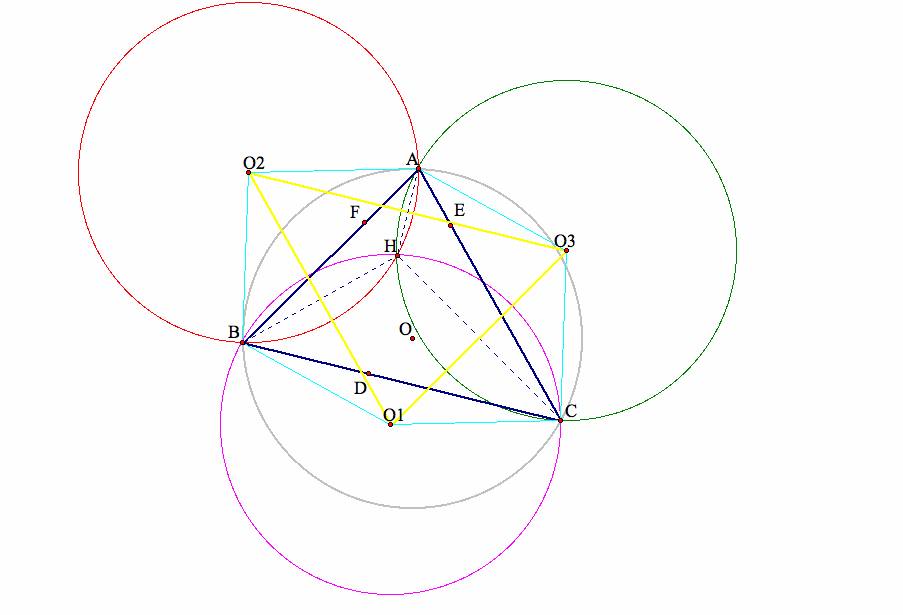
The next step is to see what happens if any vertex of the triangle ABC was moved to where the orthocenter H is located?
If we move the vertex A of triangle ABC to where the orthocenter H is located,
then the grey circumcircle of triangle ABC and the pink circumcircle of triangle HBC will overlap.
The following graph (graph 2) demonstrates the case when we move vertex A to H:
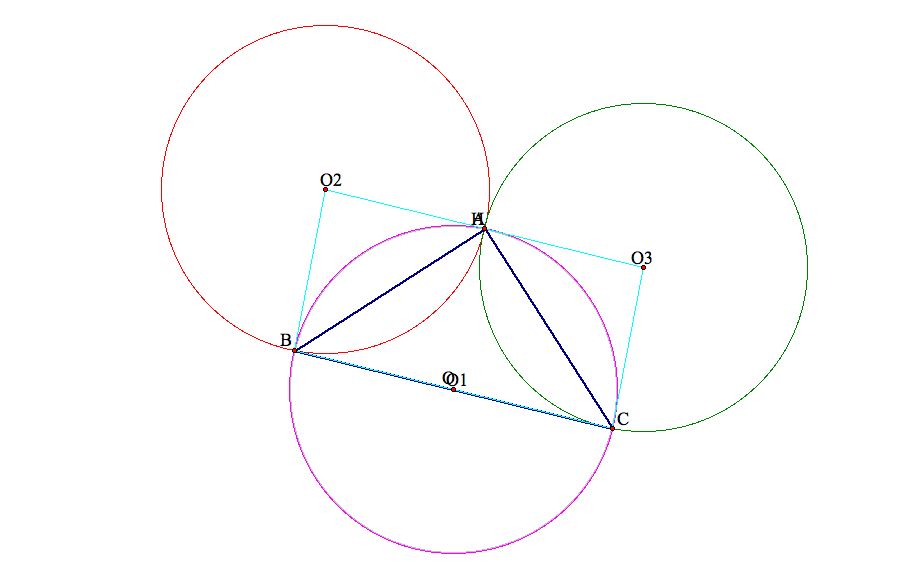
If we move vertex B of triangle ABC to where the orthocenter H is located,
then the grey circumcircle of triangle ABC and the green circumcircle of triangle HAC will overlap.
The following graph (graph 3) illustrates this case:
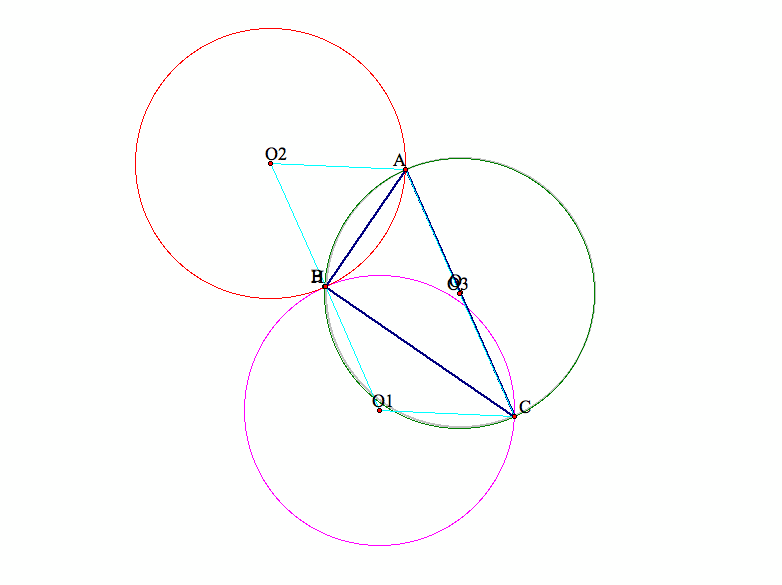
Finally, if we move vertex C of triangle ABC to where the orthocenter H is located,
then the grey circumcircle of triangle ABC and the red circumcircle of triangle HAB will overlap.
The following graph (graph 4) illustrates this case: