

Assignment IX: Pedal Triangle
by
Rui Kang
In this investigation, we introduce what a pedal triangle is, the location of a pedal triangle in relation to a given triangle,
and several special cases where the pedal point happens to be the centroid, the incenter, the orthocenter... of a given triangle.
Let's recall the definition of a pedal triangle:
Given a triangle ABC and any point P in the plane,
the triangle formed by the perpendiculars to the sides of ABC is called the pedal triangle for the pedal point P.
First, let's observe a case where the pedal triangle lies outside of the original triangle:
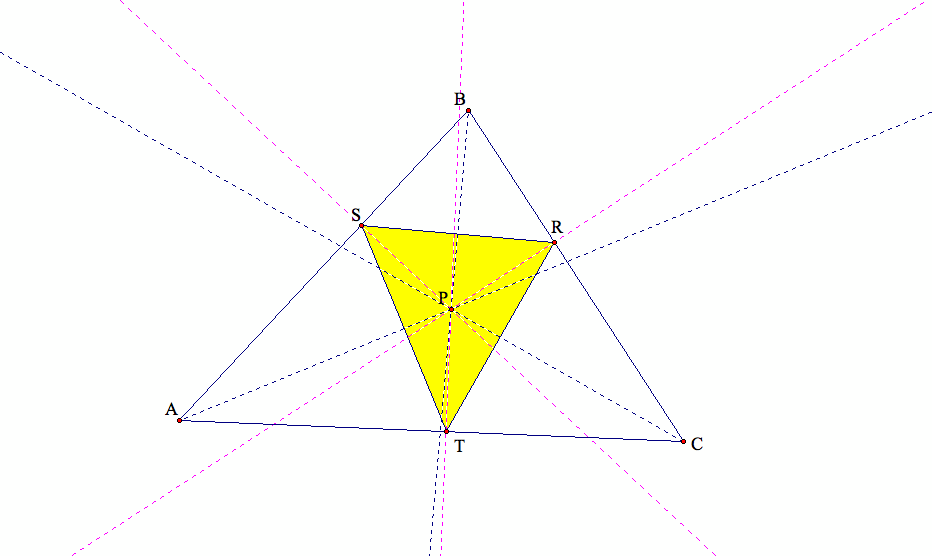
Next, let's observe a case where the pedal triangle lies inside of the original triangle:
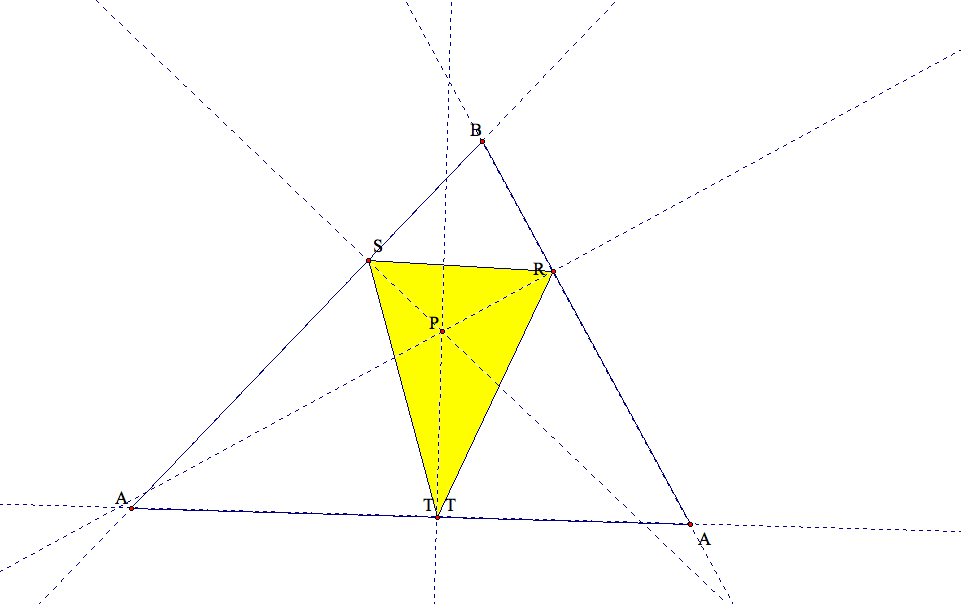
From the above two cases, we know that it is possible for a pedal triangle to be either outside or inside a given triangle.
The following series of graphs demonstrate what happens when the pedal point is located at some very special points with respect to a triangle.
(1) What if pedal point P is the centroid of triangle ABC?
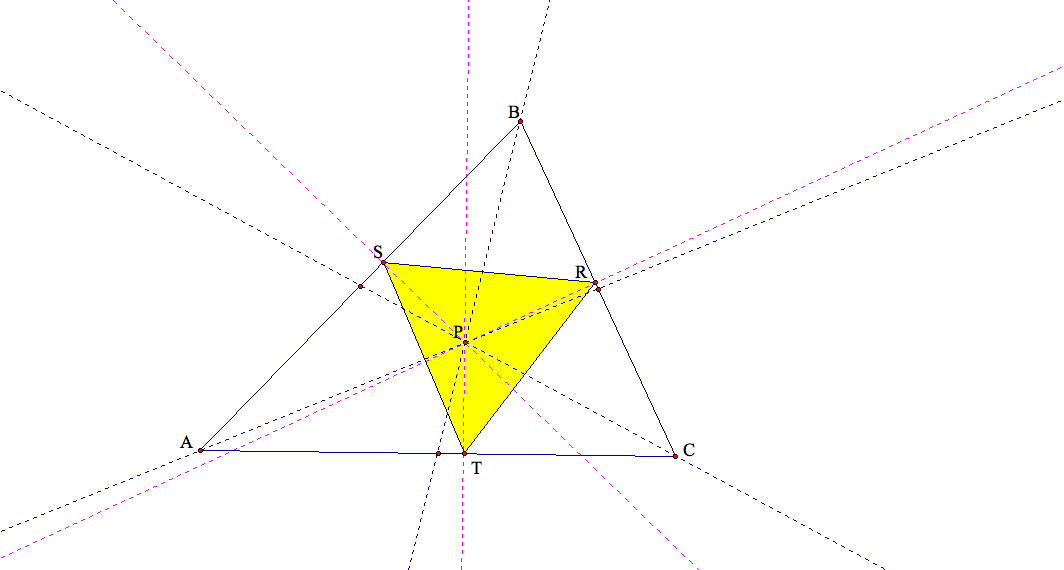
We observe that if P is the centroid, then our pedal triangle is always located inside triangle ABC.
Our pedal triangle will never move outside of our triangle ABC.
(2) What if pedal point P is the incenter of triangle ABC?

The conclusion here is pretty much the same as if P is the centroid of triangle ABC.
In particular, we observe that if P is the incenter, then our pedal triangle is always located inside triangle ABC.
Our pedal triangle in this case will never move outside of triangle ABC.
(3) What if pedal point P is the orthocenter of triangle ABC?
What if othocenter is inside triangle ABC? What if othocenter is outside of triangle ABC?
We know that if the pedal point P is the orthocenter of triangle ABC,
then by definition, our pedal triangle is also the orthic triangle of the given triangle ABC.
The location of the pedal triangle, however, changes depending on where the orthocenter (also our pedal) is at.
If the orthocenter is inside triangle ABC, then the orthic triangle, i.e., our pedal triangle is also located inside triangle ABC:
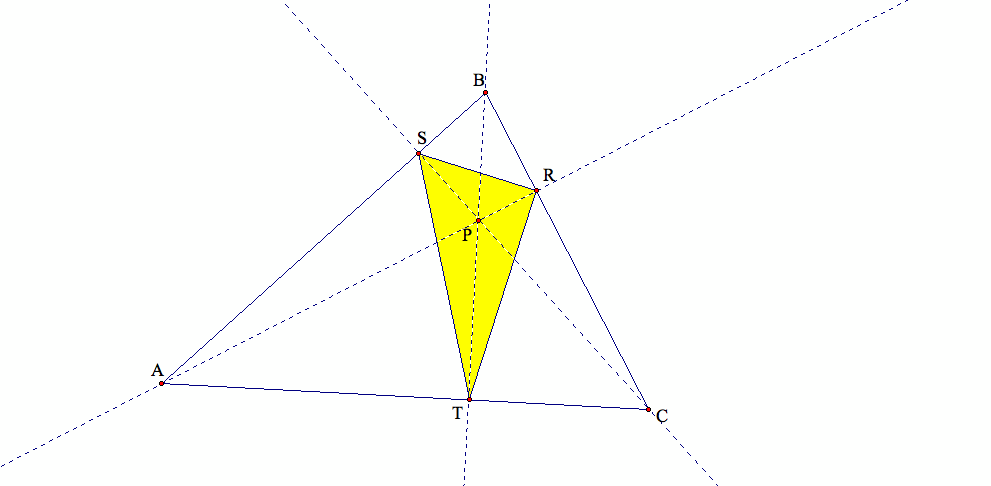
If the orthocenter is outside of triangle ABC, then part of the orthic triangle, i.e., part of our pedal triangle also lies outside of triangle ABC:
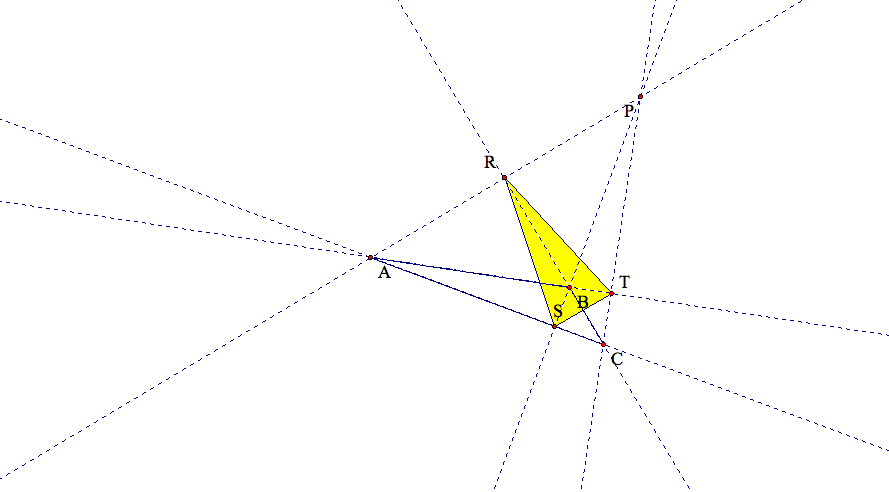
(4) What if the pedal point P is the circumcenter for triangle ABC?
We know that if the pedal point P is the circumcenter for triangle ABC,
then by definition, our pedal triangle is also the medial triangle of the given triangle ABC.
The location of our pedal triangle is always inside triangle ABC even if the circumcenter is outside of triangle ABC.
In the first graph below, we show the case when the circumcenter is inside triangle ABC.
In the second graph below, we show the case when the circumcenter is outside of triangle ABC.
Note that in both cases, our pedal triangle is located inside triangle ABC.
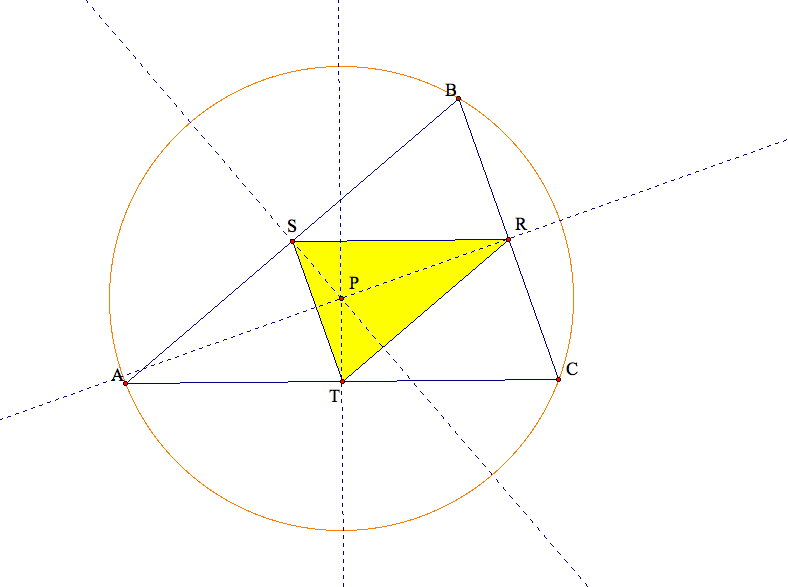
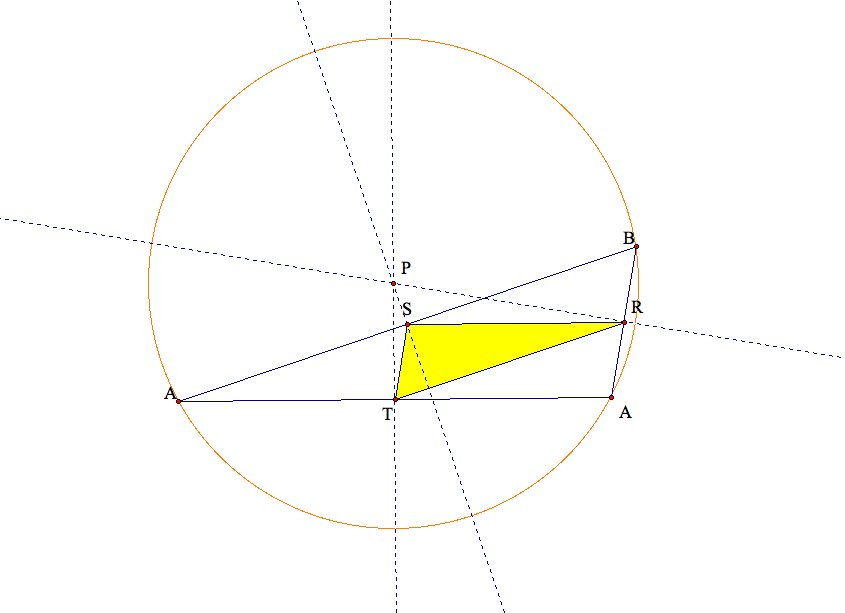
(5) What if pedal point P is the center of the nine point circle for triangle ABC? Even if outside ABC?
Recall what a nine-circle is? It is the circle that passes through the following nine points:
the three midpoints of each side of the triangle, the three foots of each altitude, and the three midpoints of the segment connected by each vertex and the orthocenter.
The center of a nine-point circle is located at the circumcenter of the medial triangle, i.e., the intersection of the three perpendicular bisectors of the medial triangle.
Now go back to our original question: where the pedal triangle is located when the pedal point is the center of the nine point circle?
It seems that if the pedal point is inside triangle ABC, i.e., the center of the nine point circle is inside triangle ABC,
our pedal triangle also lies inside triangle ABC.
And when the center of the nine point circle, i.e., our pedal point lies outside of triangle ABC,
we find that part of our pedal triangle also lies outside of triangle ABC.
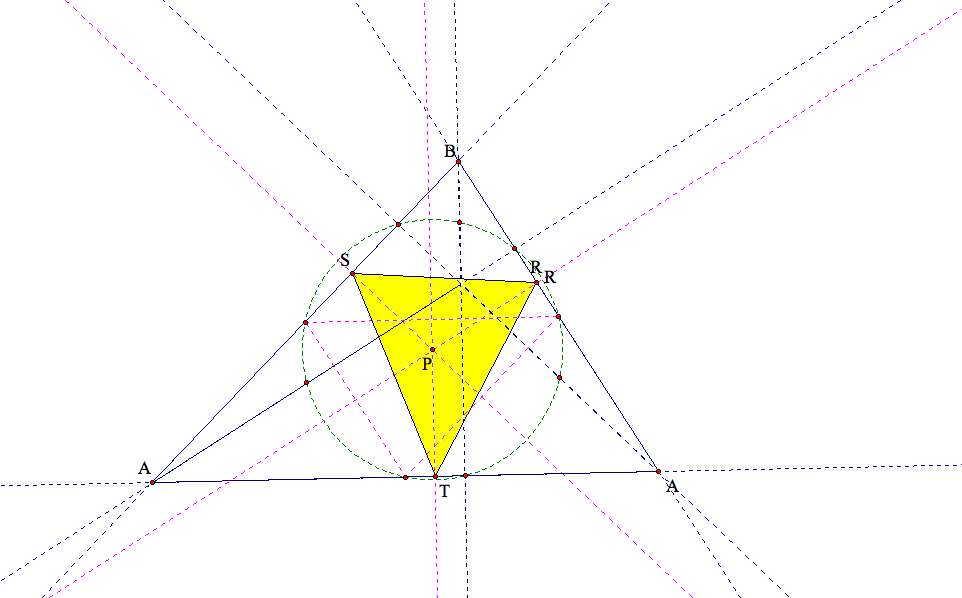
We may also observe a special case here:
When triangle ABC is an equilateral triangle, then its circumcenter C, the orthocenter H, and the center of the nine point circle are concurrent.
If the pedal point is then this concurrent point, our pedal triangle lies on the nine point circle.
In fact, the foots of the three altitudes are also the midpoints of the three sides of triangle ABC.
Therefore, the nine point circle becomes "six point circle" in this case. Here is an example:
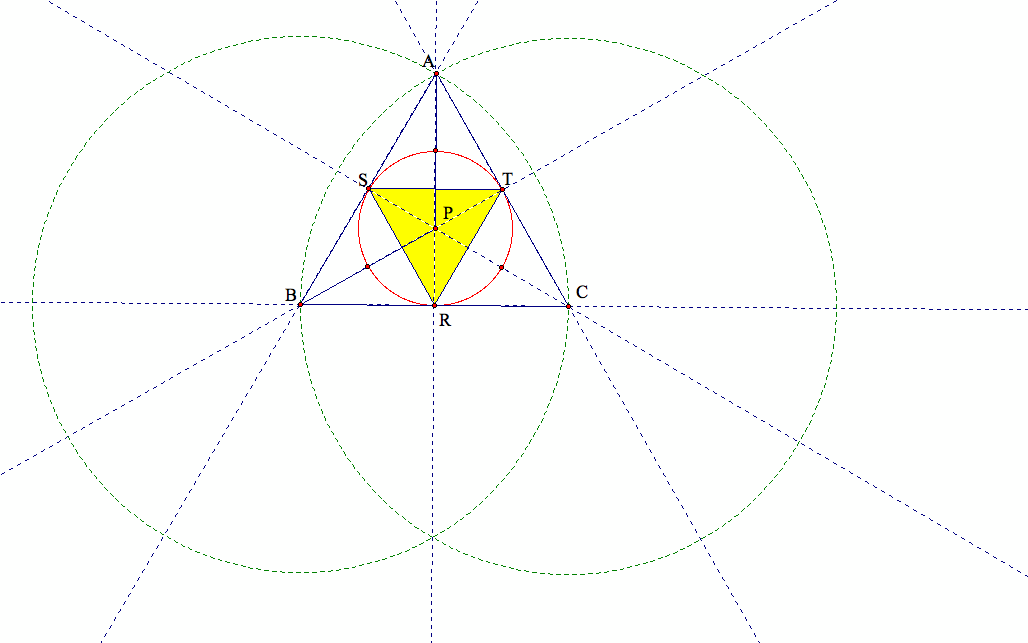
(6) What if pedal point P is on a side of triangle ABC?
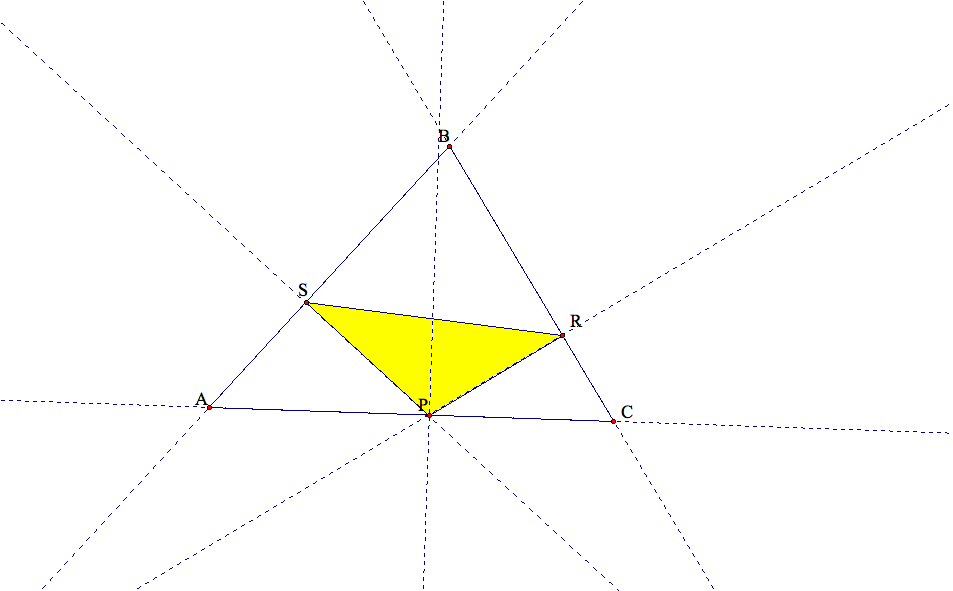
We observe that our pedal triangle is always inside triangle ABC and never moves outside.
In addition, our pedal point now becomes one of the vertices of the pedal triangle.
(7) What if pedal point P is one of the vertices of triangle ABC?
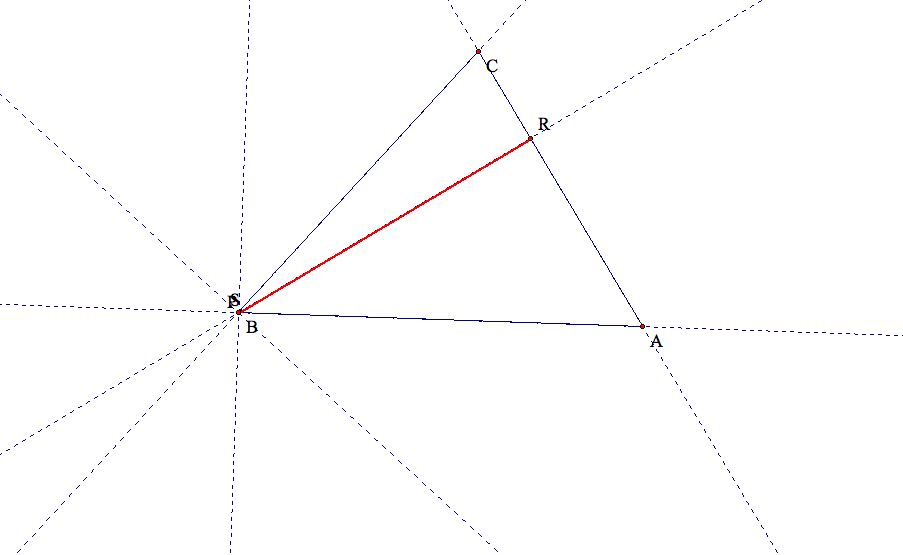
We see that if the pedal point P is one of the vertices of triangle ABC, then the pedal triangle will collapse into a line.
(8) And finally, we want to find all conditions in which the three vertices of the pedal triangle are colinear
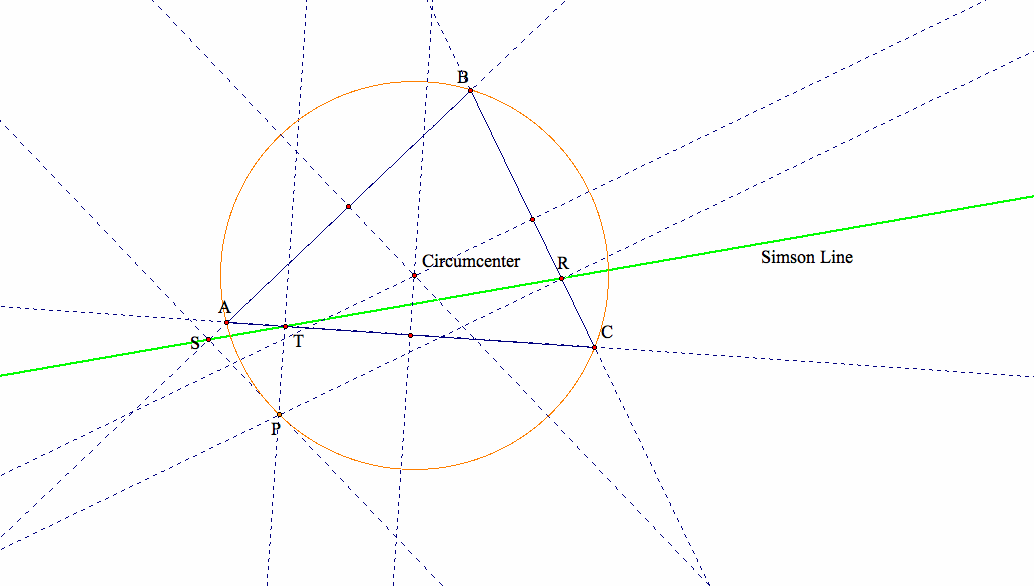
(that is, it is a degenerate triangle). This line is called the Simson Line.
We find that case (7) is just a special case when the pedal triangle collapses into a line or degenerate triangle.
In fact, whenever the pedal point P lies on the circumcricle of triangle ABC including when the pedal point P is any of the vertices of triangle ABC,
our pedal triangle collapses into a line, called the Simson Line.
Here is an example:
Finally, look at the following picture which illustrates the envelope of the Simson Line when we trace the pedal point as it moves along the circumcircle:

The above picture was retrieved July 12, 2009 from:
http://jwilson.coe.uga.edu/emt668/Asmt9/EMT668.Assign9.html