Brenda King
Exploring Quadratic
Transformations
Introduction
and generalization:
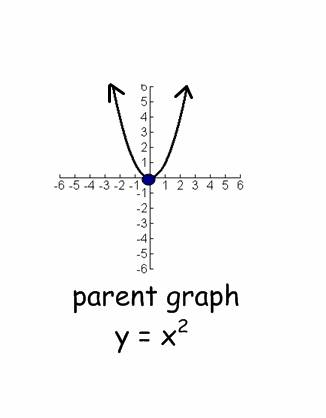
The basic
quadratic equation has the form y = ax2 + bx + c. When a = 1, b=0, and c=0, then the equation
is referred to as a parent graph.
Changing the values
of a, b, and c will cause either transformations or alterations to the graph shape.
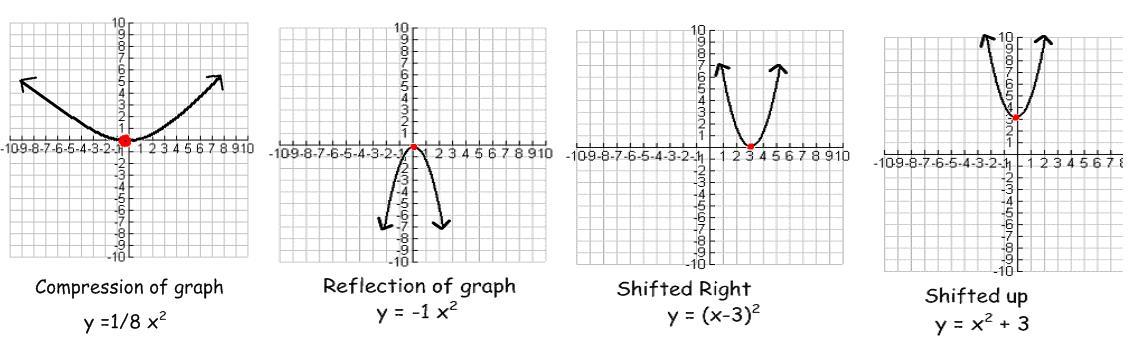
There are several
types of changes which can occur to the parent graph:
- The shape can be stretched or
compressed (made wide or narrow).
- The graph can be reflected across an
axis, such as the x or y – axis.
- The graph can be shifted left
or right, a horizontal movement.
- The graph can be shifted up or down,
a vertical movement.
- The graph can have a combination of
all of these changes.
Exploration:
The following
diagrams show some of the changes that can be made with various values
of a, b, or c.
Graph 1
Graph 2
Graph 3
Observations:
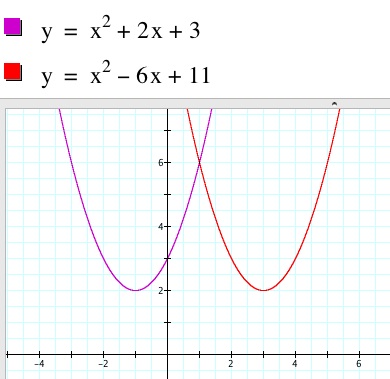
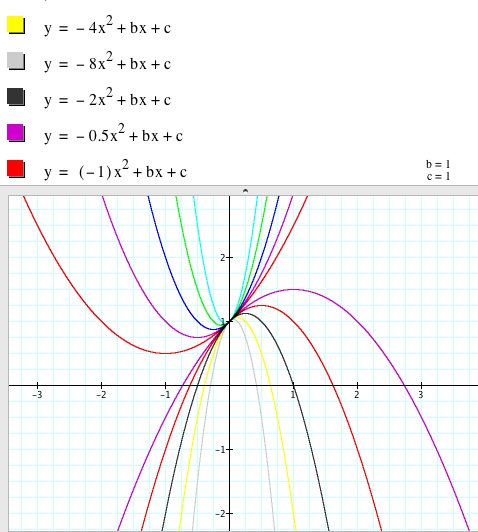
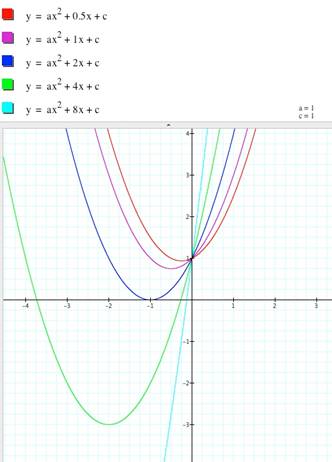
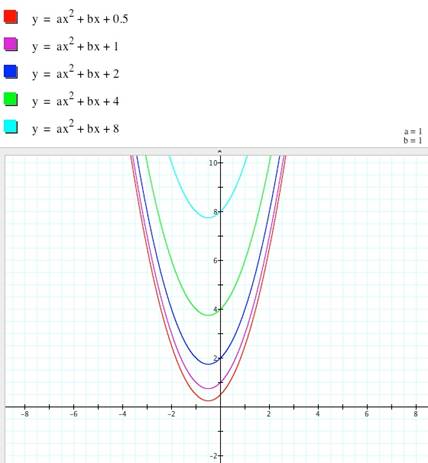
When changes are
made only to a and b, the y-intercept is shared by all the transformations
(remember no change in parameter c is being made).
The vertex changes
in all the graphs. See 1 and 2. When c is the only
value changed, then no common point is seen, see graph 3.
Reflection: The parabola will open upward when unknown a is
positive and downward when unknown a is negative.
Stretch/compress: For larger and larger values of a, the parabola
stretches (gets more narrow). For
smaller and smaller values of a, the parabola compresses, or becomes more flat.
Vertical shifts: For larger values of c, the graph moves
higher and higher in the vertical direction.
For negative values of c, the graph moves down lower and lower.
Specific
Example
Using one specific
example will help to demonstrate all of these changes.
Standard form: y = x2 + 2x + 3
Vertex form y = (x + 1)2 + 2
There are two ways
to write a quadratic formula 1) standard form and 2) vertex form.
There is an
advantage when graphing to use the vertex form of the quadratic. In this example, both forms will be used.
i. Overlay a new
graph replacing each x by (x - 4).
Standard
form: Y =
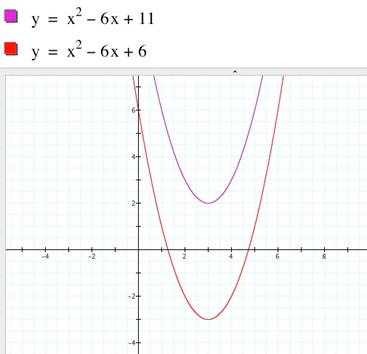
(x-4)2 + 2(x-4) + 3 = x2 - 6x + 11
Vertex
form: y = (x -3)2
+ 2
ii. Change the
equation to move the vertex of the graph into the fourth quadrant.
By subtracting a value, such as 5, the
graph will shift down enough to be in the fourth quadrant
Standard
form: y = x2
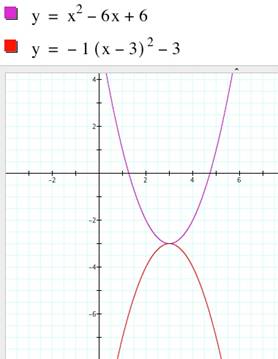
- 6x + 11 – 5 = Y = x2 - 6x + 6
Vertex
form: y = (x -3)2
+ 2 - 5 = (x -3)2 - 3
iii. Change the
equation to produce a graph concave down with the same vertex.
By replacing unknown a with a negative, the
graph will be reflected and face downward.
Standard
from: y = -1
x2 + 6x - 6
Vertex
form: y = -1
(x -3)2 - 3
i. Replacing with (x-4) ii. Moving vertically down to 4th
quadrant iii.
Reflecting with same vertex