Brenda King
Exploring Centers of Triangles
and the Nine-Point circle
Introduction:
Where three or more lines (or segments) intersect in the same point, the intersection is called a point of concurrency. If the three lines (or segments) are constructed from the sides or vertices of a triangle, then the point of concurrency is often referred to as a center for the triangle. In many cases the point does not appear to be in the center area and, in fact, may be located outside the triangle. Often, to distinguish the many different triangle centers which are possible, unique names are assigned to a triangle center. By naming centers the construction and properties associated with the center can be determined and recognized.
This investigation will
discuss three centers and a special circle associated with all three centers. The triangle
centers to be discussed are the centroid, orthocenter, and circumcenter.
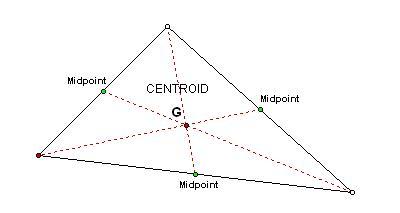
CENTROID
A centroid is the center of Gravity of a triangle.
It is often labeled with a G (for gravity) for this reason. The centroid is the common intersection of three medians. A median for a triangle is a segment that
goes from a vertex to the midpoint of the opposite side.
When exploring in geometry sketchpad, I found that
the centroid always stayed inside the triangle regardless of the triangle size
or shape.
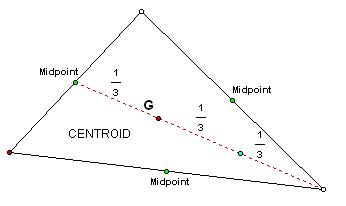
The centroid divides the median into lengths
with a ratio of 2:1. The longest length
is on the same side as the vertex used to create a particular median.
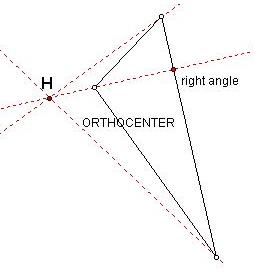
ORTHOCENTER
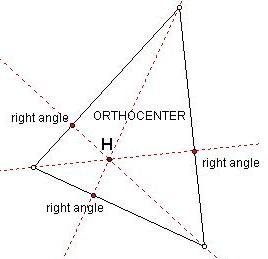
An Orthocenter of a triangle is the common
intersection of the three lines containing the altitudes. An altitude is a
perpendicular segment from a vertex to the opposite side. The orthocenter is traditionally labeled H (which
is helpful since the letter H itself contains right angles and provides a hint to the construction). The word ortho means right.
When exploring an orthocenter in geometry sketchpad,
I found that the orthocenter can be located inside, outside or on the triangle
(in the case of right triangles). For
acute triangles, the orthocenter is inside the triangle. For obtuse triangles, the orthocenter is
outside the triangle and “exits” the triangle through a vertex.
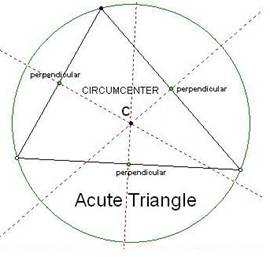
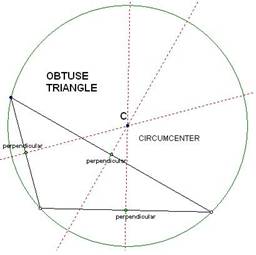
CIRCUMCENTER
A circumcenter of a triangle is a point in the plane
equidistant from the three vertices of the triangle. This center is traditionally
labeled C. The circumcenter is on the
perpendicular bisector of each side of the triangle.
When exploring a circumcenter in geometry sketchpad,
I found that the circumcenter can be located inside (acute triangle), outside
(obtuse triangle) or on the triangle (right triangles). For obtuse triangles, the circumcenter
“exits” the triangle through a midpoint.
Another interesting fact about the circumcenter is that
it is the center of a circumscribed circle around the triangle.
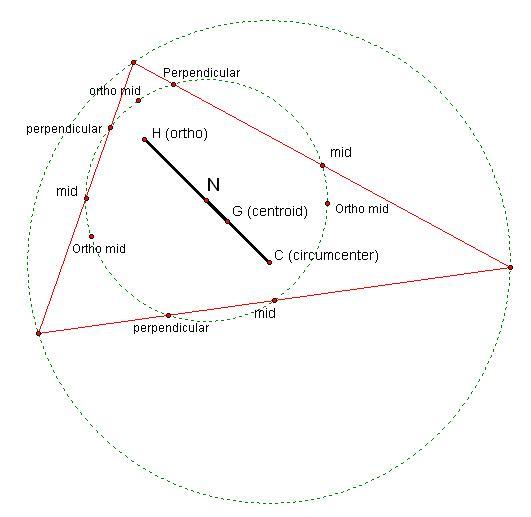
Nine-Point circle
A discussion of these centers would not
be complete with out bringing them all together into a special circle called
the Nine-Point circle as shown below with the nine points labeled. The Nine-Point circle for any triangle passes
through the three mid-points of the sides (labeled mid), the three feet of the
altitudes (labeled perpendicular), and the three mid-points of the segments from the
orthocenter vertices (labeled ortho mid).
All three of these centers are collinear
(lie on the same line). The line passing through the points is
called the Euler line. The center of the
circle, N, also has some neat properties.
It is in the middle of the orthocenter and circumcenter. If the circumcircle is dilated with respect
to the orthocenter by ˝, then the result is the Nine-Point circle.