
Brenda King
Using Geometer’s Sketchpad
to solve problems
Introduction:
Solutions to problems have
become easier to find with the use of technology. High school students expect solutions to be integers or easy to find. The real world
does not work this way. What is
true, however, is that in order to maintain student interest in a problem, the
dirty business of getting a numerical solution needs to be minimized. By using technology, the “messy”
solutions can be found without lengthy calculations or become frustrating for students.
To quote G. Polya “You do
not take up a problem, unless it has some interest, you settle down to work
seriously if the problem seems instructive, you throw in your whole personality
if there is a great promise” (How to
Solve it, page 65). These are the kinds of problems we want to give students to work.
Teachers are always looking
for the instructive problems to give students which also provide interest. By using technology, such as Geometer’s
Sketchpad, students can immediately get involved in the problem, see the
instructive side of the problem, and, as a bonus, get an exact solution to the
problem without tedious calculations.
The
Problem:
An example of a problem that
makes good use of technology is the following:
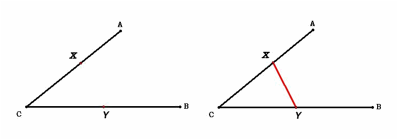
Given three points A, B, and
C. Draw a line intersecting AC in
the point X and BC in the point Y such that AX = XY = YB
What makes Geometer’s Sketchpad valuable in any
problem is the flexibility in drawing the given information and the dynamic
placement of the unknowns.
The point x can be placed
anywhere on the segment CA and is not yet fixed. The placement of y depends on the placement of x.
The locus of all points equal distant to point x can
be found by constructing a circle centered at x with a desired radius. In this
problem, the radius needs to be of length AX. Diagram 1 shows that AX=XY
because y and A are both on circle A.
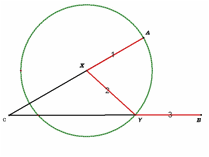
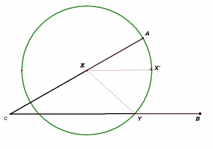
Diagram 1 Diagram
2
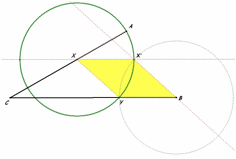
The task to this problem is to make three segments AX , XY, and YB equal to each other.
In order for YB to equal AX and XY, certain
adjustments will need to be made to the placement of point x. The dynamic nature of sketchpad makes
this easy to do.
If a radius, XX’, is drawn parallel to segment CB through X, shown in diagram 2, then the correct placement of x will form a rhombus using point B.
By definition, the sides of a rhombus are equal to each other. See Diagram 3 (or open the attached sketchpad for a better view).
Diagram
3 Diagram 4
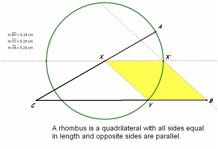
By constructing a second circle with radius AX
centered at point B, the solution to the problem is to move point x until circle
B intersects point Y. The
measurements of the segments will verify equal measures. See Diagram 4.
The solution for the particular diagram drawn is to
have the three segment length = 5.23.
An angle will also need to be determined for the placement of x.
The solution is not an integer, as hoped by
students, but relatively painless when working with technology.
Here is a sketchpad file with these results.