Brenda King

Retrospective summary of

Tangent Circles

Introduction:

This investigation had to do with the following problem:

Given two circles and a point on one of the circles, construct a circle tangent to the two circles with one point of tangency being the designated point. 

For the purpose of this write up, I distinguish between the two given circles as large and small.  The constructed tangent circle will be colored red in all diagrams and the given circles will be colored black.  The green line segments will be used to determine relationships that were discovered from the trace and locus of points in the investigation.

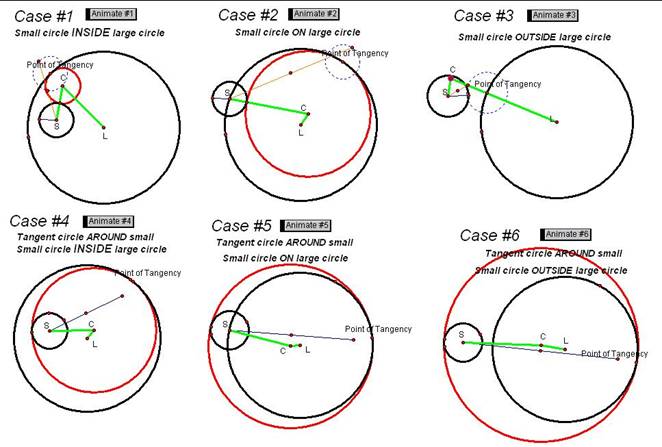
While doing this investigation, I explored six cases of tangent circles.  The cases depended on two things 1) the placement of the given circles (inside, intersecting or outside each other) and 2) the construction of the tangent circle either around or exterior to the smaller circle.   The following diagram shows the six cases considered.

Trace and locus resulting in an ELLIPSE

An ellipse is the set of all points, C(x,y), the sum of whose distances from two distinct points (foci), S(x,y) and L(x,y) is constant.

The following 3 traces and locus arrangements resulted in an ellipse. The trace of the midpoint was a circle.

           

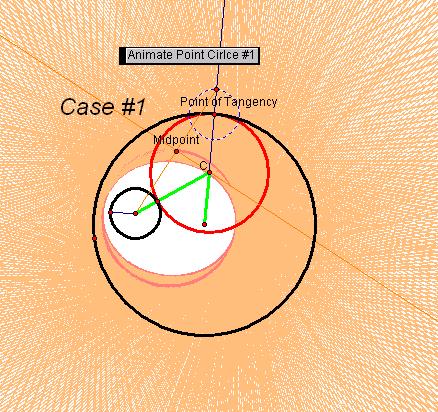
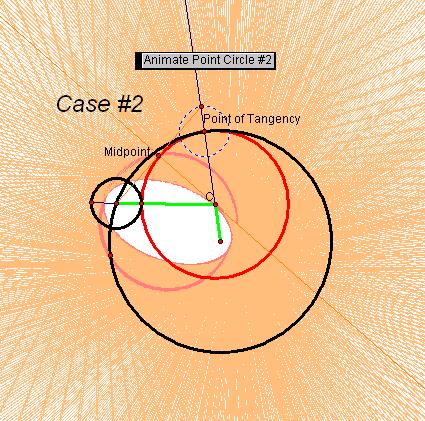
The diagram below identifies key components for discussion.

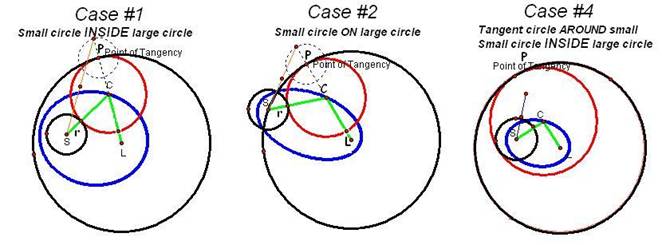
Center of small circle, S.            Radius small circle, r.                                   

Center of large circle, L.            Radius of large circle, R = segment PL           

Center of tangent circle, C.        Radius of tangent circle, RT , segment PC                 

 

See green segments for the following discussion.

For Case #1 and #2

Length of CL = PL – PC = R - PC

Length of CS = PC + r

Sum of CL + CS = R – PC + PC + r = R + r = Radius large + Radius small = constant

 

 

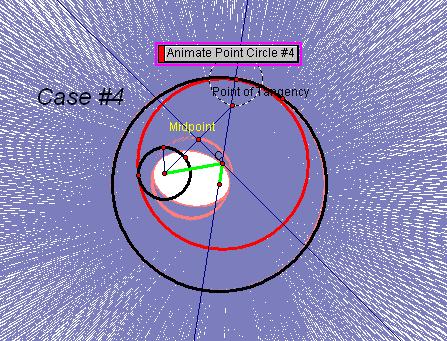
For case #4, where tangent circle is outside small given circle,

 

Length of CS = R - PC

Length of CL = PC – r

Sum of CS + CL = R – PC + PC - r = R - r = = Radius large - Radius small = constant

 

Trace and locus resulting in a Hyperbola

A hyperbola is the set of all points C(x,y) the difference of whose distances from two distinct fixed points (foci) is a positive constant.

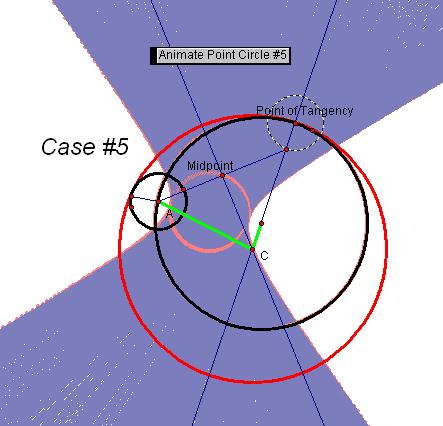
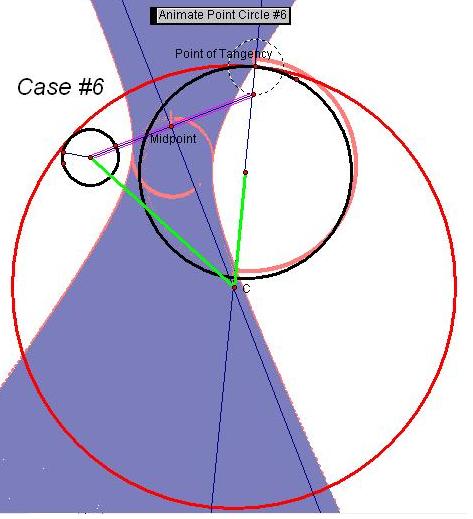
The case #3, 5, and 6 resulted in a hyperbola.  The midpoint again was a circle in all cases.

        

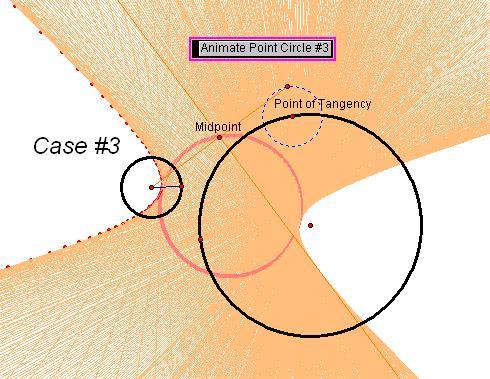
The locus of points alone are shown below:

               

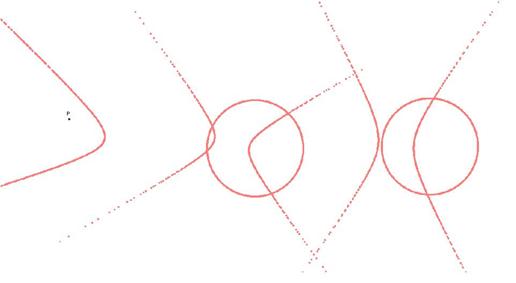
I found it interesting that in case 3, the locus of points displayed a parabola where the trace of the tangent line showed a hyperbola.  This result must be from a limiting situation special to case 3.

 

Case #5 and #6 are disjoint circles (small circle completely outside large circle).  Both resulted in a hyperbola trace and locus. 

Interestingly, where the two given circles intersect each other, case #2 and #5, the results were different from each other.  For case #2, an ellipse pattern was found and in case #5 a hyperbola was found.  If I did further explorations, I might be able to discover why Case #4 resulted in an ellipse, even thought the construction of the tangent circle was like both case #5 and #6.

Summary chart

 Here is a sketchpad file with all the results pulled together.

RETURN