
Brenda King
Pedal Triangles
Introduction:
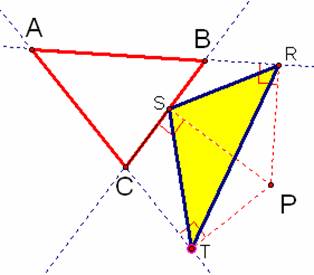
Pedal triangles are
constructed by starting with any triangle, ABC and a 4th point
located anywhere in the plane. The vertices
to pedal triangle, RST, are formed from the intersection of perpendiculars to
the sides of triangle ABC (extend sides if necessary) where the perpendiculars also
pass through the point P. See diagram 1.
Diagram 1.
This investigation will
explore what happens when the point P is relocated to coincide with the Circumcenter
of triangle ABC.
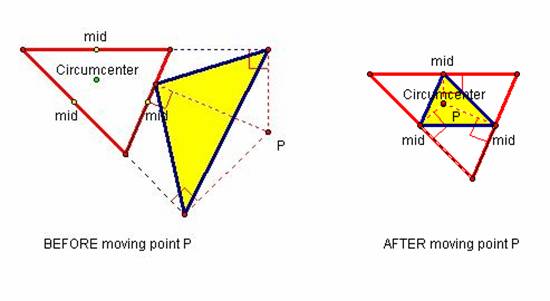
Point P used as circumcircle for ∆ABC
The circumcenter of a triangle is the point in the
plane equidistant from the three vertices of a triangle. Since all points equidistant from two points
lie on the perpendicular bisector of the segment determined by the two points,
the circumcenter is located on the perpendiculars bisector of each side of the
triangle.
From the way the Pedal triangle was constructed,
with perpendiculars at the vertices of the triangles, moving the point P to the
circumcenter also moves the perpendiculars to the midpoints. The Pedal triangle, RST, has turned into a
medial triangle!
Diagram 2
The
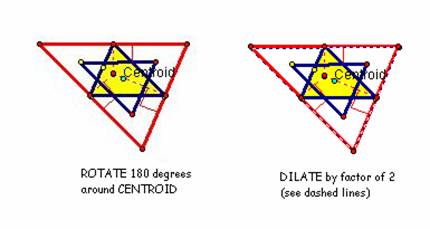
medial triangle has unique characteristics of its own. The medial triangle can be viewed as similar
to the image of ∆ABC. To explore this idea, I rotated ∆RST 180° around
the centroid of ∆RST. The Centroid of a triangle is the common
intersection of the three medians. Next I
dilated ∆RST by a factor of 2. See diagram 3
Diagram 3
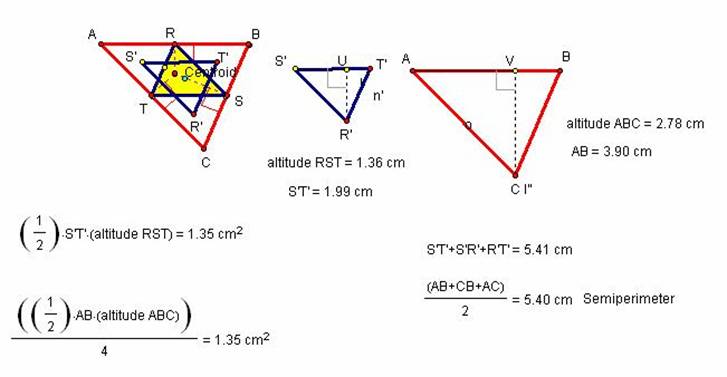
It also follows from this that the perimeter of the
medial triangle equals the semiperimeter of triangle ABC, and that the area is
one quarter of the area of triangle ABC.
I checked out these properties in Geometry Sketchpad as shown in Diagram
4
Diagram 4
To see sketchpad file click here.