Sinusoidal Modeling
by Brenda King
Introduction:
The term sinusoid was first use by Scotsman Stuart Kenny in 1789 while observing the growth and harvest of soybeans. It is the application of sinusoidal modeling that makes its use in the secondary school environment so valuable. When teaching students the value of sinusoidal models and graphs, such as sine and cosine functions, students often feel like they must memorize formulas and apply them with little recollection or understanding. The purpose of this write up is to use technology, websites, and guided discovery to assist students in understanding basic sinusoidal graphs and applications. In this way, students can discover for themselves the key concepts and how to apply them without asking the questions “When am I ever going to use this?”
A periodic function is one that repeats itself over time. One way of creating a periodic function is by moving a point around a circle and defining functions from the corresponding characteristics.
The Geomery Sketch pad file Sine and Cosine functions will assist students learning how Sine and Cosine functions can be created.
With the cyclical nature of the real-world there are many opportunities for periodic functions to be used as mathematical models. To begin this discussion we need to recall a few important ideas for sinusoidal functions such as the effect of the parameters within a basic equation of the form y=a sin(bx-c)+d. Each parameter can be identified as a: Amplitude, b: Period or the length of one full cycle, c: Phase Shift or horizontal movement of the graph and d: the vertical Translation.
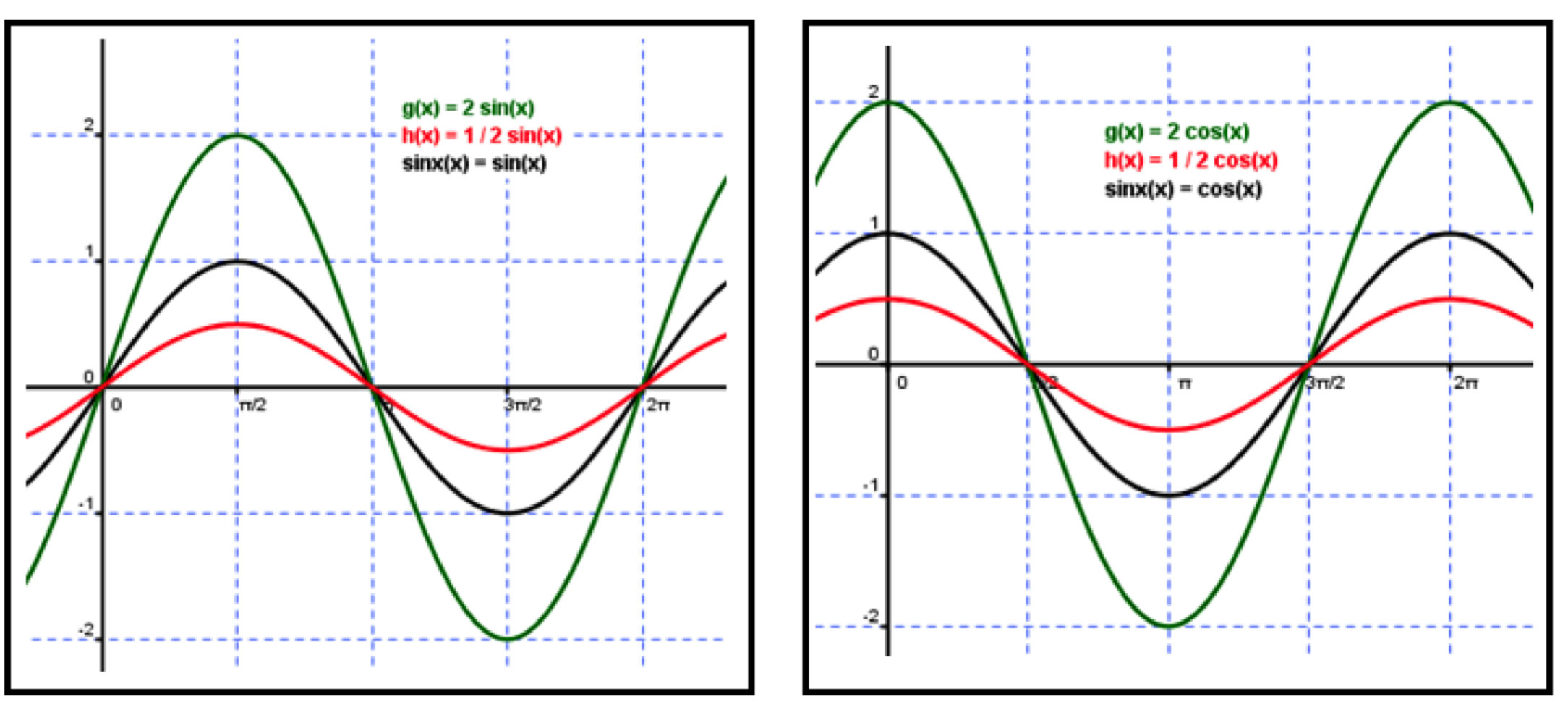
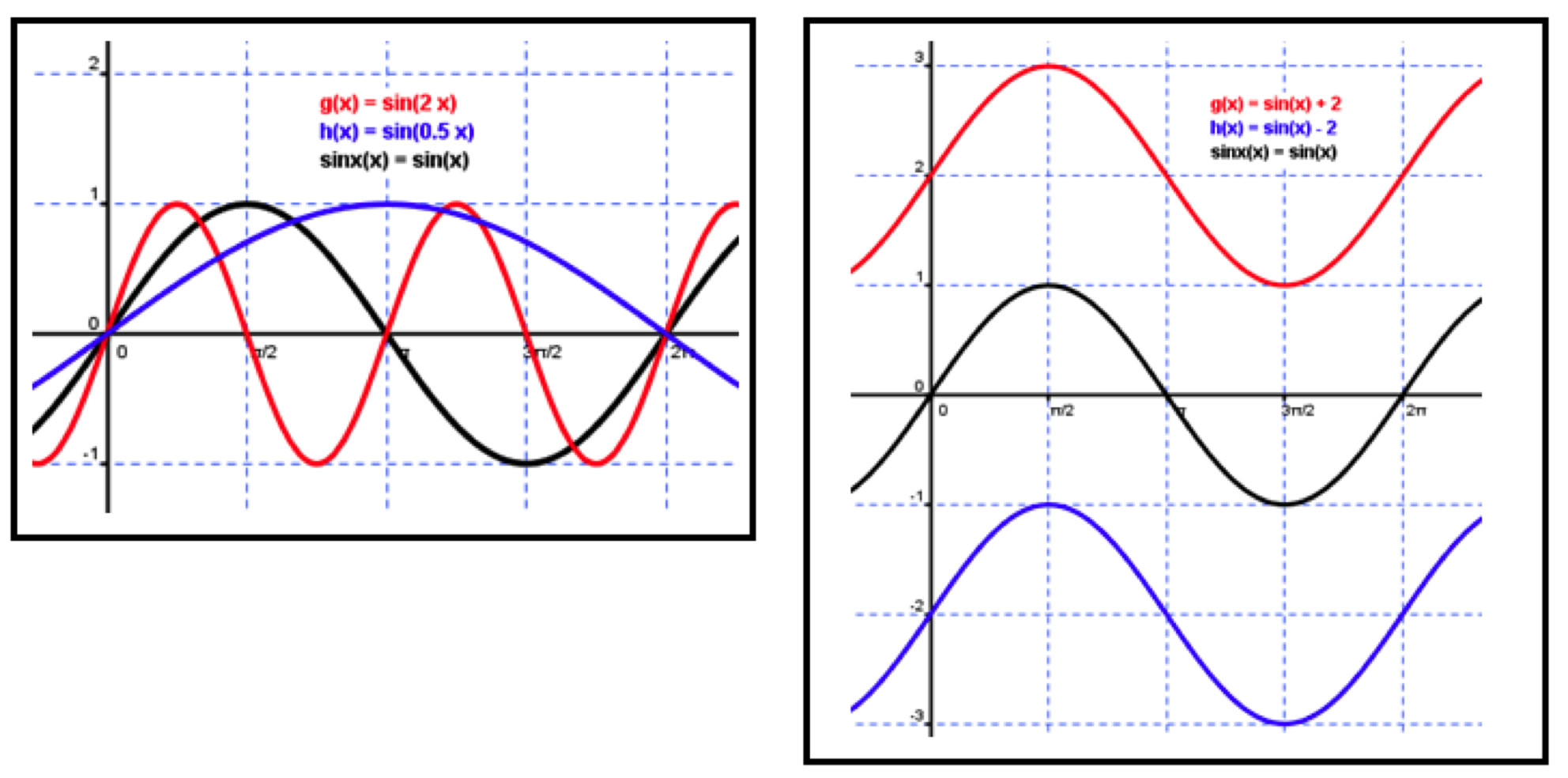
Using a free software, Geogebra, students can investigate the effect of changing each parameter in y=a sin(bx-c)+d by using SLIDERS in the file Exploring transformation.
I had never used this program before creating the files for this write up and found it to be very easy to use and adjust.
The link to download Geogebra for classroom can be found here: Geogebra site.
Click on any of the following files for additional examples of each type of transformation or dilation to a sine function.
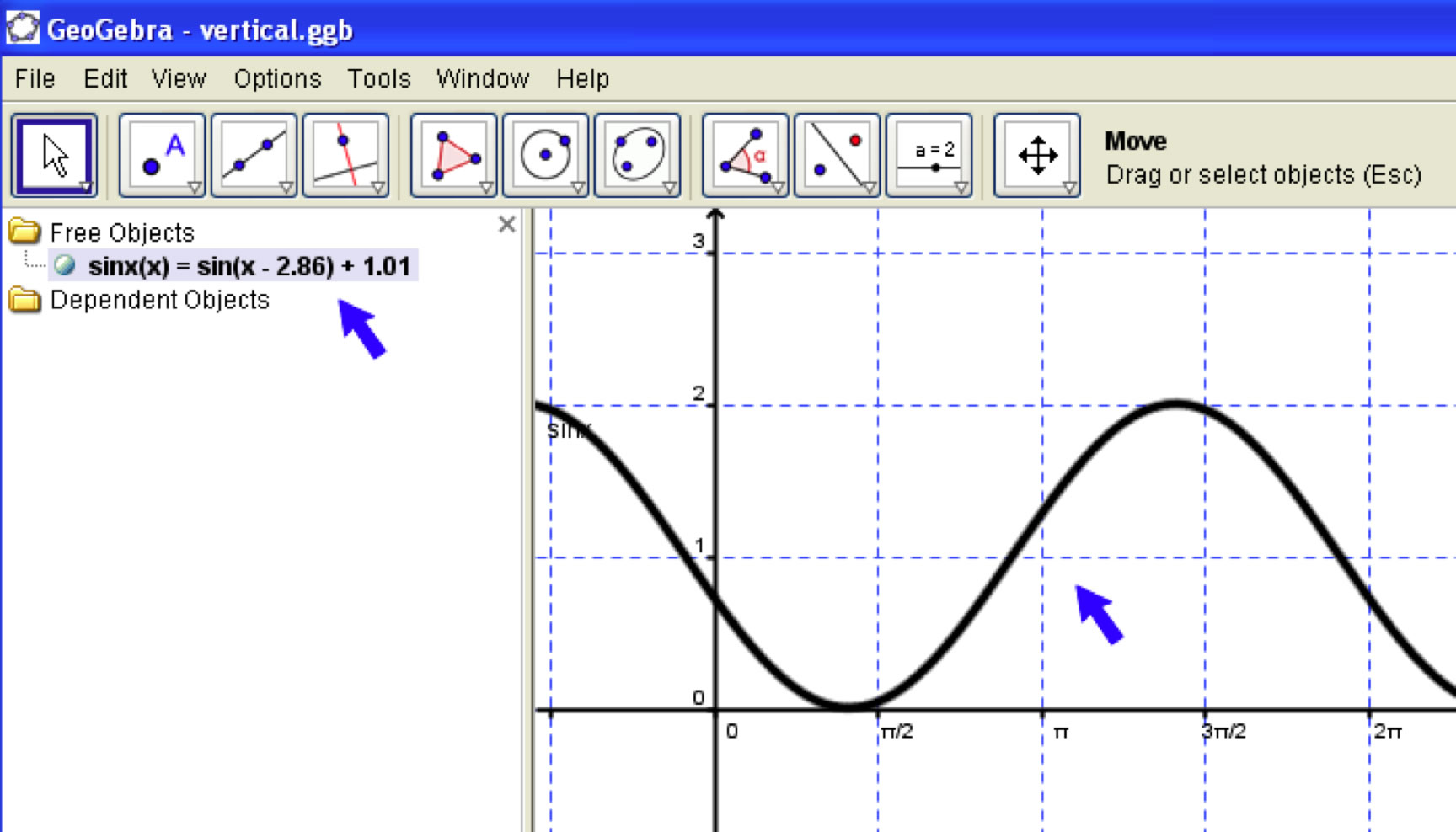
One of the really valuable features of the Geogebra program is the ability to move graphs around and see the corresponding changes in the equation itself.
The figure below shows an example of how this can be done. In addition, the attached file has already been created for students to use directly for the same observations.
The following website also provides demonstrations of many of the characteristics of trigonometric equations Website.
There are also some excellent calculators that can be used to graph periodic functions.
The following site can be of some value. Finding your way around the calculator
Application of Sinusoidal equations
A direct application of Sinusoidal Equations can be found by Average Monthly Temperatures. Students can select record temperatures from anywhere in the world by using the website http://www.weatherbase.com such as
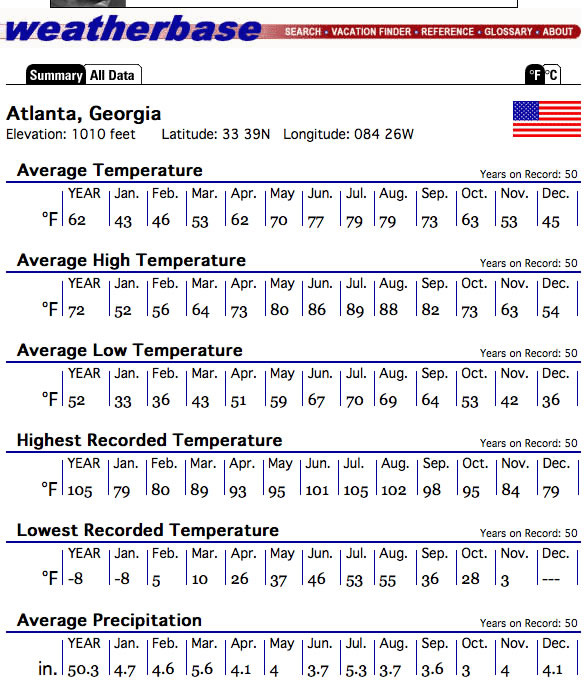
A sample project which can be done by students can be found here along with an EXCEL template file