Mathematics in Construction
Introduction:
In the real world of building construction there are many rich problems which can be used to build sense making and reasoning skills for students.
The website “PBS for Teachers” offers ready to use lessons based on NTCM standards as an example.
Some activities on this site include How many Shingles, Pricing a Deck, and Fencing the Yard.
The Pythagorean Theorem is used extensively in designing and building structures, especially roofs.
Gable roofs, for example, are made by placing two right triangles together. Specialized terms help to explain the triangle relationships in roof construction.
Terminology
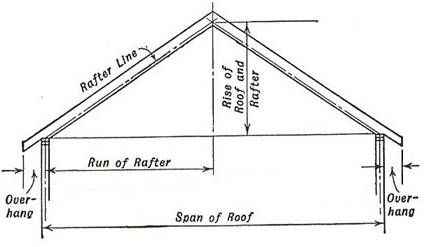
The span is the length from the outside wall to the outside wall of a building. Because construction is often made up of multiple layers of wood, building plans often provided detailed descriptions to make clear where to begin or end measurements.
The RUN is one-half the span. Units of run are typically based on 12 inches.
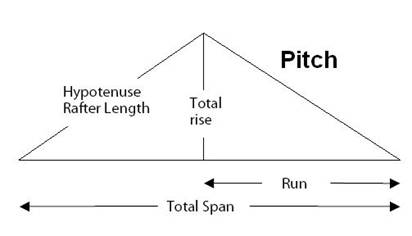
Carpenters do not refer to the angle of a roof as 300 or 600, but prefer to use the pitch of the roof.
The pitch is a ratio of vertical to horizontal measurements.
If a plan calls for a 6/12 pitch roof, then the architect wants the slope of the roof to go up six inches for every 12 inches of horizontal run. Carpenters prefer to use Pitch in calculations instead of rise and run.
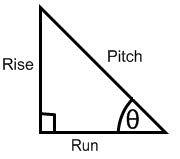
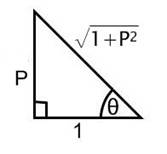
Key Formulas:
Length of rafter =
Suppose a roof has a rise of 18 inches and a run of 15 feet. How long is the rafter?
Length of rafter = 
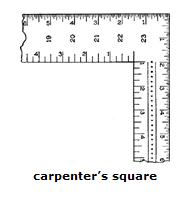
Only very simple tools are needed to cut r roof rafters such as a saw, framing square (or carpenters square) and a tape measure.
The framing square is made up of two legs joined at the heel to form a right angle. The longer leg of the framing square is called the body and the shorter one leg is called the tongue. To measure a 10/20 roof pitch, place the 10 on the tongue and the 20 on the body. When a piece of lumber is added to a carpenter’s square, it becomes a right triangle.
Math Application
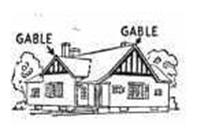
A Gable is a triangle formed by a sloping roof. A building may be front-gabled or side-gabled.
Consider structures where two roofs intersect as shown here.
When two roofs intersect, a valley rafter is formed.
The valley formed from the two common rafters and can be thought of as the diagonal in a rectangular solid.
From geometry we know that right
triangles are similar therefore the sides of one triangle is proportional to
the sides of the other. When the Pitch
of the two intersecting roofs are not the same, see Gable picture, then the
valley rafter calculation will involve a proportion.
Other formulas needed to work with Roofs are as follows:
Slope Factor =
Fnd the length of the valley rafter given the following measurements.
L1=8 feet,
L2=10 feet, Pitch 1 = 1, Pitch 2 = 0.8, 
Length of Valley rafter=
A Geometry Sketchpad showing intersecting roofs with different pitches is attached. Included in the sketch is the placement of the Rectangular Solid whose diagonal forms the roof valley. Click here.
The next diagram can be used to create a paper version of intersecting roofs and corresponding valley rafter.
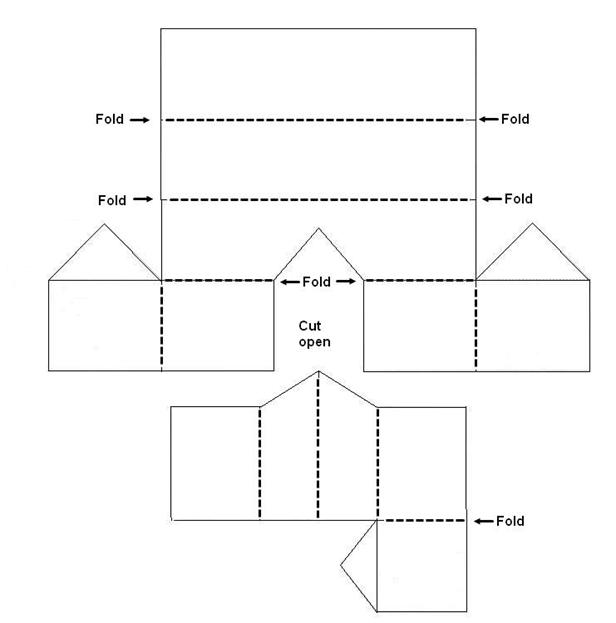
Reference: http://daveosborne.com/dave/articles/framing-square.php
http://faculty.matcmadison.edu/kmirus/
(Kevin Mirus,
Grazda, Jansson, and Minrath, Handbook of Applied Mathematics, D. Van Nostrand Company, Inc., 1966