Assignment 1:
Sine Function
by
Wenjing Li
#5. Examine graphs of
y = a sin(bx + c)
for different values of a, b, and c.
1. For a=1, b=1, c=0
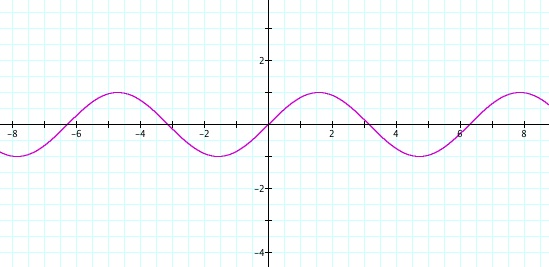
This is the standard sine function graph. The graph of sine function has max value 1, min value -1, period 
and the starting point of one period is 0.
We let a vary.
2. For a=-1, b=1, c=0
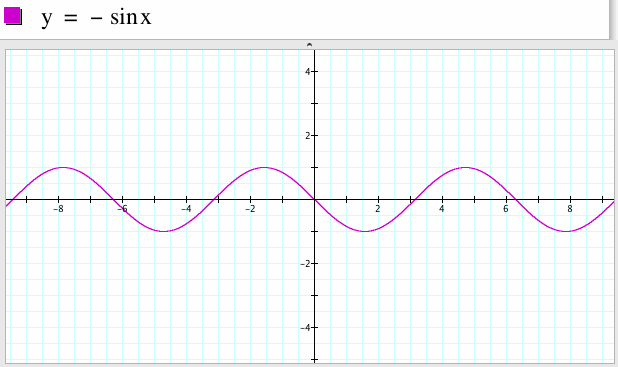
If we reflect the graph of y=sin x with respect to the x-axis, we get the graph of y=-sin x.
We let b have different values.
3. For a=3, b=1, c=0
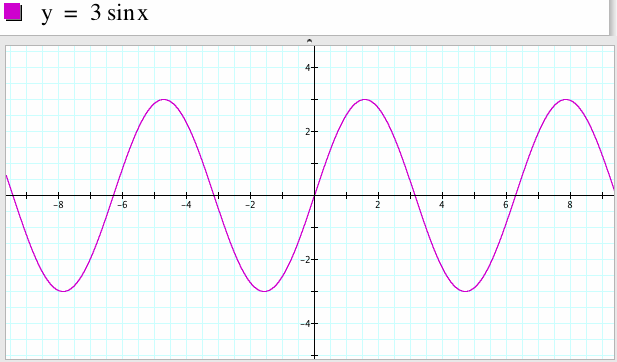
The shape of the graph of y=3sin x is similar with the graph of y=sin x, but the maximum value is 3 and minimum value is -3 which is the absolute value of a. To generalize this, the graph of y=a sin(bx+c) has maximal value |a| and minimal value -|a|.
4. For a=1, b=2, c=0
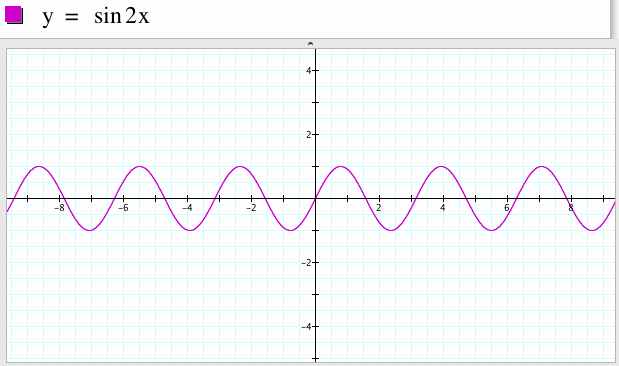
The period of the sine function y=sin x is , and the period of the function y=sin 2x is 
. In general, the period of the function y=sin ax is /|a|.
Now let examine what will happen if c have different values.
5. For a=1, b=1, c=1
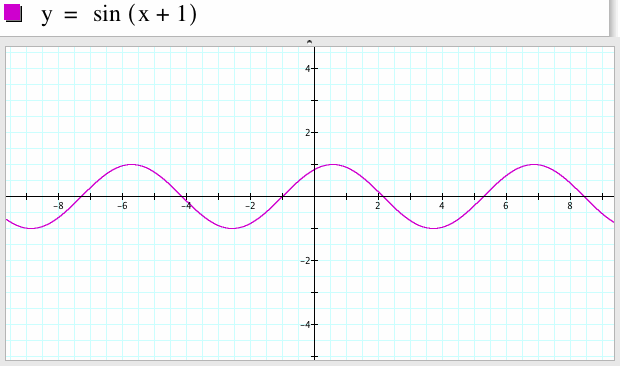
For the sine function y=sin x, the starting point of one period of the graph of the function starts at x=0. The starting point of one period of the graph of the function y=sin(x+1) starts at x=-1. Start with the graph of y=sin x, shift the graph left one unit, we get the graph of y=sin(x+1).
6. For a=1, b=1, c=-1
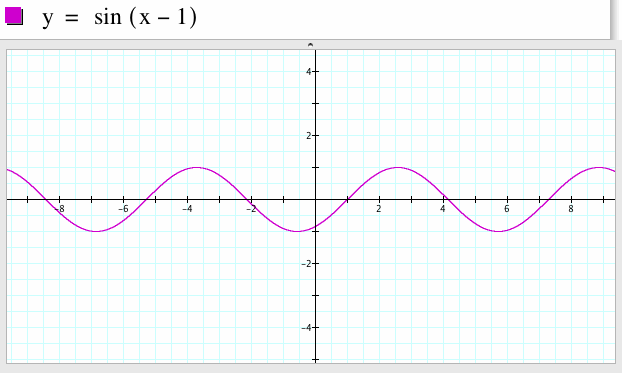
The starting point of one period of the graph of the sine function y=sin x starts at x=0. The starting point of one period of the graph of the function y=sin(x-1) starts at x=1. Start with the graph of y=sin x, shift the graph right one unit, we get the graph of y=sin(x-1). In general, from the graph of y=a sin bx, to get the graph of y=a sin(b(x+c/b)), shifts to the left c/b units if c/b>0 and shifts to the right |c/b| units if c/b<0.