

Assignment 10:
Parametric Equations
by
Wenjing Li
#3. For varoius a and b, investigate
![]()
Let us investigate the above parametric equations. First, we fix b and let a vary.
1. For a=1 and b=1
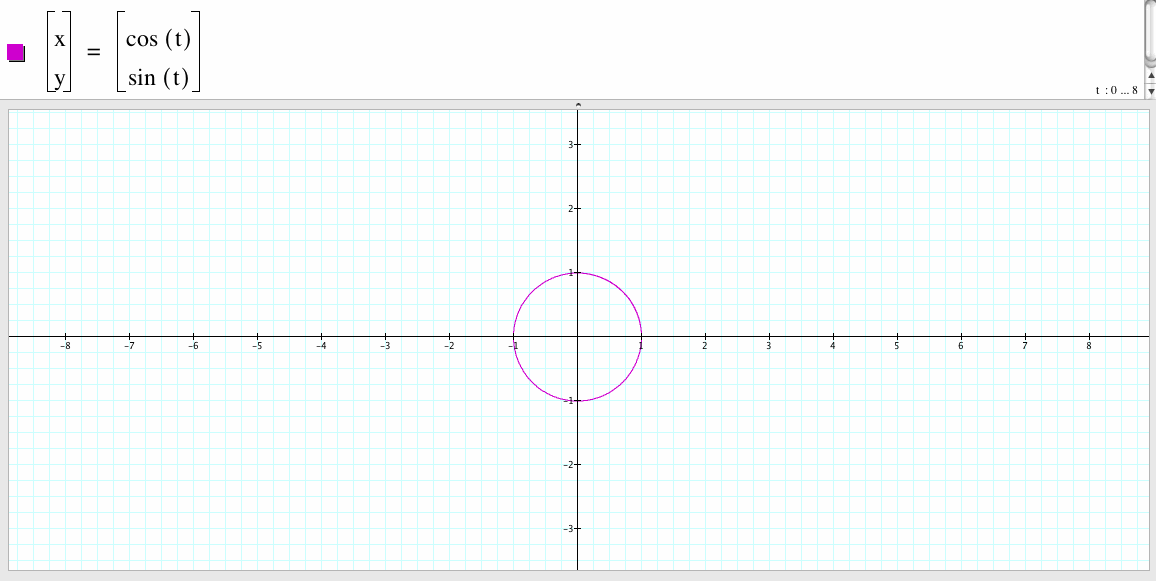
We observe that if a=1 and b=1, then the graph of the parametrized equations is a circle with center the origin point and radius 1.
2. For a=2 and b=1, we have the following graph:
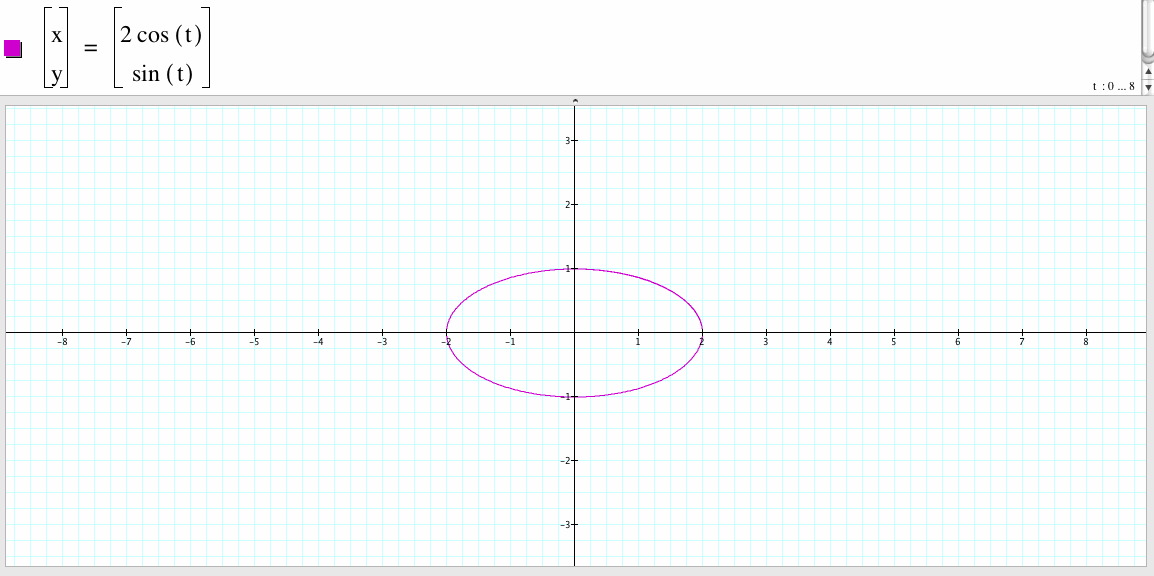
If a=2 and b=1, the graph of the parametrized equations is an ellipse with center the origin point (0 , 0), the vertex are (2,0), (-2,0), (0,1), (0,-1), the long leg with length 4 and the short leg with length 2.
3. For a=3 and b=1, we have the following graph:
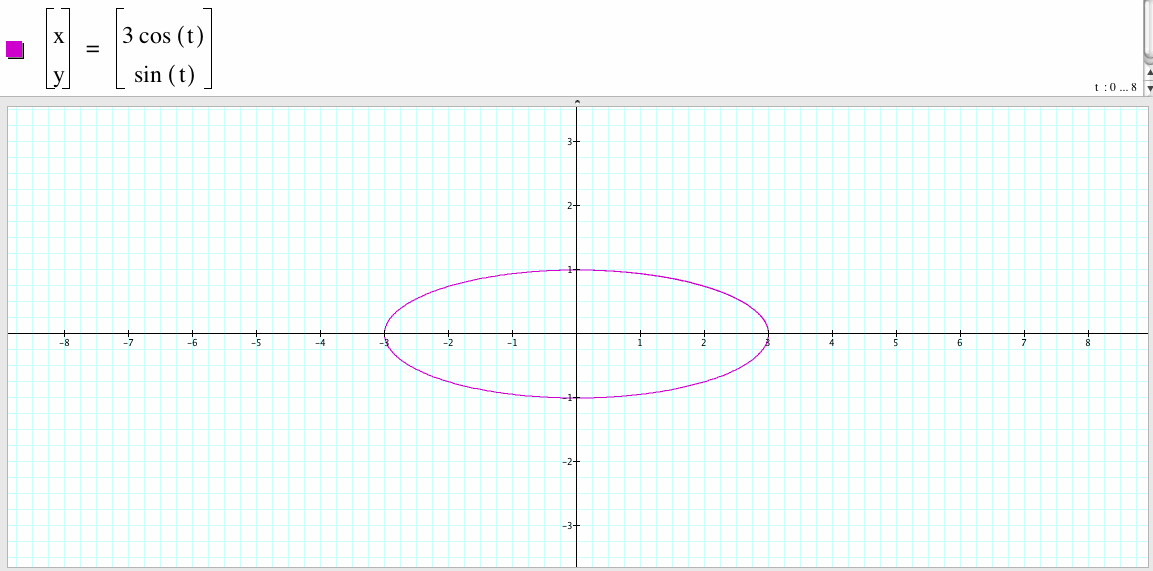
If a=3 and b=1, the graph of the parametrized equations is an ellipse with center the origin point (0 , 0), the vertex are (3,0), (-3,0), (0,1), (0,-1), the long leg with length 6 and the short leg with length 2.
Now let us fix a and let b vary.
4. For a=1 and b=2, we have the following graph:
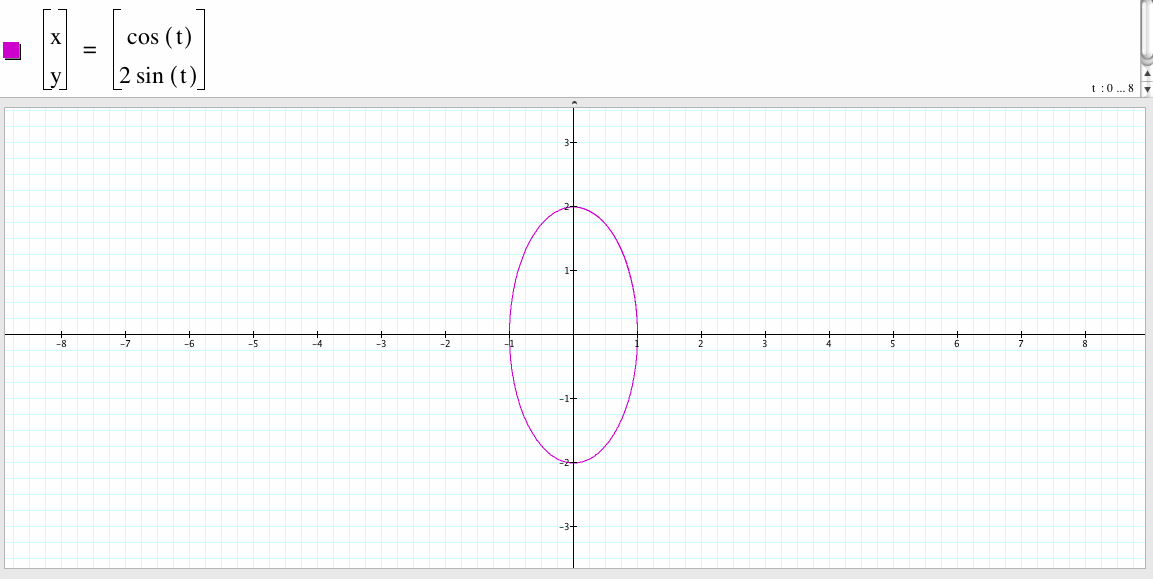
If a=1 and b=2, the graph of the parametrized equations is an ellipse with center the origin point (0 , 0), the vertex are (1,0), (-1,0), (0,2), (0,-2), the long leg with length 4 and the short leg with length 2.
5. For a=1 and b=3, we have the following graph:
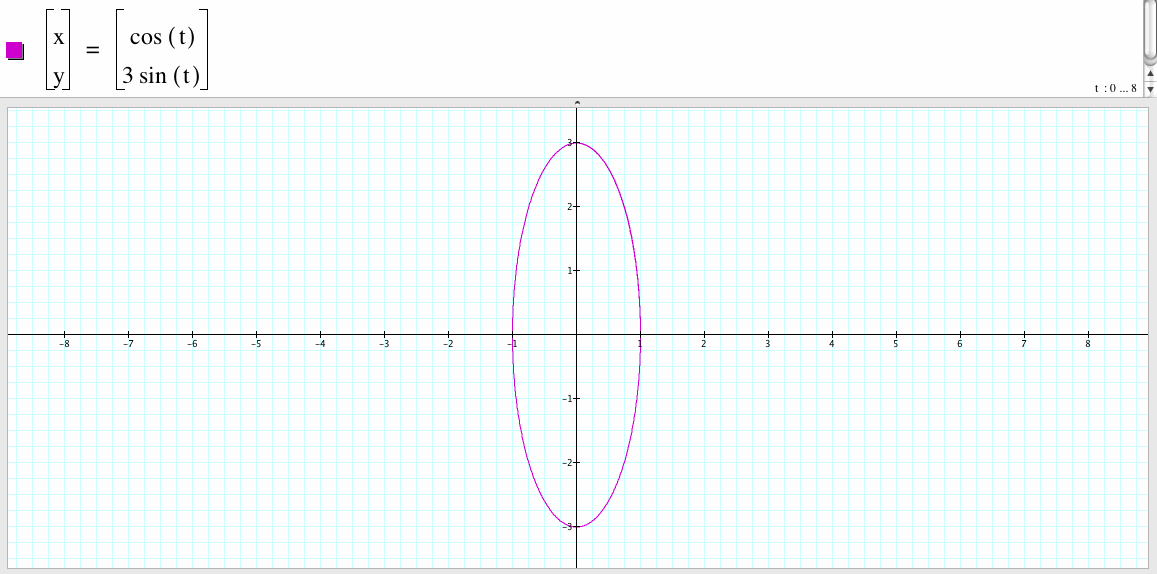
If a=1 and b=3, the graph of the parametrized equations is an ellipse with center the origin point (0 , 0), the vertex are (1,0), (-1,0), (0,3), (0,-3), the long leg with length 6 and the short leg with length 2.
Case a and b are same:
From x=a cos(t) we get cos(t)=x/a and from y=a sin(t) we get sin(t)=y/a.
By the Pythagorean trigonometry identity ![]() , we have
, we have
![]()
Simplify it, we get
![]()
which is the standard equation of the circle with center (0,0) and radius a.
Case a and b are different:
From x=a cos(t) we get cos(t)=x/a and from y=b sin(t) we get sin(t)=y/b.
By the Pythagorean trigonometry identity ![]() , we have
, we have
![]()
Simplify it, we get
![]()
which is the standard equation of the ellipse. This ellipse has center the origin point (0 , 0), the vertex are (a,0), (-a,0), (0,b), (0,-b), the long leg with length twice the absolute value of the max(a, b) and the short leg with length twice the absolute value of the min(a, b).