Assignment 11:
Polar Equations
by
Wenjing Li
1. Investigate
Note:
* When a and b are equal, and k is an integer, this is one textbook version of the " n-leaf rose."
* Compare with
for various k. What if . . . cos( ) is replaced with sin( )?
1. Let a and b be equal. For a=1, b=1 and k is an integer k=1, the graph looks like an one-leaf rose.
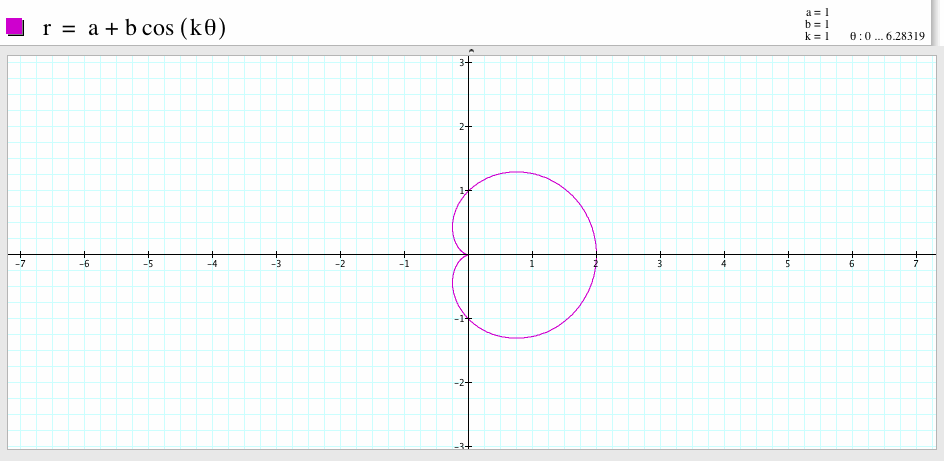
For a=1, b=1, and k=2, we get the graph which is a two-leaf rose, the two leaves are symmetric with respect to the y-axis and each leaf is symmetric with respect to the x-axis. The graph passes the points (2,0) and (-2,0).
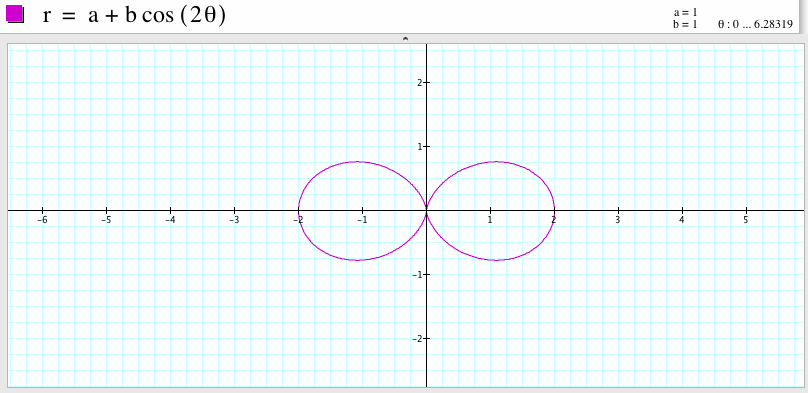
For a=1, b=1, and k=3, we get the graph which is a three-leaf rose, the graph is symmetric with respect to the x-axis. One leaf passes the point (2,0) and the other two leaves pass the points (0,1) and (0,-1) respectively.
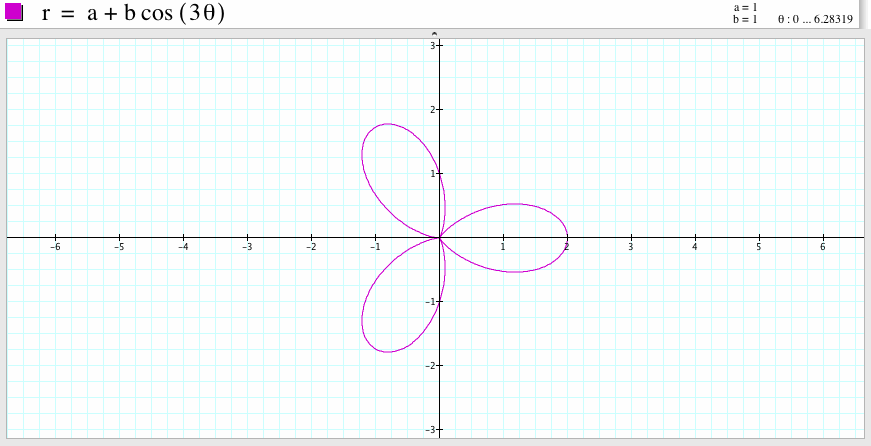
For a=1, b=1, and k=4, we get the graph which is a four-leaf rose, the graph is symmetric with respect to the y-axis and is also symmetric with respect to the x-axis. The graph passes the points (2,0), (-2,0), (0,2) and (0, -2).
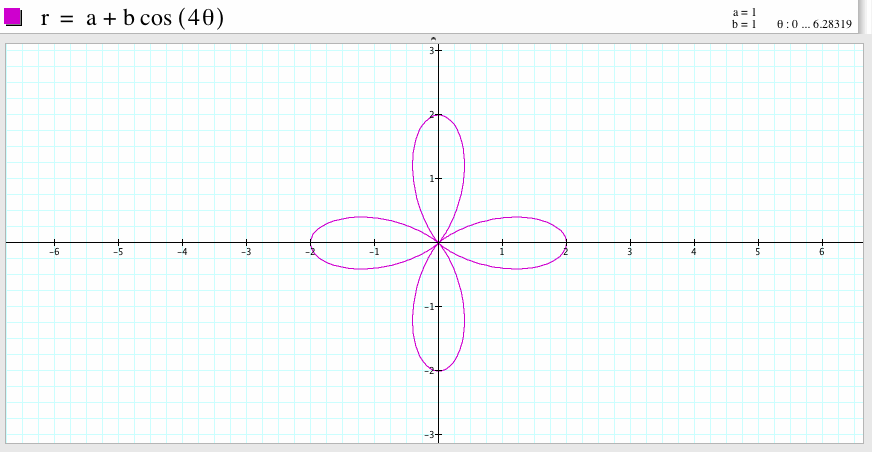
For a=1, b=1, and k=5, we get the graph which is a five-leaf rose, the graph is symmetric with respect to the x-axis. One leaf passes the point (2,0) and two leaves pass the points (0,1) and (0,-1) respectively.
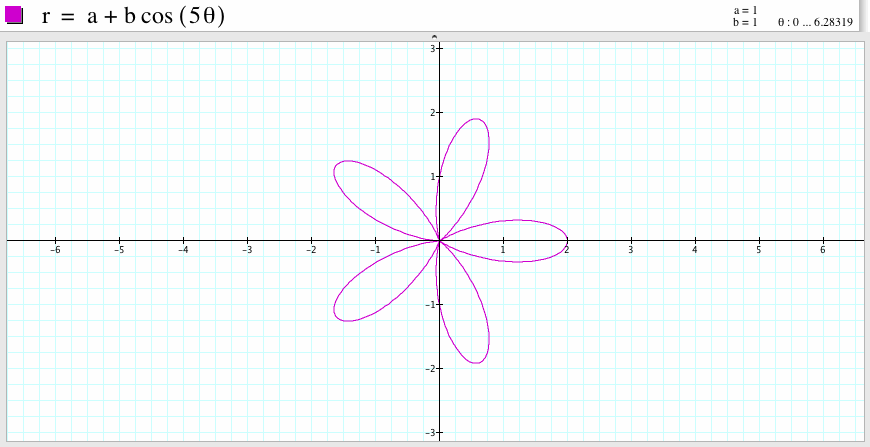
In general, if a and b are equal and k is an positive integer, the graph of the polar equation 
is a k-leaf rose which is symmetric with respect to the horizontal x-axis. There is always one leaf on the positive direction of the horizontal x-axis. If k is even, then the graph is symmetric with respect to the y-axis and is also symmetric with respect to the x-axis. If k is odd, the graph is symmetric with respect to the x-axis.
2. Let us compare with the graph of the polar equation
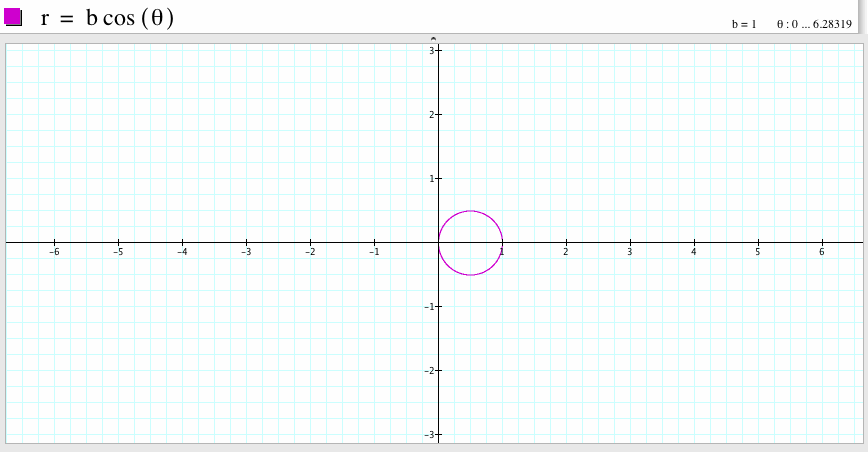
If b=1, and k=1, then the graph is a circle passes through the point (0,0) and (1,0) and has diameter 1.
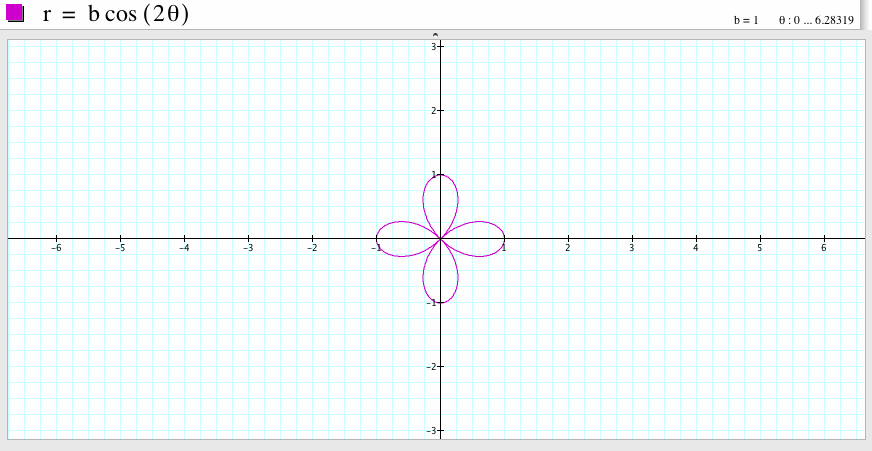
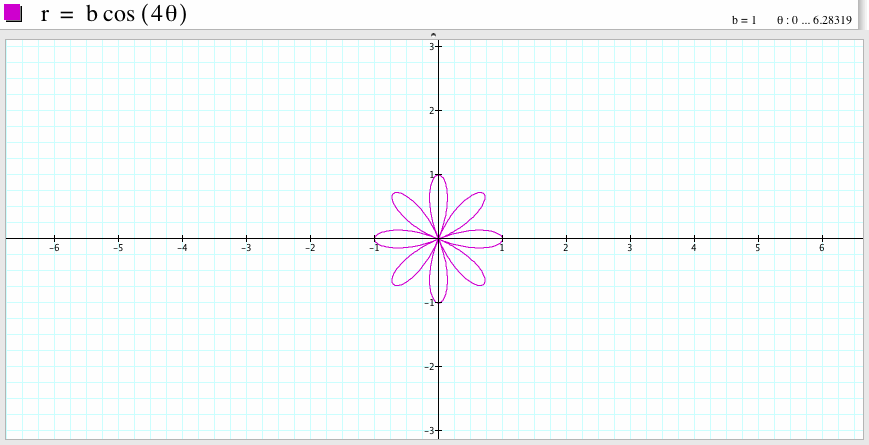
If b=1 and k=2, then the graph is a four-leaf rose. The graph is symmetric with respect to the y-axis and is also symmetric with respect to the x-axis. The graph passes the points (1,0), (-1,0), (0,1) and (0, -1).
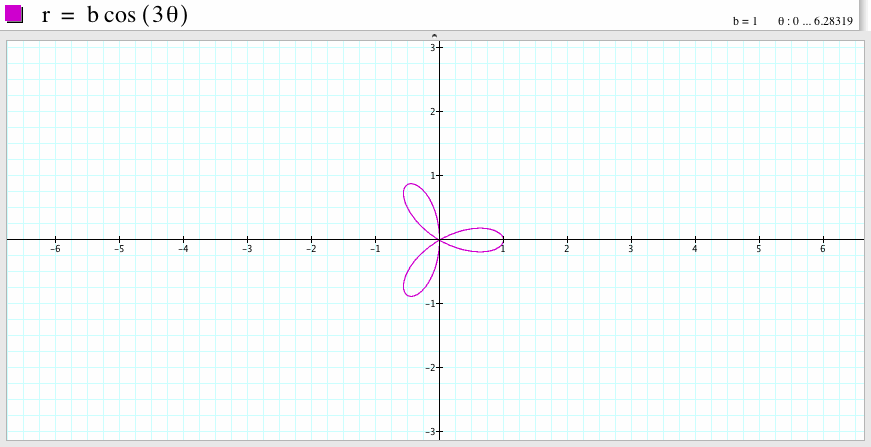
If b=1 and k=3, we get the graph which is a three-leaf rose, the graph is symmetric with respect to the x-axis. One leaf passes the point (1,0).
If b=1 and k=4, then the graph is a eight-leaf rose. The graph is symmetric with respect to the y-axis and is also symmetric with respect to the x-axis. The graph passes the points (1,0), (-1,0), (0,1) and (0, -1).
If b=1 and k=5, we get the graph which is a five-leaf rose, the graph is symmetric with respect to the x-axis. One leaf passes the point (1,0).
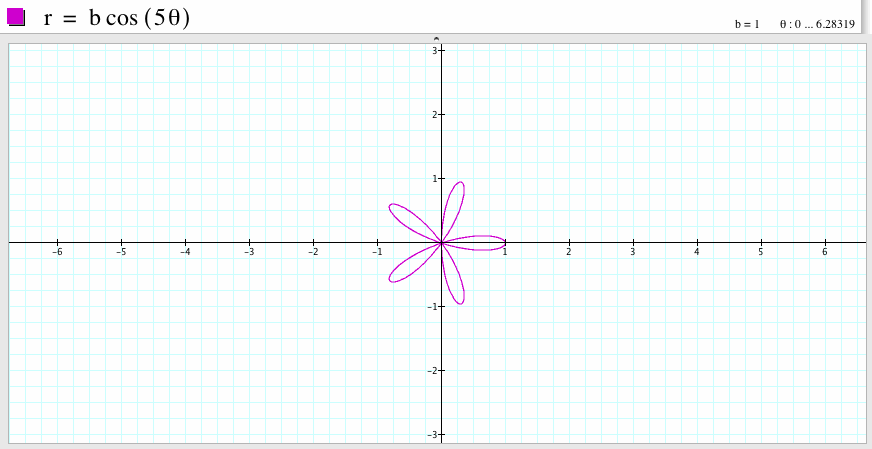
To summarize, if k is odd, then the graph of the polar equation 
is a k-leaf rose which is symmetric with respect to the horizontal x-axis. There is always one leaf on the positive direction of the horizontal x-axis. It is similar to the graph of the polar equation
which is also a k-leaf rose. If k is even, then the graph of the polar equation
is a 2k-leaf rose. If k is even, the graph of the polar equation
will have two times the number of leaves compare to the graph of the polar equation
3. Now let us investigate what will happen if we replace cos( ) with sin( ).
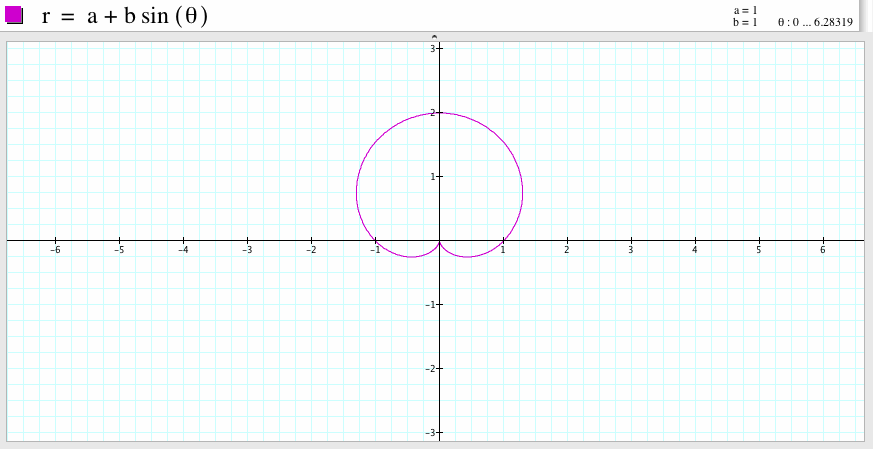
1. Let a and b be equal. For a=1, b=1 and k is an integer k=1, the graph of the polar equation
looks like an one-leaf rose. It passes through points (0,2), (1,0), (-1,0). Compare to the graph of the polar equation
if we rotate it 90 degree angle, we will get the graph of the polar equation
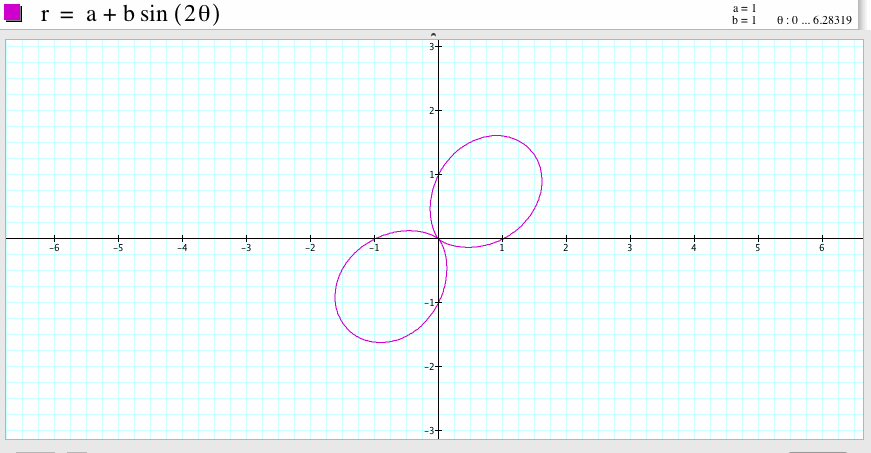
For a=1, b=1, and k=2, we get the graph which is a two-leaf rose, the two leaves are symmetric with respect to the line x=-y. The graph passes the points (1,0), (-1,0), (0, 1) (0, -1). Compare to the graph of the polar equation
if we rotate it 45 degree angle, the shape looks like the graph of the polar equation
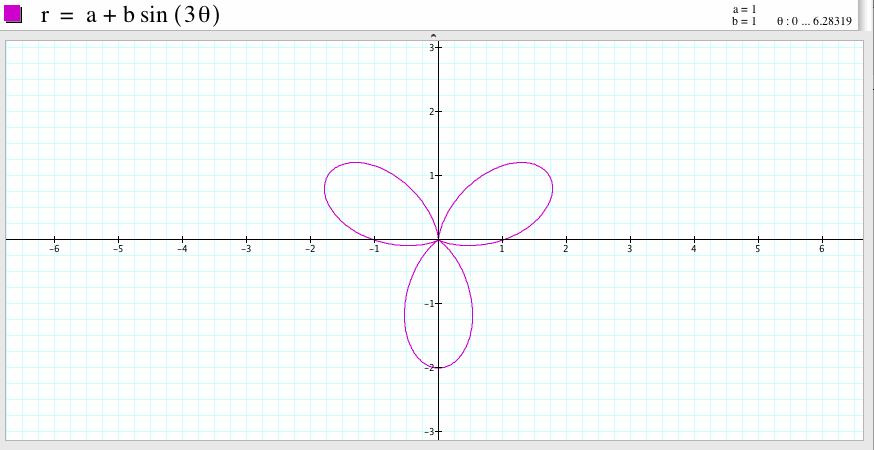
For a=1, b=1, and k=3, we get the graph which is a three-leaf rose, the graph is symmetric with respect to the y-axis. One leaf passes the point (0,-2) and the other two leaves pass the points (1,0) and (-1,0) respectively. Compare to the graph of the polar equation
if we rotate it 90 degree angle, the shape looks like the graph of the polar equation
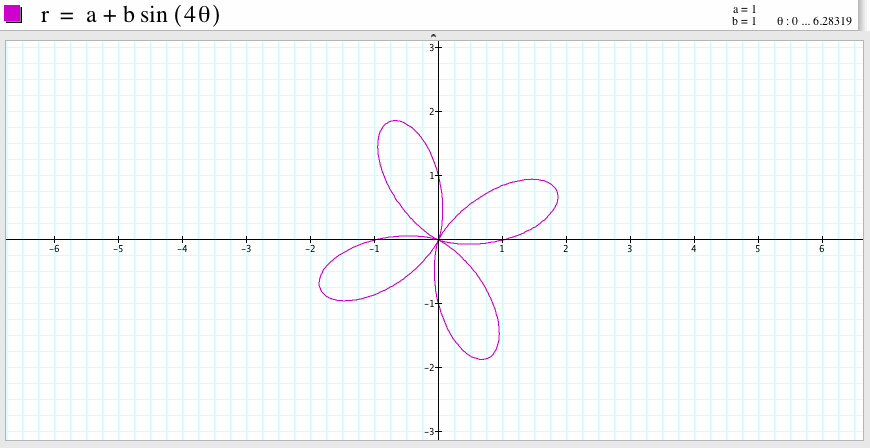
For a=1, b=1, and k=4, we get the graph which is a four-leaf rose. The graph passes the points (1,0), (-1,0), (0,1) and (0, -1). Compare to the graph of the polar equation
if we rotate it for a certain angle, the shape looks like the graph of the polar equation
In general, if a and b are equal and k is an positive integer, the graph of the polar equation
is a k-leaf rose. Compare to the graph of the polar equation
if we rotate it for a certain angle, the shape looks like the graph of the polar equation
4. Let us compare with the graph of the polar equation
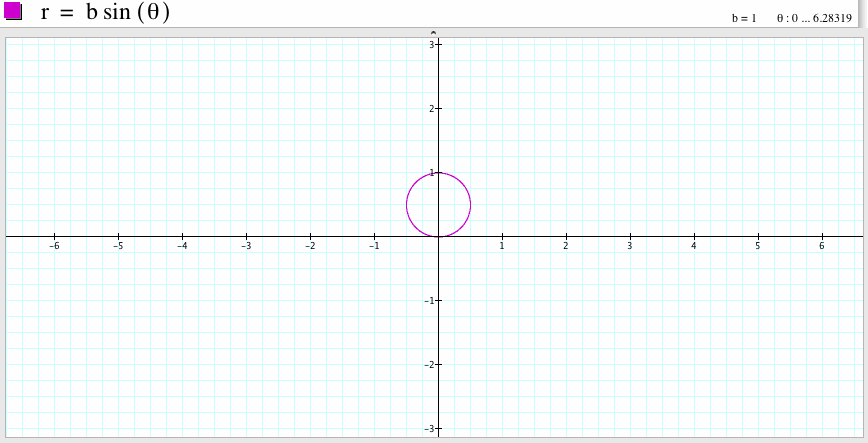
If b=1, and k=1, then the graph is a circle passes through the point (0,0) and (0,1) and has diameter 1.
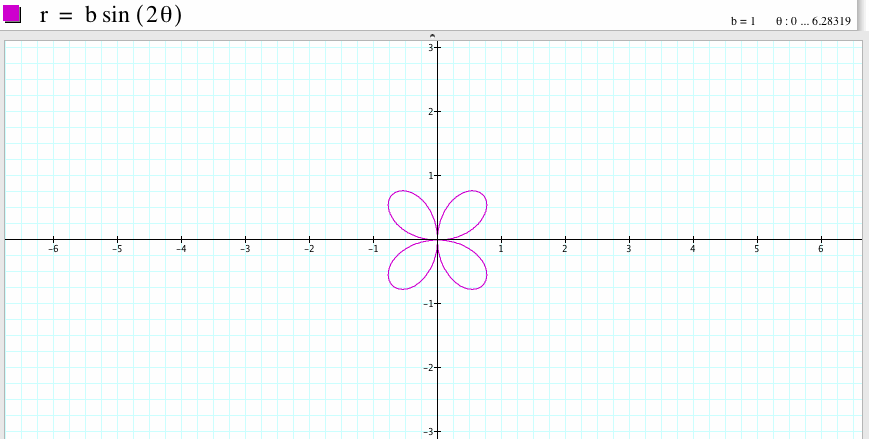
If b=1 and k=2, then the graph is a four-leaf rose. The graph is symmetric with respect to the y-axis and is also symmetric with respect to the x-axis. Compare to the graph of the polar equation
if we rotate it 45 degree angle, the shape looks like the graph of the polar equation
If b=1 and k=3, we get the graph which is a three-leaf rose, the graph is symmetric with respect to the y-axis. One leaf passes the point (0,-1). Compare to the graph of the polar equation
if we rotate it 90 degree angle, the shape looks like the graph of the polar equation
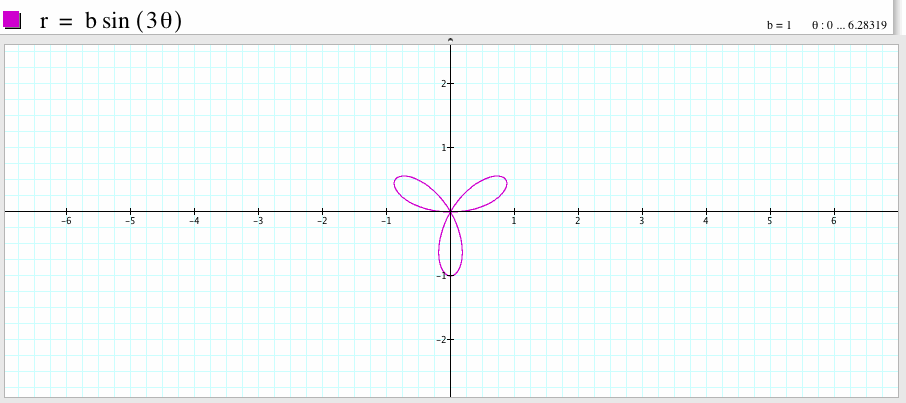
If b=1 and k=4, then the graph is a eight-leaf rose. The graph is symmetric with respect to the y-axis and is also symmetric with respect to the x-axis. Compare to the graph of the polar equation
if we rotate it for a certain angle, the shape looks like the graph of the polar equation
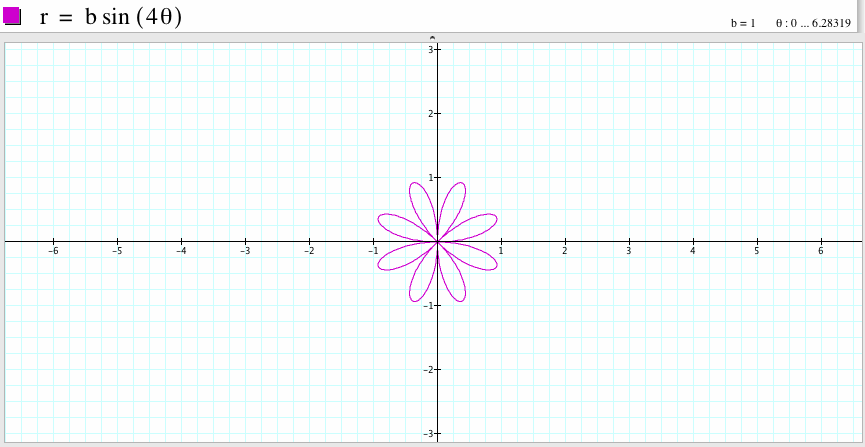
To summarize, if k is odd, then the graph of the polar equation
is a k-leaf rose. It is similar to the graph of the polar equation
which is also a k-leaf rose. If k is even, then the graph of the polar equation
is a 2k-leaf rose. If k is even, the graph of the polar equation
will have two times the number of leaves compare to the graph of the polar equation
Compare to the graph of the polar equation , if we rotate it for a certain angle, the shape looks like the graph of the polar equation