

Assignment 12:
The Spreadsheet in Mathematics Explorations
by
Wenjing Li
4. Generate a Fibonnaci sequence in the first column using f(0) = 1, f(1) = 1,
f(n) = f(n-1) + f(n-2).
a. Construct the ratio of each pair of adjacent terms in the Fibonnaci sequence. What happens as n increases? What about the ratio of every second term? etc.
b. Explore sequences where f(0) and f(1) are some arbitrary integers other than 1. If f(0)=1 and f(1) = 3, then your sequence is a Lucas Sequence. All such sequences, however, have the same limit of the ratio of successive terms.
Let us generate Fibonnaci sequence using the Spreadsheet.
a. If we let the first column start with f(0)=1 and f(1)=1 and let f(n)=f(n-1) + f(n-2), then we get the following Fibonnaci sequence. We construct the ratio of each pair of adjacent terms in the Fibonnaci sequence, we have f(1)/f(0)=1, f(2)/f(1)=2, f(3)/f(2)=1.5, f(4)/f(3)= 1.66666667, ...... If n increases, then the ratio f(n+1)/f(n) approaches to 1.61803399. Let us investigate the ratio of the every second term, f(2)/f(0)=2, f(3)/f(1)=3, f(4)/f(2)=2.5, f(5)/f(3)=2.66666667, ...... If n increases, then the ratio f(n+2)/f(n) approaches to 2.61803399. For the ratio of the every third term, f(3)/f(0)=3, f(3)/f(1)=5, f(4)/f(2)=4, f(5)/f(3)=4.33333333, ...... If n increases, then the ratio f(n+3)/f(n) approaches to 4.23606798. In general, for the ratio of the every kth term, as n increases, the ratio f(n+k)/f(n) always approaches to a limit.
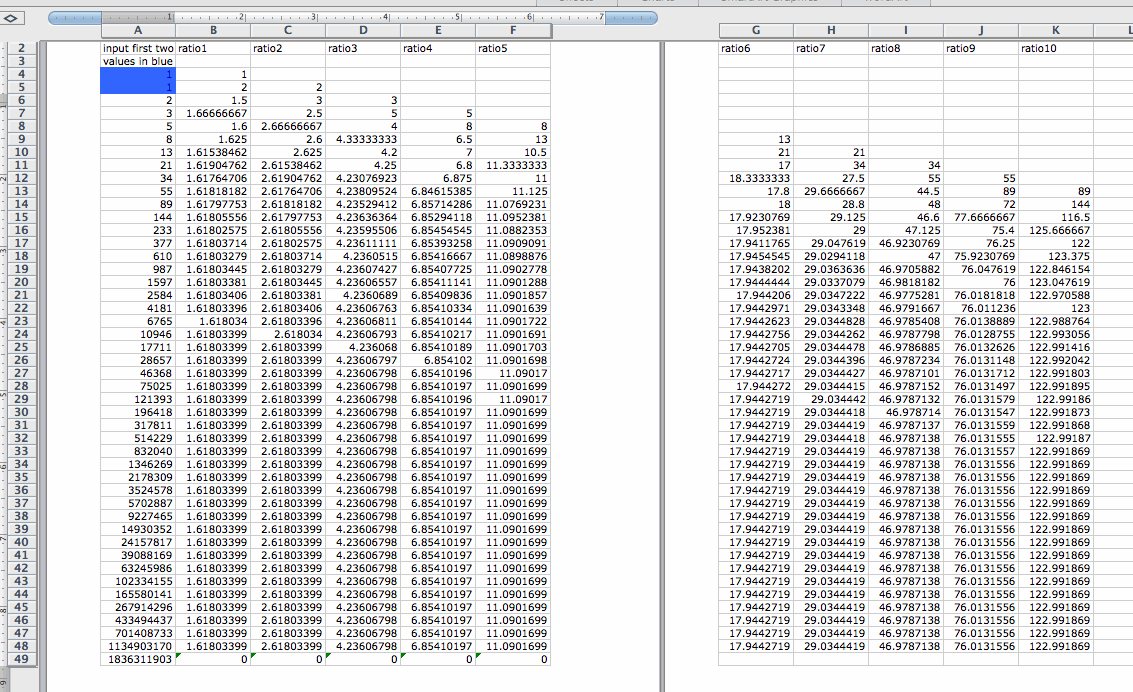
b. Let us explore sequences where f(0) and f(1) are some arbitrary integers other than 1. If we let f(0)=1 and f(1) = 3 and let f(n)=f(n-1) + f(n-2), then we get the following sequence which is called a Lucas Sequence. Let us construct the ratio of each pair of adjacent terms in the Lucas Sequence, we have f(1)/f(0)=3, f(2)/f(1)=1.33333333, f(3)/f(2)=1.75, f(4)/f(3)= 1.57142857, ...... If n increases, then the ratio f(n+1)/f(n) approaches to 1.61803399. Now we investigate the ratio of the every second term, f(2)/f(0)=4, f(3)/f(1)=2.33333333, f(4)/f(2)=2.75, f(5)/f(3)=2.57142857, ...... If n increases, then the ratio f(n+2)/f(n) approaches to 2.61803399. For the ratio of the every third term, f(3)/f(0)=7, f(3)/f(1)=3.66666667, f(4)/f(2)=4.5, f(5)/f(3)=4.14285714, ...... If n increases, then the ratio f(n+3)/f(n) approaches to 4.23606798. In general, for the ratio of the every kth term, as n increases, the ratio f(n+k)/f(n) always approaches to a limit. We compare this Lucas Sequence with the previous Fibonnaci sequence, then we found out that these two sequences have the same limit of the ratio of successive terms as n increases.
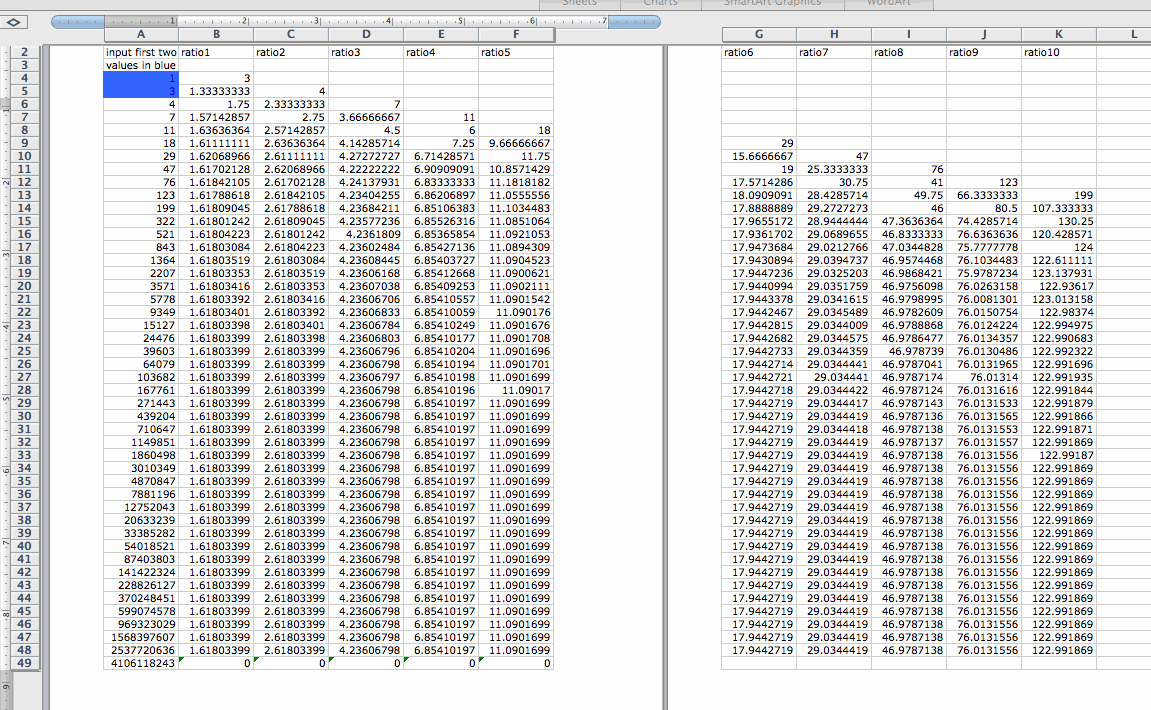
What will happen if the sequence start with other integers? Now we let f(0)=2 and f(1) = 5 and let f(n)=f(n-1) + f(n-2), then we get the following sequence. We construct the ratio of each pair of adjacent terms in the sequence, we have f(1)/f(0)=2.5, f(2)/f(1)=1.4, f(3)/f(2)=1.71428571, f(4)/f(3)= 1.58333333, ...... If n increases, then the ratio f(n+1)/f(n) approaches to 1.61803399. For the ratio of the every second term, f(2)/f(0)=3.5, f(3)/f(1)=2.4, f(4)/f(2)=2.71428571, f(5)/f(3)=2.583333333, ...... If n increases, then the ratio f(n+2)/f(n) approaches to 2.61803399. We construct the ratio of the every third term, f(3)/f(0)=6, f(3)/f(1)=3.8, f(4)/f(2)=4.2857143, f(5)/f(3)=4.16666667, ...... If n increases, then the ratio f(n+3)/f(n) approaches to 4.23606798.
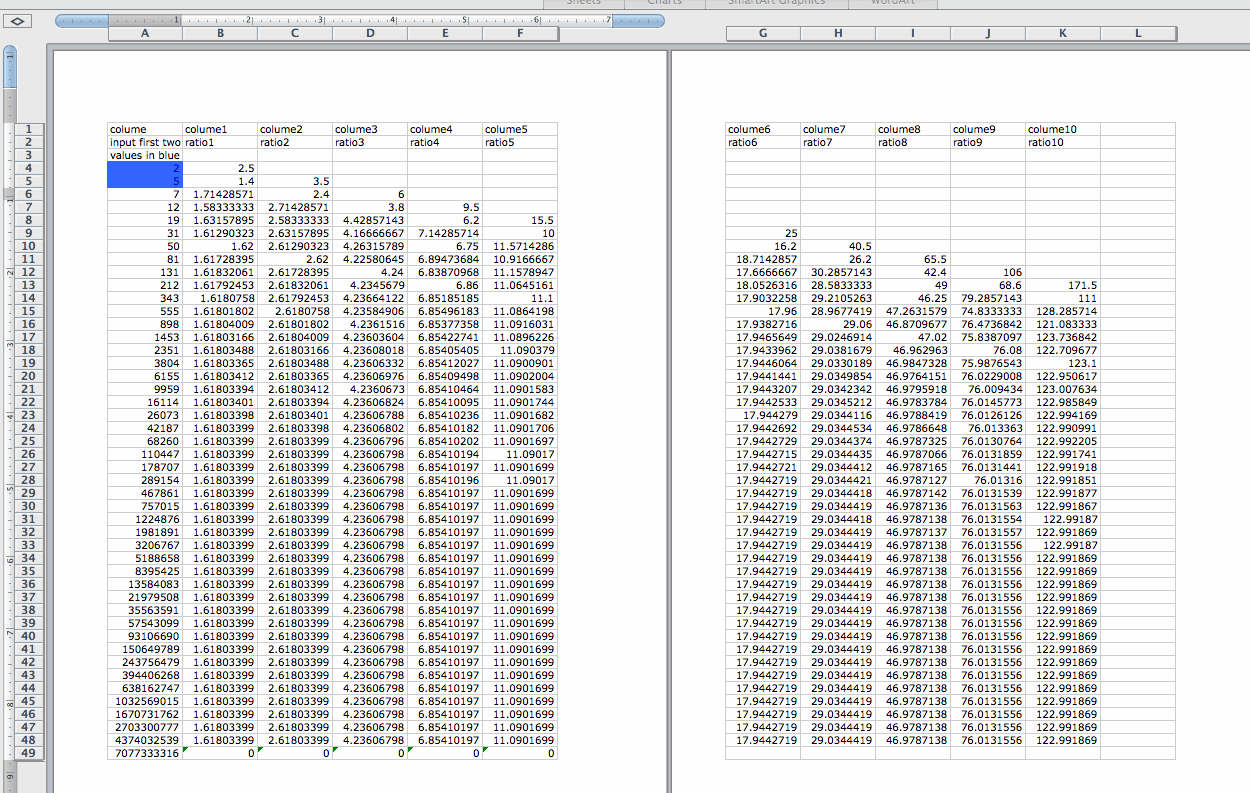
We will try another case. Let us start with f(0)=3 and f(1) = 8 and let f(n)=f(n-1) + f(n-2), then we get the following sequence. And we construct the ratio of each pair of adjacent terms in the sequence, we have f(1)/f(0)=2.66666667, f(2)/f(1)=1.375, f(3)/f(2)=1.72727273, f(4)/f(3)= 1.57894737, ...... If n increases, then the ratio f(n+1)/f(n) approaches to the same value 1.61803399. For the ratio of the every second term, f(2)/f(0)=3.666666667, f(3)/f(1)=2.375, f(4)/f(2)=2.72727273, f(5)/f(3)=2.57894737, ...... If n increases, then the ratio f(n+2)/f(n) approaches to 2.61803399. We construct the ratio of the every third term, f(3)/f(0)=6.33333333, f(3)/f(1)=3.75, f(4)/f(2)=4.4545454545, f(5)/f(3)=4.15789474, ...... If n increases, then the ratio f(n+3)/f(n) approaches to 4.23606798. In general, for the ratio of the every kth term, as n increases, the ratio f(n+k)/f(n) always approaches to a limit. We compare this sequence with the previous three sequences and found out that all the sequences that we investigate have the same limit of the ratio of successive terms as n increases. The limit of the ratio of successive terms does not depend on the first two terms f(0) and f(1) that we start with.
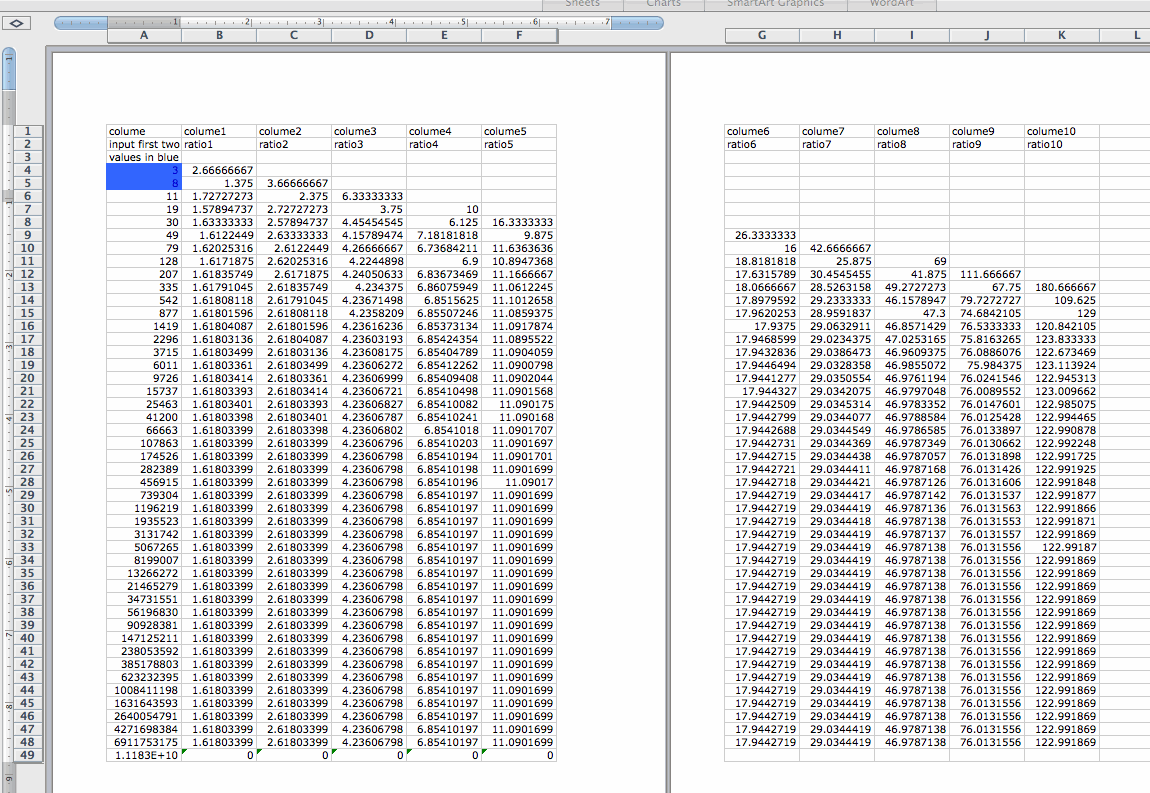
We investigate the limit of the ratio of each pair of adjacent terms in the Fibonnaci sequence
Let f(0)= 1, f(1)=1
f(n+1) = f(n) + f(n-1)
then the ratio
f(n+1)/f(n) =(f(n) + f(n-1))/f(n)
let lim (f(n+1)/f(n))=L
then we have
L=1+1/L
multiply both side by L, we get
![]()
then we have the following equation
![]()
We solve the equation using the quatratic formular and get the solutions
![]()
We choose the positive solution
![]()
Let us recall the golden ratio. Two quantities a and b are in golden ratio if the ratio of the sum of the quantities to the larger one equals the ratio of the larger one to the smaller.
(a+b)/a=a/b
Let x=a/b which is the golden ratio, then we have
1+1/x=x
multiply both sides by x, we get
![]()
solve this equation and we find that the golden ratio x is
![]()
which is the same as the limit that we found lim (f(n+1)/f(n))=L which is
![]()
approximately equal to 1.618 as we observed that the ratio of each pair of adjacent terms in the above sequences in the first column approches to 1.61803399 as n approches to infinity.