

Assignment 2:
Parabola
by
Wenjing Li
#1. Examine graphs for the parabola y=ax^2+bx+c for different values of a, b, and c. (a, b, c can be any rational numbers).
Try using the GC animation by replacing a, b, or c with an n and selecting an appropriate range for n.
Let us examine the graph of the parabola.
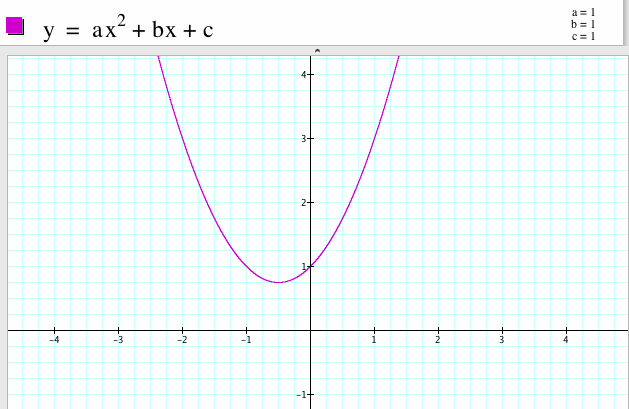
We can rewrite the equation of the parabola into another form.
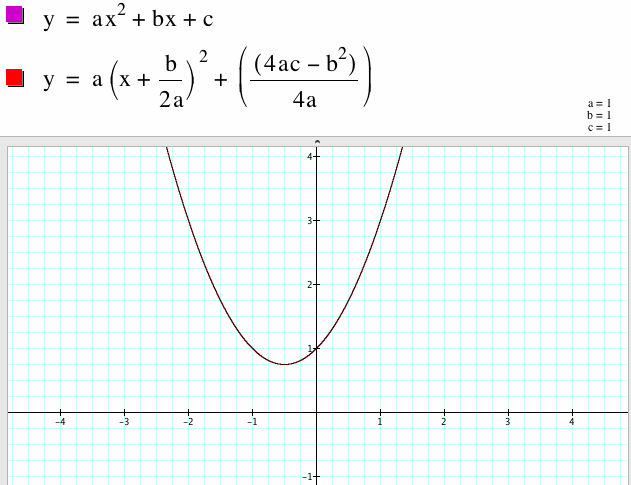
We examine the graphs for the parabola for different values of a.
1. For a=1, b=0, c=0
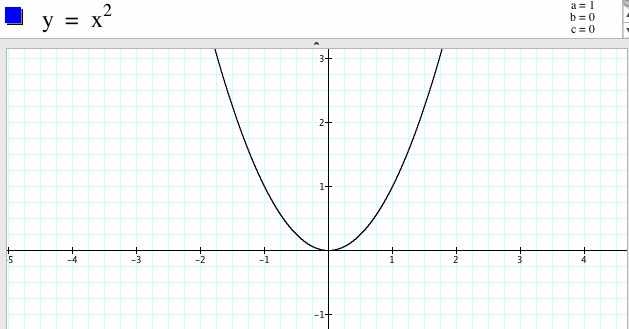
The parabola opens up and the vertex of it is the point (0,0).
What will happen if the leading coefficient is negative? Let us examine the graph of the parabola when a=-1, b=0 and c=0.
2. For a=-1, b=0, c=0
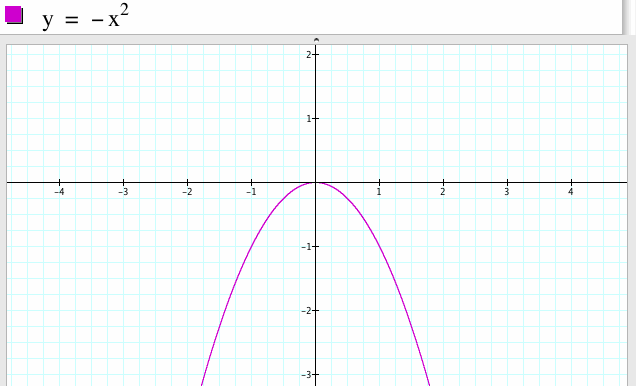
If the leading coefficient is negative, then the graph of the parabola is open down. To generalize this, if the leading coefficient is positive, then the graph of the parabola opens up and if the leading coefficient is negative, then the graph of the parabola opens down. So the sign of the leading coefficient determines the direction of the parabola opens. We also see that this parabola has the vertex at the point (0.0).
3. For a=2, b=0, c=0
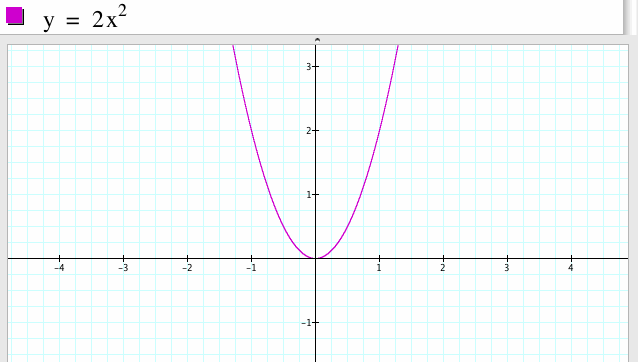
The graph of the parabola opens narrower than the previous one. In general, the smaller the absolute value of the leading coefficient is, the wider the graph of the parabola opens and the bigger the absolute value of the leading coefficient is, the narrower the graph of the parabola opens. Thus the absolute value of the leading coefficient determines the wideness of the graph of the parabola opens. This parabola has the same vertex point (0.0).
Now we examine the graphs for the parabola for different values of b.
4. For a=1, b=2, c=0
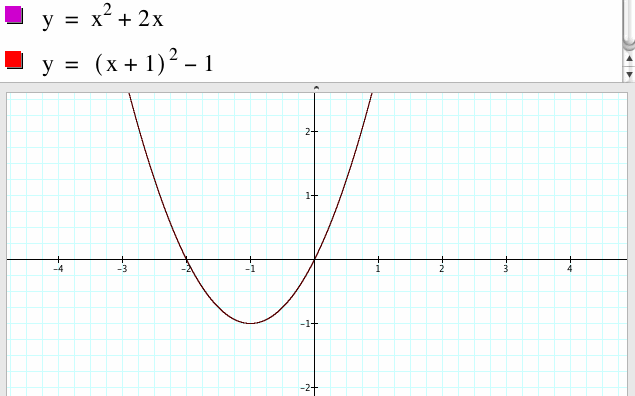
The graph of this parabola has the line of x=-1, the vertex of it is the point (-1,-1) and it opens up.
5. For a=1, b=-2 and c=0
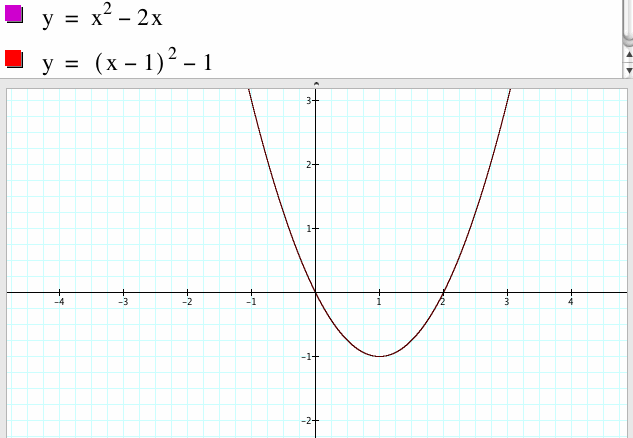
The graph of this parabola has the line of x=1, the vertex of it is the point (1,-1) and it opens up. We generalize this, the line of symmetry of the general form parabola is x=-b/2a. If we fix a and let b vary, then the line of the symmetry will change.
What will happen to the graphs for the parabola if c has different values?
6. For a=1, b=2 and c=1
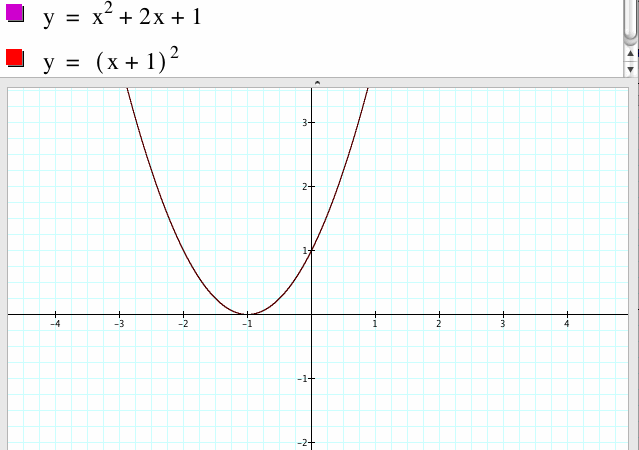
The graph of this parabola has vertex at the point (-1, 0), the line of symmetry x=-1 and it opens up.
7. For a=1, b=2 and c=-2
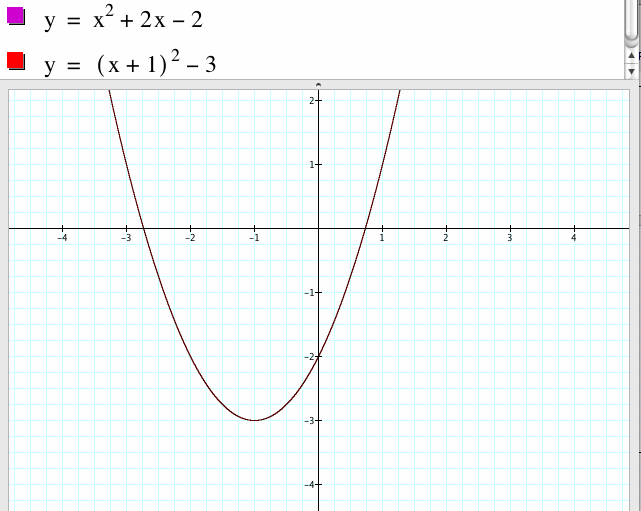
The graph of this parabola has vertex at the point (-1, -3), the line of symmetry x=-1 and it opens up. The graph of this parabola moves down compares to the previous one. We can generalize this, the vertex of the general form parabola is (-b/2a, (4ac-b^2)/4a), so if we fix the coefficient of a and b and let c vary, then the vertex of the parabola will have different y-coordinate. If c becomes bigger, then the graph of the parabola will move up, and if c becomes smaller, then the graph of the parabola will move down. The bigger c is, the upper the graph of the parabola will move to and the smaller c is, the downer the graph of the parabola will move to.
To summarize, the graph of the general form parabola has line of symmetry x=-b/2a , it has the vertex (-b/2a, (4ac-b^2)/4a) and if the absolute value of the leading coefficient is positive, it opens up and if the absolute value of the leading coefficient is negative, it opens down.
Lets examine the animation of the graph of the parabola by replacing the coefficients a, b, or c with n and select an appropriate range for n.
8. We replace a with n and select the range for n to be [-5,5].
From the animation we see that if we fix b and c, replace a with n and select the range for n to be [-5, 5], then the parabola will animate from opens up to opens down, but the graph of this family of parabolas are always passing through the point (0,1) on the y-axis. This shows that the sign of the leading coefficient determines whether the parabola opens up or down and the absolute value of the leading coefficient determines how wide the parabola opens.
9. We replace b with n and select the range for n to be [-5,5].
From this animation we see that if we fix a and c, replace b with n and select the range for n to be [-5, 5], then the vertex of the parabola will move from the third quadrant to the second quadrant, to the first quadrant and then to the fourth quadrant, and the graph of this family of parabolas are always passing through the point (0,1) on the y-axis.
10. We replace c with n and select the range for n to be [-3,3].
From this animation we see that if we fix a and b, replace c with n and select the range for n to be [-3, 3], then the parabola will move up and down. If a and b are fixed, then the value of c will determine the y-coordinate of the vertex.