

Assignment 3:
Quadratic and Cubic Equations
by
Wenjing Li

can be followed.
1. We set y=a x^2+x+1 for a = -3, -2, -1, 0, 1, 2, 3, and overlay the graphs, the following picture is obtained.
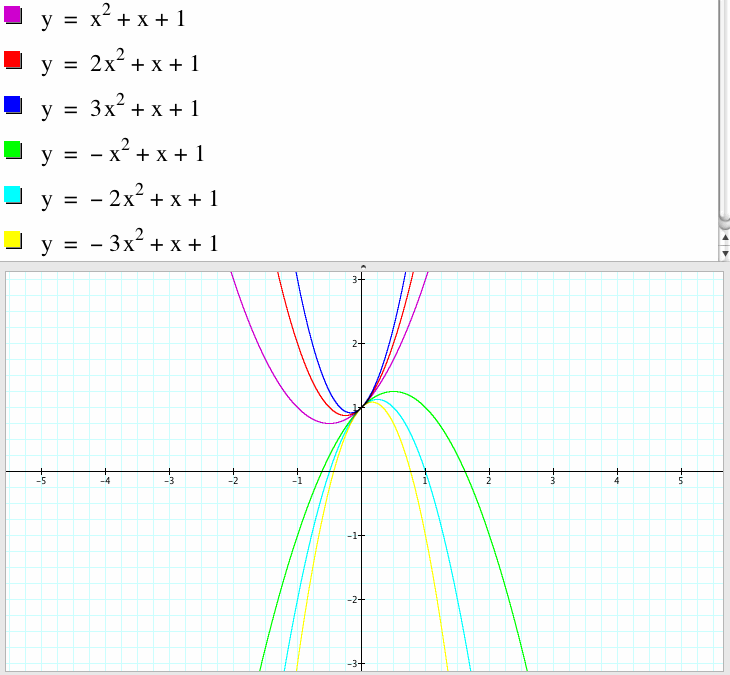
This family of parabolas always pass the point (0,1) on the y-axis. When the leading coefficient is positive, the parabola opens up and when the leading coefficient is negative, the parabola opens down.
2. We set y=x^2+bx+1
for b = -3, -2, -1, 0, 1, 2, 3, and overlay the graphs, then we abtain the following graphs.
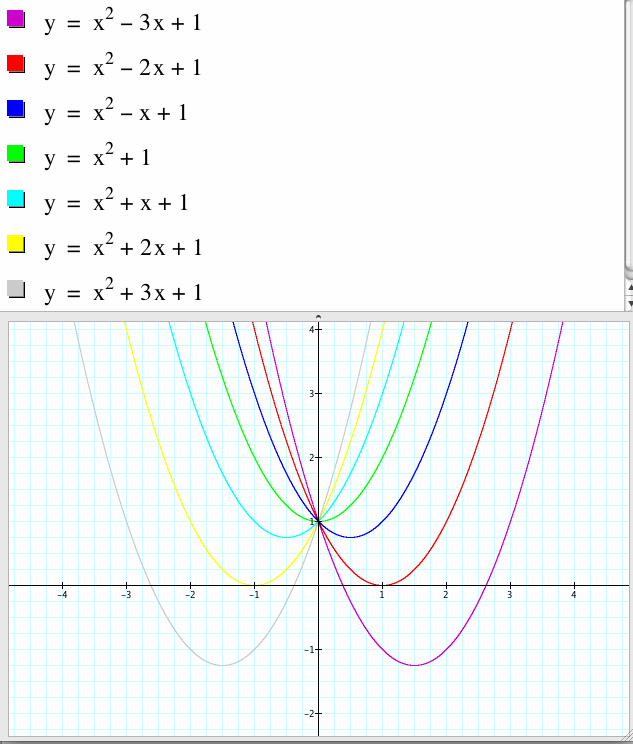
Let us investigate the movement of a parabola as b is changed and a, b are fixed. From the graph we see that the parabola always passes through the same point (0, 1) on the y-axis. For b > 2, the parabola intersects the x-axis at two points and there are two negative real roots. For b = 2 the parabola is tangent to the x-axis and it has one real negative root. For -2 < b < 2, the parabola does not intersect the x-axis and so the original equation has no real roots. For b = -2, the parabola is tangent to the x-axis and the original equation has one real and positive root at the point of tangency. For b < -2 the parabola will intersect the x-axis in two points with positive x values and the original equation will have two real roots which are both positive.
Now consider the locus of the vertices of the set of parabolas.
We show that the locus is a parabola.
y=x^2+bx+(b/2)^2+1-(b/2)^2
Complete the square, we get
y=(x+b/2)^2+1-(b/2)^2
Let the vertex point to be (s, t), then
s=-b/2 and t=1-(b/2)^2
The x-coordinate s and the y-coordinate t of the vertex point satisfy the equation s^2+t=0, which is an equation of a parabola. Hence the locus is a parabola.
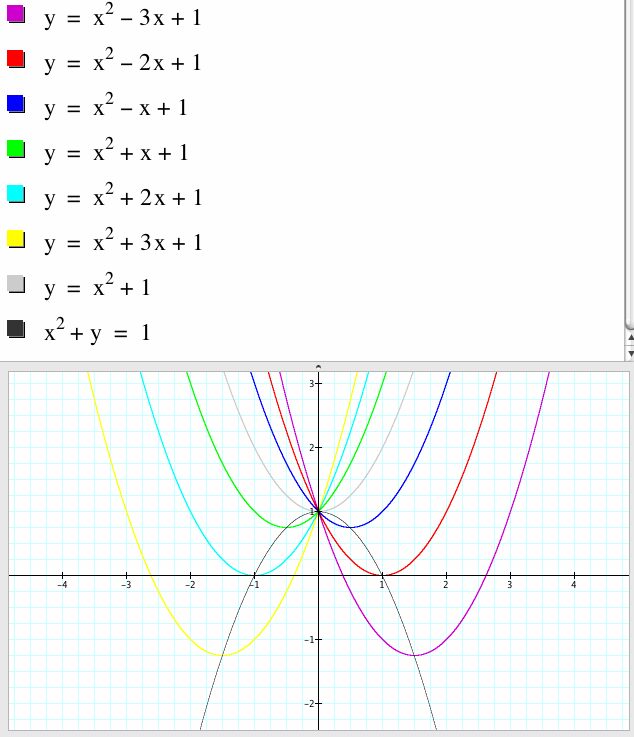
3. We set y= x^2+x+c
for c = -3, -2, -1, 0, 1, 2, 3, and overlay the graphs, and obtain the following graphs.
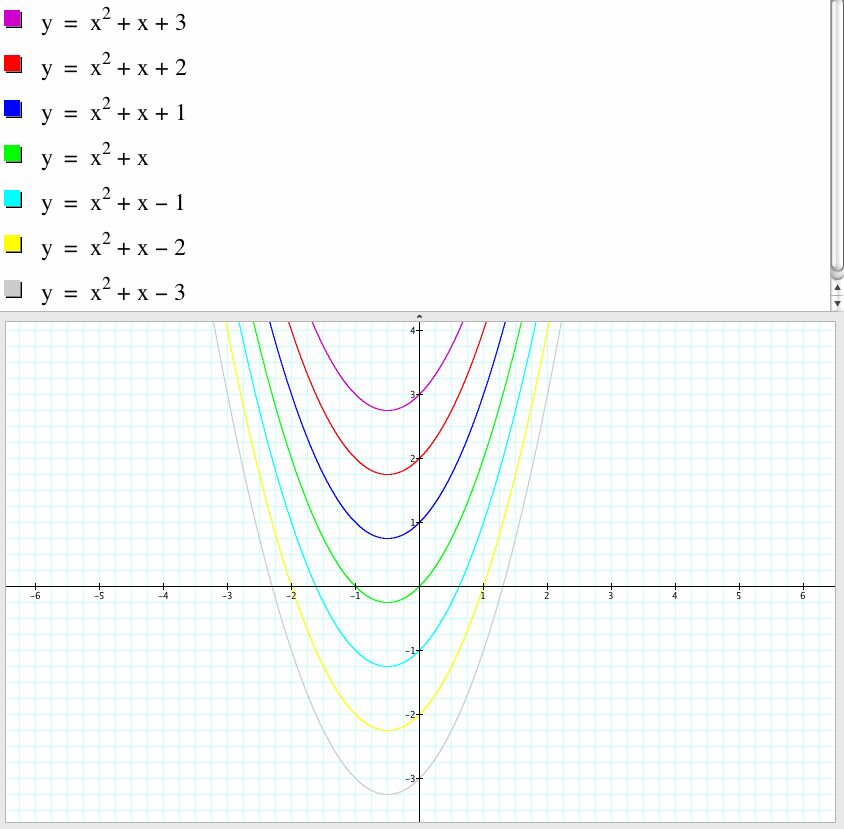
If we fix a and b let c vary, then the graph of the parabola moves up and down and they have the same shape.
Investigation 2.
Graphs in the xb plane.
Consider again the equation
Now graph this relation in the xb plane.
If we take any particular value of b, say b = 5, and overlay this equation on the graph we add a line parallel to the x-axis. If it intersects the curve in the xb plane the intersection points correspond to the roots of the original equation for that value of b. We have the following graph.
For each value of b we select, we get a horizontal line. It is clear on a single graph that we get two negative real roots of the original equation when b > 2, one negative real root when b = 2, no real roots for -2 < b < 2, One positive real root when b = -2, and two positive real roots when b < -2.
Consider the case when c = - 1 rather than + 1.
Graph other values of c on the same axes.
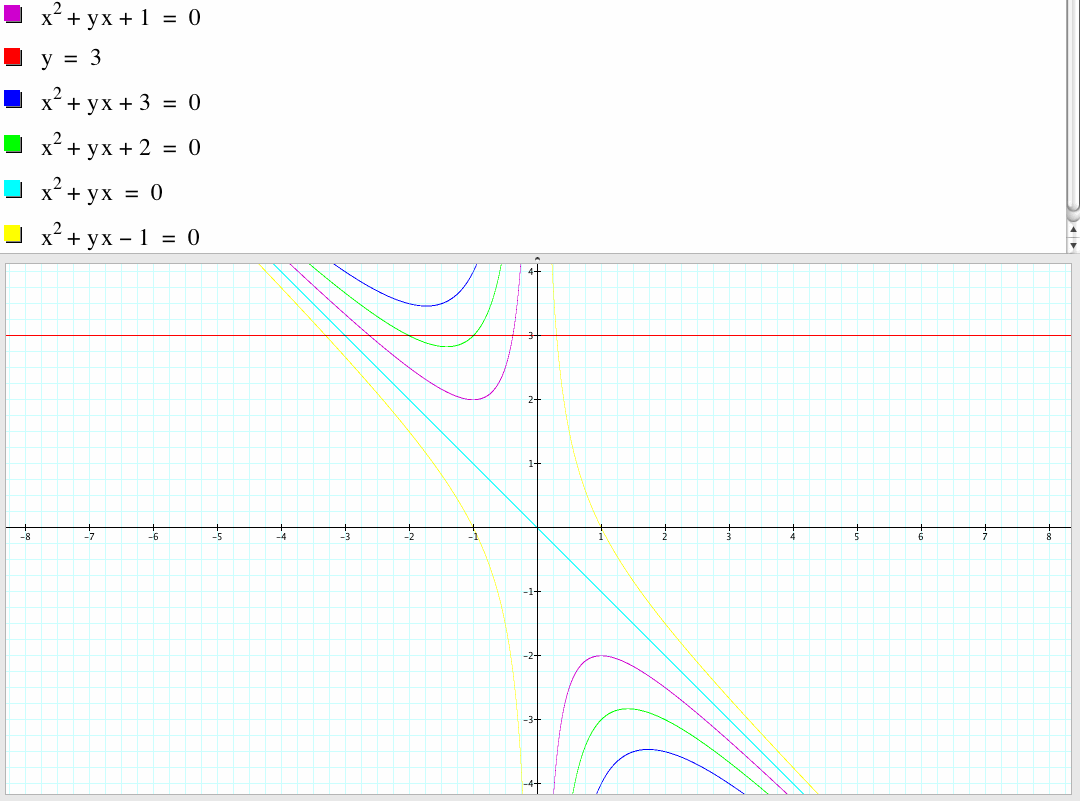
We take any particular value of b=3 and overlay this equation on the graph then we add a line parallel to the x-axis. If it intersects the curve in the xb plane the intersection points correspond to the roots of the original equation for this value of b. For each value of b we will get a horizontal line. We get two negative real roots of the original equation when b > 2, one negative real root when b = 2, no real roots for -2 < b < 2, one positive real root when b = -2, and two positive real roots when b < -2. When c = - 1, the graph is the yellow curve and it always intersects the red horizontal line at two points.
Investigation 3.
Add the graph of 2x + b = 0 to the picture and discuss its relation to the quadratic formula.
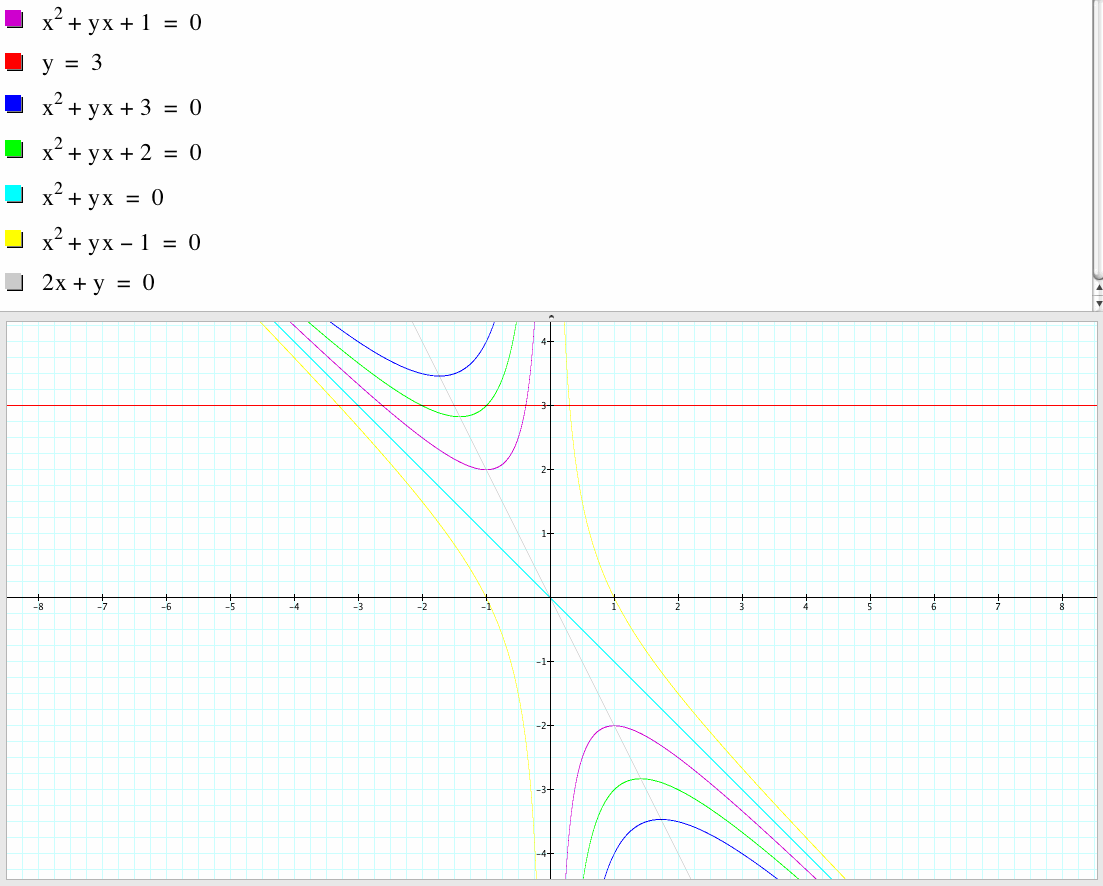
If we add the graph of 2x + b = 0 to the picture we will get the above graphs. We see that if we connect the vertex of this family of parabolas, it is the line 2x+b=0 that we add.
Investigation 4.
Consider graphs in the xc plane.
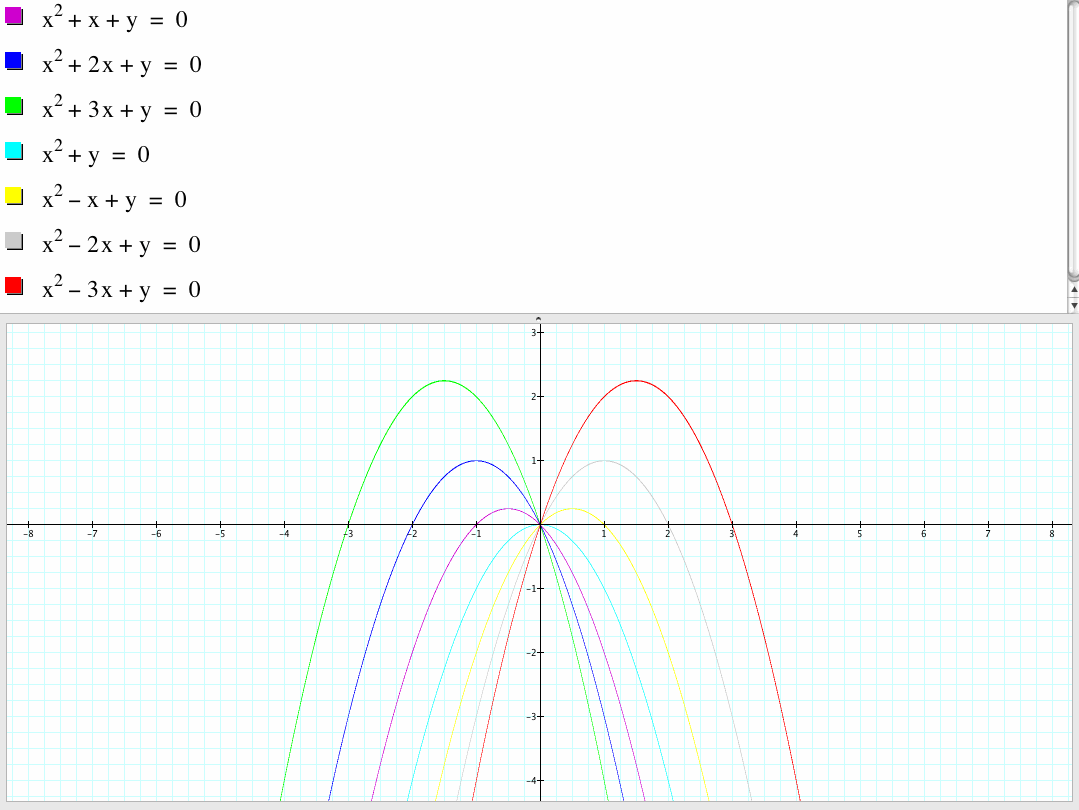
If we graph the family of parabolas is the xc plane, we observe that this family of graphs always pass through the origin point (0, 0) and they all open down.
Investigation 5.
Consider graphs in the xa plane
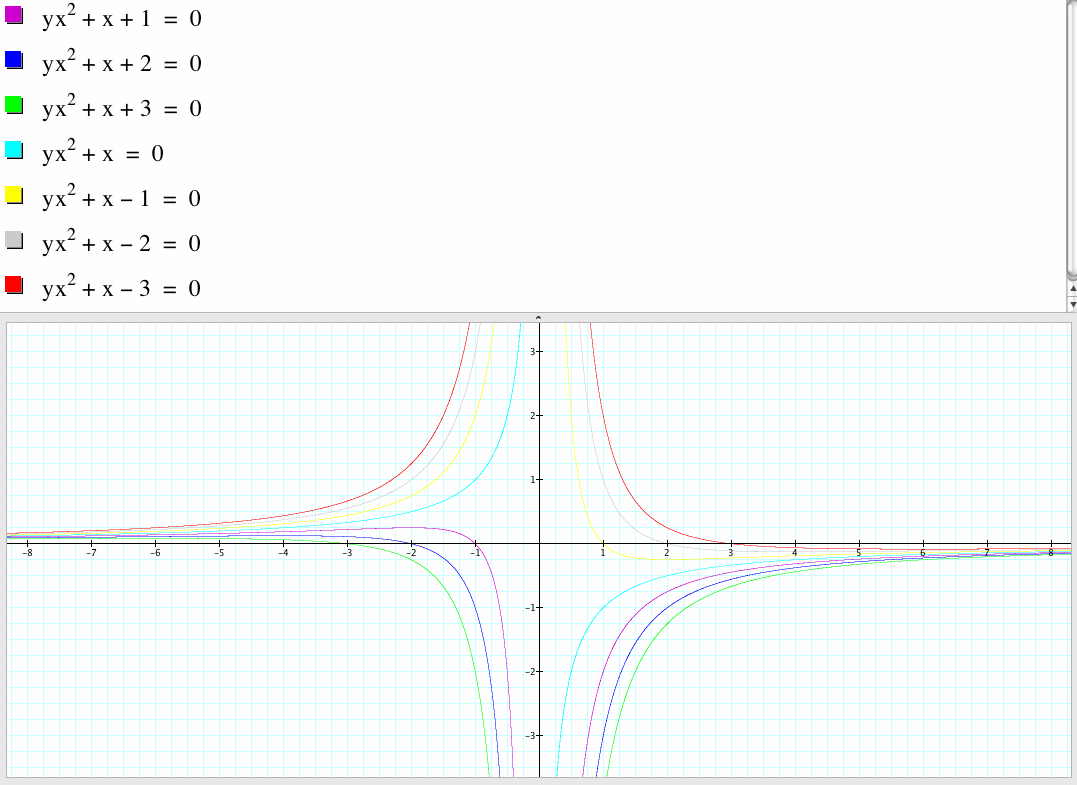
The above picture is the graphs in the xa plane. This family of graphs are hyperbolas. When c is positive, if x coordinate approaches 0, then the y coordinate will approach negative infinity. When c is negative, if x coordinate approaches 0, then the y coordinate will approach positive infinity. When c is 0, we get the light blue graph.
Investigation 6.
Consider the equation a x^3+b x^2+c x +d =0
Explore the pattern of roots in the xb, xc, or xd planes. (Okay, maybe look at the xa plane too!)
1. Explore the pattern of roots in the xb planes.
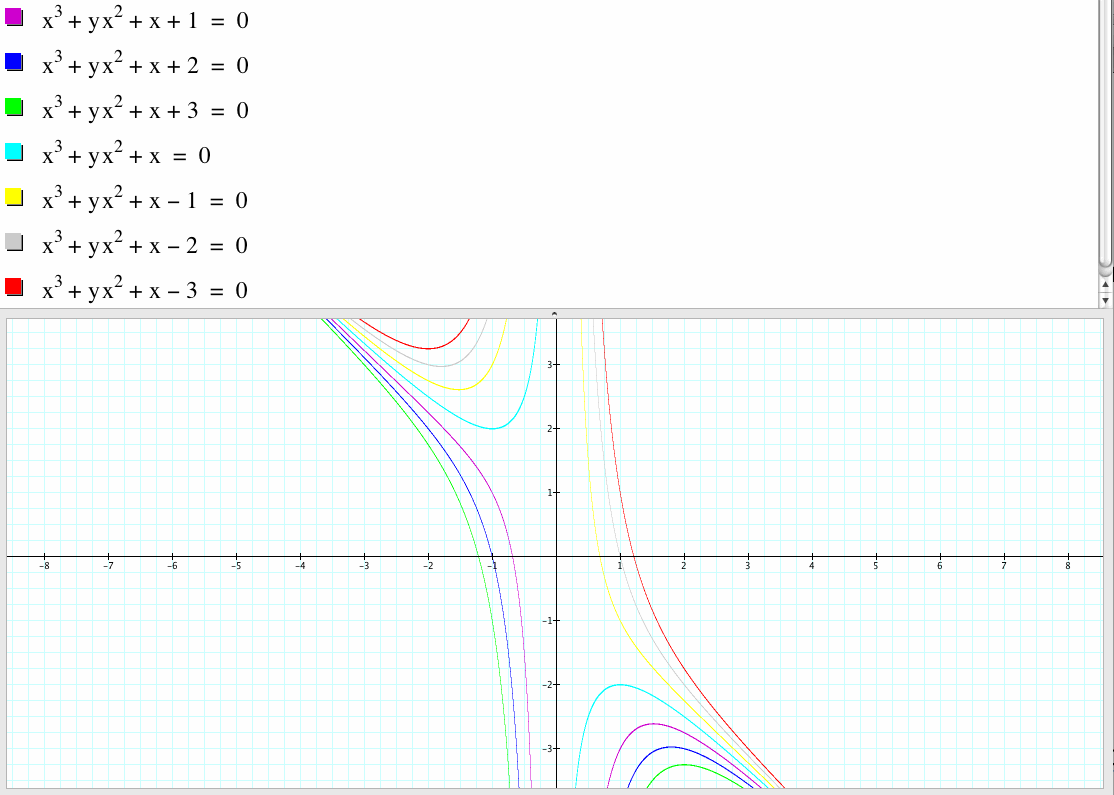
In the xb plane, if d is positive, then the equation always intersect the x-axis at two points and thus the equation has two roots. If d is negative, then the equation does not intersect the x-axis and thus the equation has no real roots. If d is 0, then we can factor out x, we get the green graph which is a hyperbola and the y-axis.
2. Explore the pattern of roots in the xc planes.
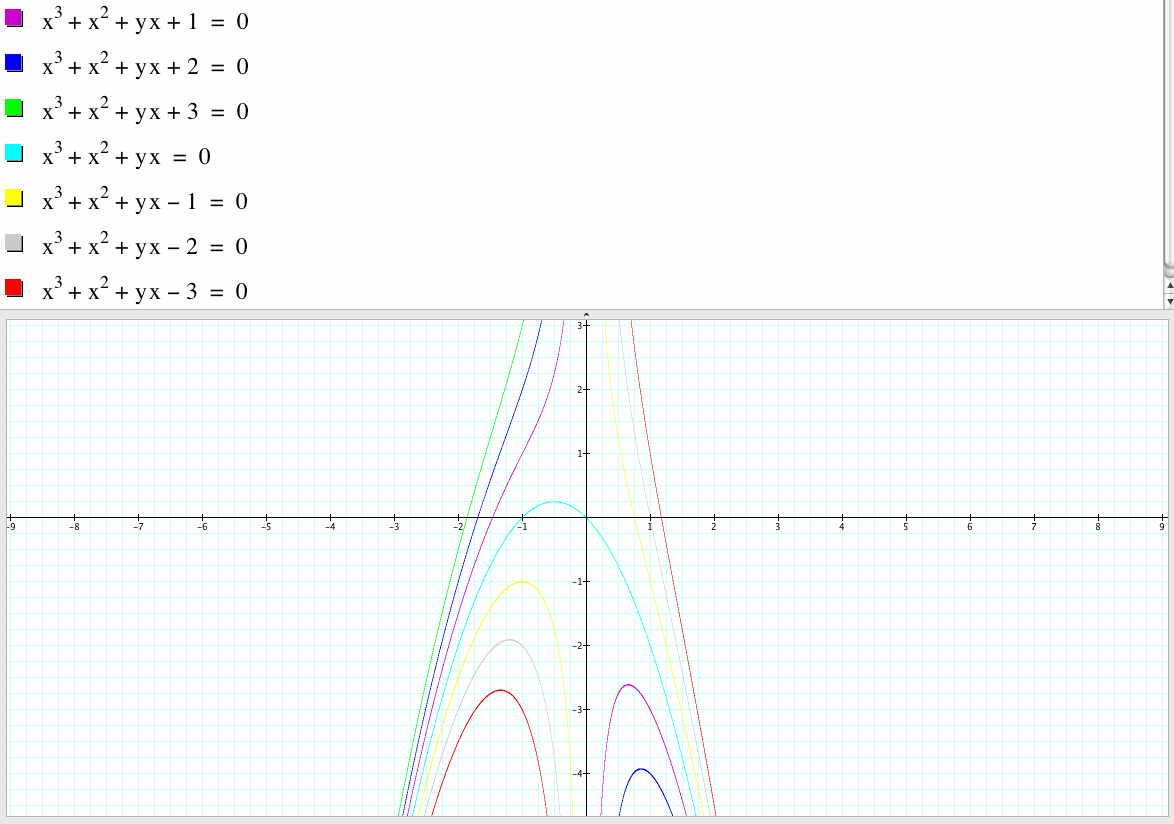
In the xc plane, if d is 0, then we can factor out x, we get the green graph which is a parabola and the y-axis. If c is positive, then the equation always intersect the x-axis at one point and thus the equation has one real root. If d is negative, then the equation also always intersect the x-axis at one point and thus the equation has one real root.
3. Explore the pattern of roots in the xd planes.
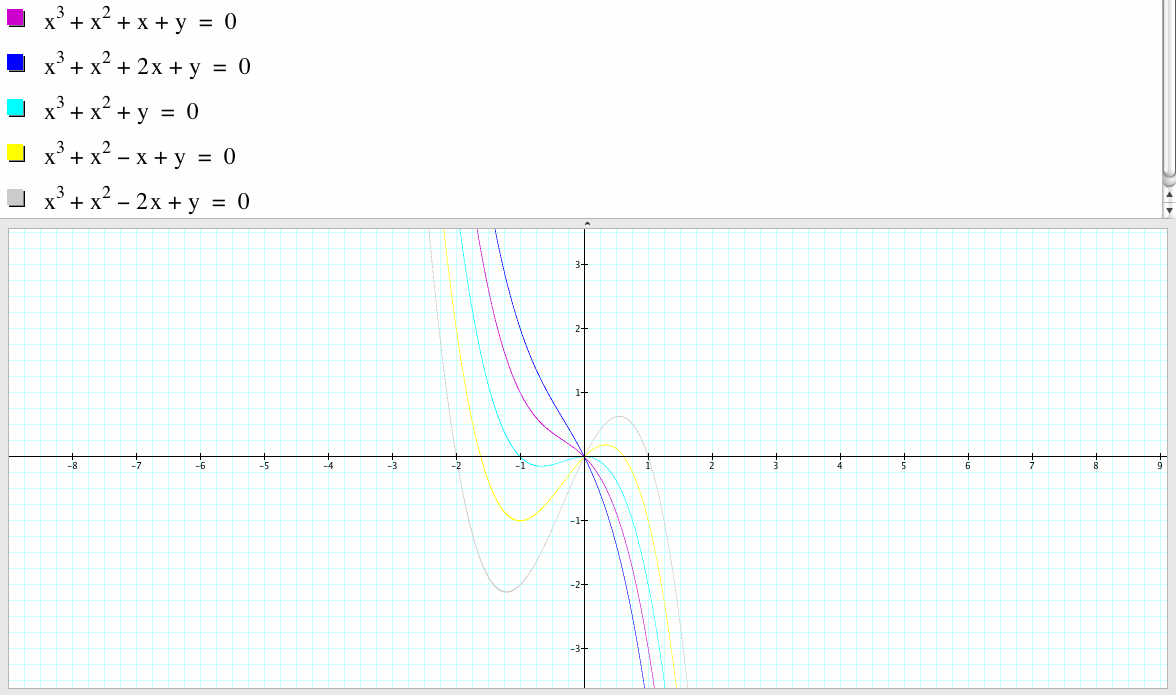
In the xd plane, if c is positive, then the equation always intersect the x-axis at one point the origin and thus the equation has one real root. If c is negative, then the graph intersect the x-axis at three points and thus the equation has three real roots. If c is 0, then the graph intersect the x-axis at two points and thus the equation has two real roots and the x-axis is tangent to the graph at the origin.
4. Explore the pattern of roots in the xa planes.
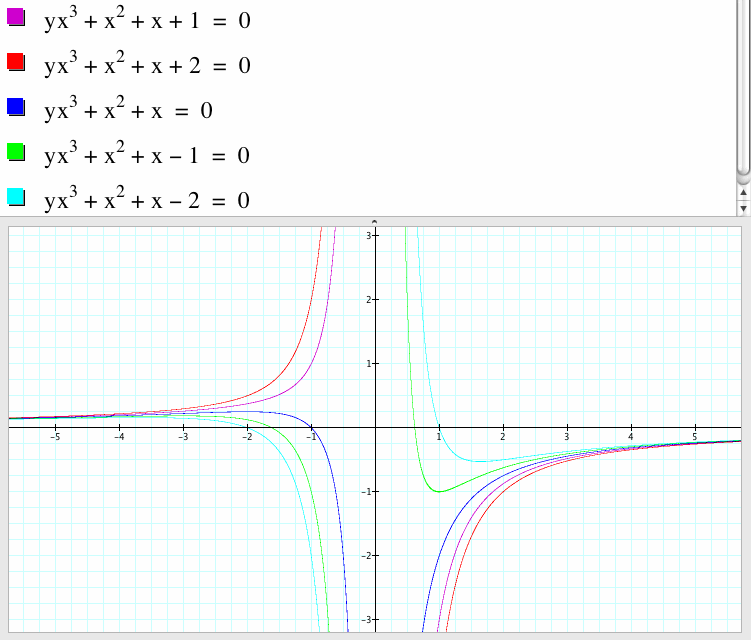
In the xa plane, if d is positive, then the equation does not intersect the x-axis and thus the equation has no real root. If c is negative, then the graph intersect the x-axis at two points and thus the equation has two real roots. If c is 0, then the graph intersect the x-axis at one point and thus the equation has one real root.