

Assignment 7:
Tangent Circles
by
Wenjing Li
Given two circles and a point on one of the circles. Construct a circle tangent to the two circles with one point of tangency being the designated point.
1. The two given circle one is inside the other and the tangent circle is inside the big given circle and outside the small given circle.
We know that the center of the circle that tangent to the two given circles will lie along a line from the center of the given circles with the specified point because the red circle is tangent to the the big green circle at the yellow point thus the line through the yellow point and the the center of the red circle will pass through the center of the big green circle. We want to find the center of the tangent circle. The segment from the center of the tangent circle to the center of the second given circle is the length of the sum of the radius of the tangent circle plus the radius of the given circle that did not have the given tangent point. We can find the same distance along the line through the given point from the center of the tangent circle by constructing another circle of the same radius with center at the given tangent point. We can construct an isosceles triangle that the center of the tangent circle is on the perpendicular bisector of the base of the isosceles triangle. The perpendicular bisector of the base of the isosceles triangle and the line through the yellow tangent point and the center of the big green circle intersect at a point which is the center of the tangent circle that we are looking for. Now we draw a circle with the center that we found and pass through the yellow given tangent point, then we will get a circle that tangent to the two given circles and pass the yellow given tangent point.

2. The two given circle one is inside the other and the tangent circle is inside the big given circle and the small given circle is inside the tangent circle.
To find the center of the tangent circle. The segment from the center of the tangent circle to the center of the second given circle is the length of the radius of the tangent circle minus the radius of the given circle that did not have the given tangent point. We can construct an isosceles triangle that the center of the tangent circle is on the perpendicular bisector of the base of the isosceles triangle. The perpendicular bisector of the base of the isosceles triangle and the line through the yellow tangent point and the center of the big green circle intersect at a point which is the center of the tangent circle that we are looking for. We draw a circle with the center that we found and pass through the given tangent point, then we will get a circle that tangent to the two given circles and pass the yellow given tangent point. Let us move the given tangent point along the given circle and trace the center of the tangent circle and we get an ellipse since the sum of the distance from the center of the tangent circle to the center of the two given circles is fixed.

If we put the two cases in one picture, we see that the trace of the blue tangent circle is the blue ellipse and the trace of the red tangent circle is the red ellipse.

3. The two given circle one is intersect the other. There are two tangent circles in this situation. One is the blue tangent circle is inside the big given circle and outside the small given circle. The other is that the red tangent circle is inside the big given circle and the small given circle is inside the red tangent circle. The trace the center of the blue tangent circle is an ellipse since the sum of the distance of the center of the blue tangent circle to the center of the two given circles is fixed. The trace the center of the red tangent circle is the red hyperbola.
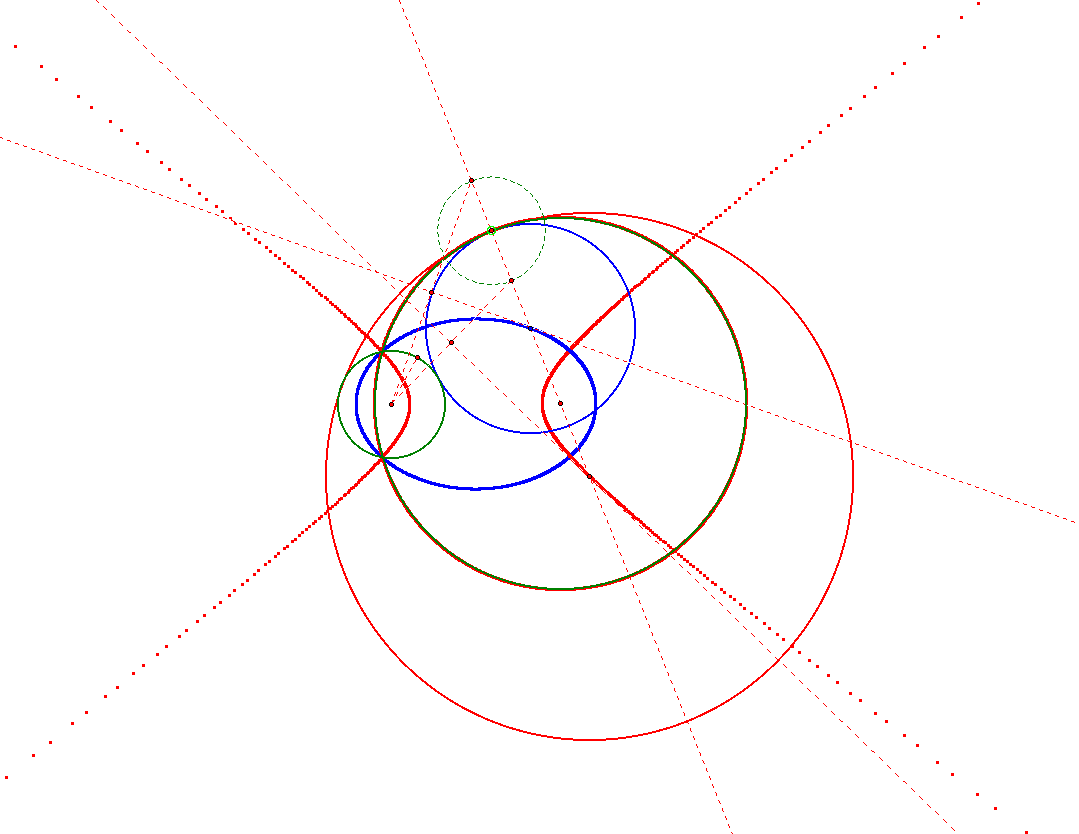
4. The two given circle are outside each other. We have two tangent circles in this situation. First situation is one given circle is inside the blue tangent circle and the other given circle is outside the blue tangent circle. The other situation is that the two given circles are both inside the red tangent circle. The trace the center of the blue tangent circle is the blue hyperbola. The trace the center of the red tangent circle is also a hyperbola the red hyperbola.

The red line in the picture is always tangent to the ellipse. We trace the line as the tangent point of the constructed circle moves around the large circle and we will get an envelope of lines all tangent to the ellipse.

