Assignment 8:
Altitudes and Orthocenters
by
Wenjing Li
1. Construct any triangle ABC.
2. Construct the Orthocenter H of triangle ABC.
3. Construct the Orthocenter of triangle HBC.
4. Construct the Orthocenter of triangle HAB.
5. Construct the Orthocenter of triangle HAC.
6. Construct the Circumscribes of triangles ABC, HBC, HAB, and HAC.
7. Conjectures? Proofs?
Does your construction look something like this?
What would happen if any vertex of the triangle ABC was move to where the orthocenter H is located? Where would H then be located? Click HERE for a GSP file with "move" buttons to see these animations? Explanation?
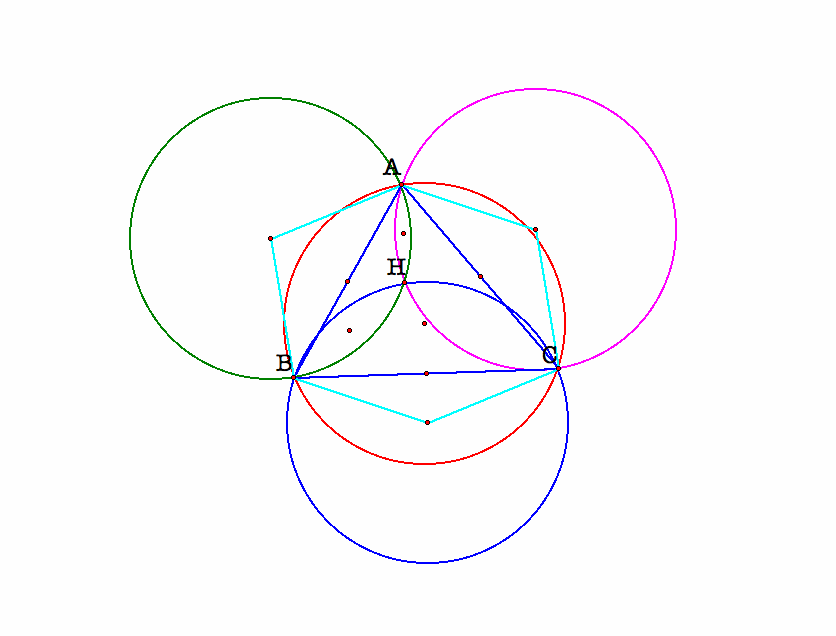
We investigate the orthocenters of triangle. Let's construct a triangle ABC. We draw three lines pass through the three vertexes A, B, C that perpendicular to the corresponding sides BC, AC AB and the intersection is the othocenter H of the triangle ABC. Then we construct three lines pass through the three vertexes H, A, B of the triangle HAB that perpendicular to the corresponding sides AB, HB, HA and the intersection is the othocenter H1 of the triangle HAB. Similarly, we construct three lines pass through the three vertexes H, B, C of the triangle HBC that perpendicular to the corresponding sides BC, HC, HB and the intersection is the othocenter H2 of the triangle HAB. We also construct three lines pass through the three vertexes H, A, C of the triangle HAC that perpendicular to the corresponding sides AC, HC, HA and the intersection is the othocenter H3 of the triangle HAC.
Now we construct three perpendicular lines pass through the midpoints of the segments AB, BC, CA and perpendicular to the sides AB, BC, CA respectively, the intersection point O is the center of the circumcircle of the triangle ABC. Then we construct a circle with center O and radius OA which is the red circle the circumcircle of the triangle ABC. Similarly, we construct three perpendicular lines pass through the midpoints of the segments AB, BH, HA and perpendicular to the sides AB, BH, HA respectively, the intersection point O1 is the center of the circumcircle of the triangle ABH. Then we construct a circle with center O1 and radius AO1 which is the green circle the circumcircle of the triangle ABH. Now we construct three perpendicular lines pass through the midpoints of the segments CB, BH, HC and perpendicular to the sides CB, BH, HC respectively, the intersection point O2 is the center of the circumcircle of the triangle CBH. Then we construct a circle with center O2 and radius BO2 which is the blue circle the circumcircle of the triangle CBH. And we construct three perpendicular lines pass through the midpoints of the segments AC, CH, HA and perpendicular to the sides AC, CH, HA respectively, the intersection point O3 is the center of the circumcircle of the triangle ACH. Then we construct a circle with center O3 and radius AO3 which is the purple circle the circumcircle of the triangle ACH. The following is our picture.
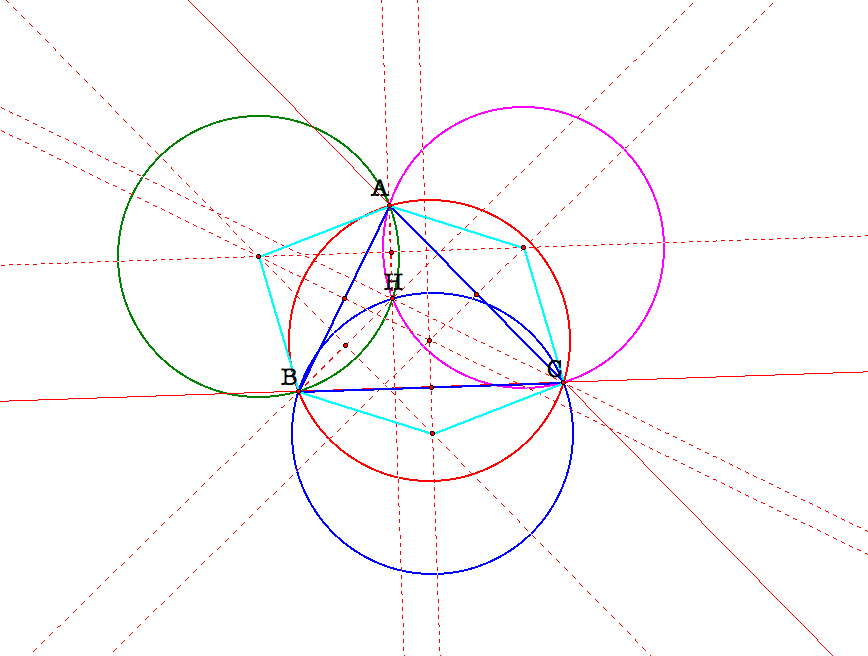
If we let all the perpendicular lines that we use in the construction shown, we have the following graph.
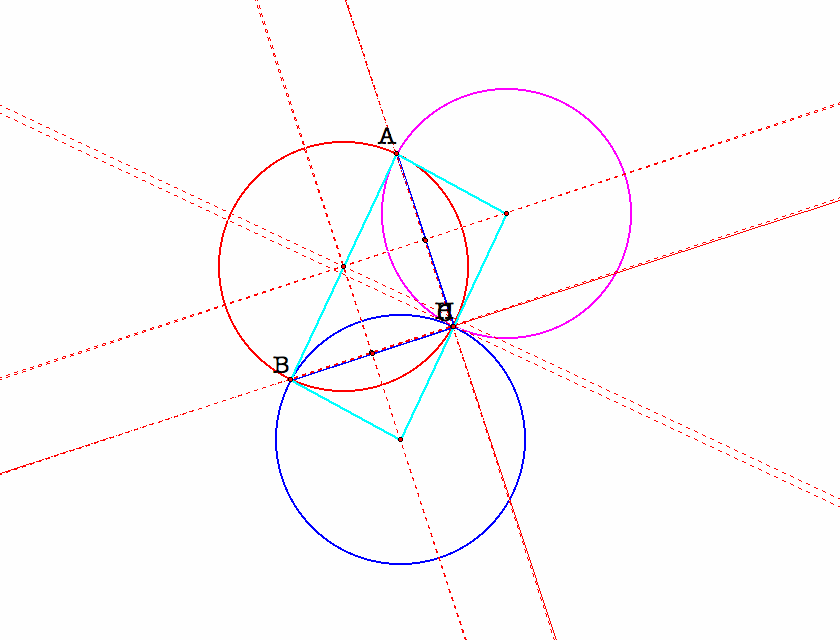
If we move the vertex A of the triangle ABC to where the orthocenter H is located, then the red circumcircle of the triangle ABC and the blue circumcircle of the triangle HBC will overlap. Then H will be located at the position of vertex A. Since we move the vertex A of the triangle ABC to the vertex H of the triangle HBC, thus the the red circumcircle of the triangle ABC will move to the blue circumcircle of the triangle HBC. The following is our graph of how H and A overlap and how the red circumcircle and the blue circumcircle overlap.
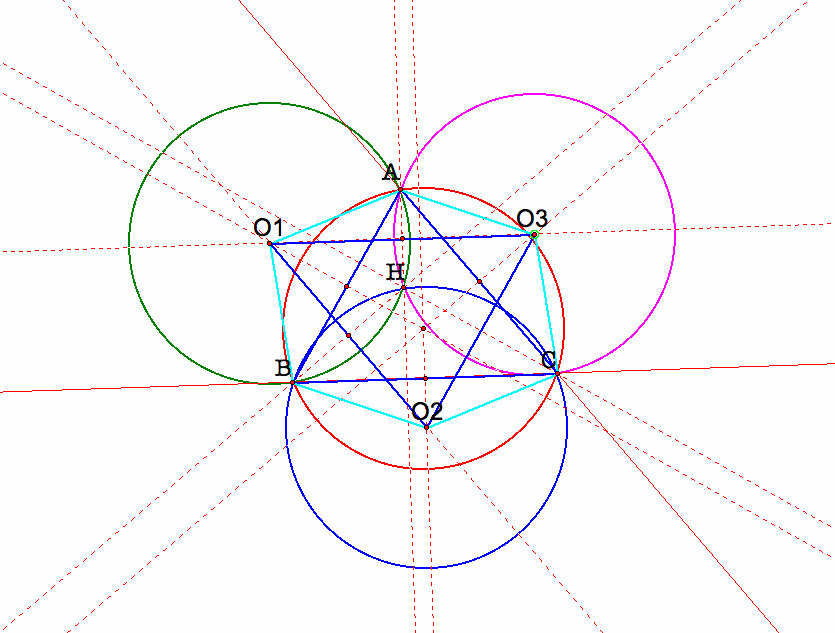
The four circmcircle have the same radius, so AO1, BO1, BO2, CO2, CO3, and AO3 are all have the same length. We observe that AO1 and CO2 are parallel, O1O2 is parallel to AC, therefore the length of O1O2 is the same as AC. Similarly, the length of AB and the length of O2O3 are the same, the length of BC and the length of O1O3 are the same. Hence we connect the center of the three outer circle and get a triangle O1O2O3 which is similar and congruent to the original triangle ABC.
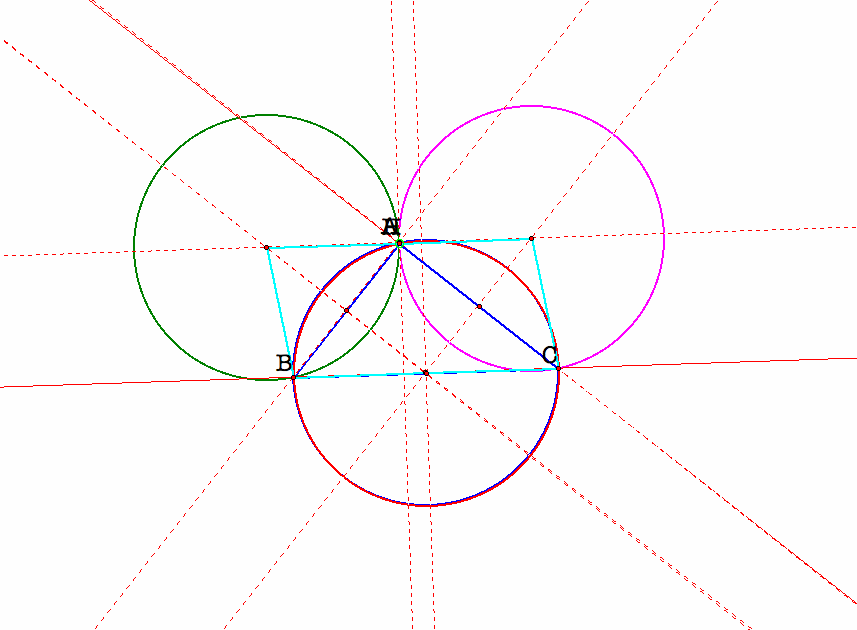
Let us move the vertex B of the triangle ABC to where the orthocenter H is located, then the red circumcircle of the triangle ABC and the purple circumcircle of the triangle HAC will overlap. Then H will be located at the position of vertex B. Since we move the vertex B of the triangle ABC to the vertex H of the triangle HAC, thus the the red circumcircle of the triangle ABC will move to the purple circumcircle of the triangle HAC. The following is our graph of how H and B overlap and how the red circumcircle and the purple circumcircle overlap.
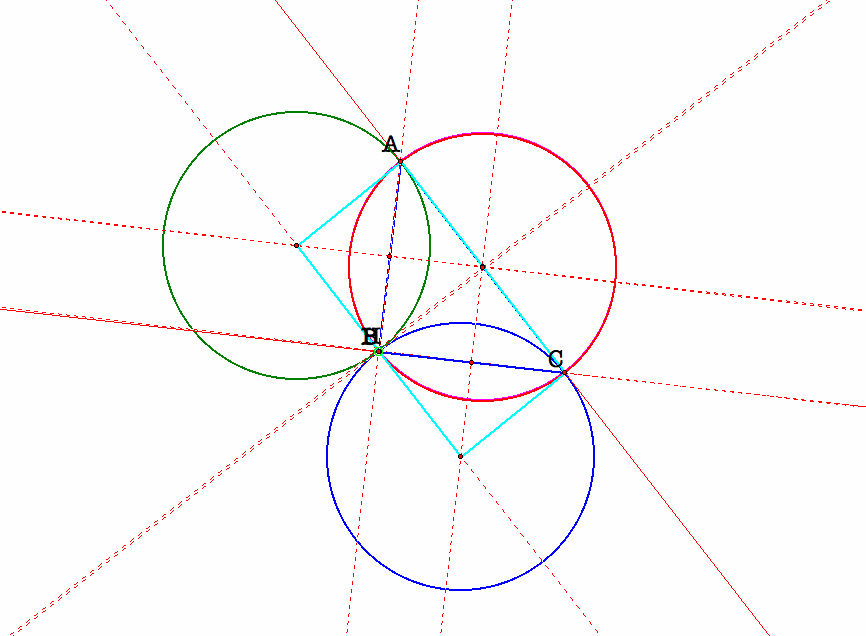
Now we move the vertex C of the triangle ABC to where the orthocenter H is located, then the red circumcircle of the triangle ABC and the blue circumcircle of the triangle HAB will overlap. Then H will be located at the position of vertex C. Since we move the vertex A of the triangle ABC to the vertex H of the triangle HAB, thus the the red circumcircle of the triangle ABC will move to the green circumcircle of the triangle HAB. The following is our graph of how H and C overlap and how the red circumcircle and the green circumcircle overlap.