In this investigation, we will look into polar equations in the form
with special attention on the parameter k.
Before we begin the investigation, as an introduction, let us view some random samples of this polar equation, to stir up some interest in the audience.
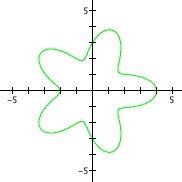
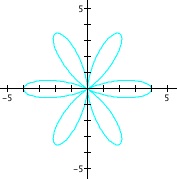
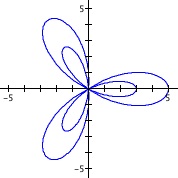
Some samples of our polar equation
Let us look at a simple case of polar equations, which is in the form
where b is a constant. Note that this is a particular case of our main polar equation, with a = 0 and k = 0. If we graph this polar equation, we get the following graphs:
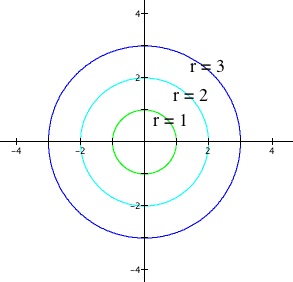
Polar equations of form r = b
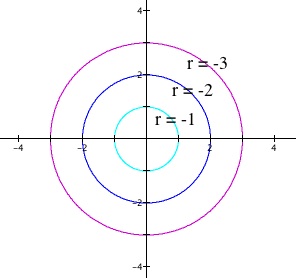
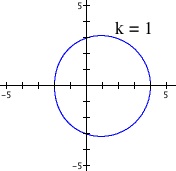
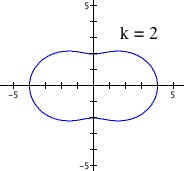
Clearly, the polar equation r = b is a circle with radius b. Why is this so?
In the polar equation, a point is defined by the central angle
and the distance r from the point to the center of origin.
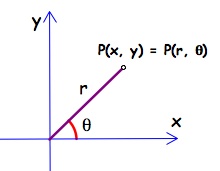
A point is defined by parameters r andin Polar form
The polar equation r = b means that for every value of central angle, the distance between the point and center of origin is always constant. Thus, it is the polar equation of the circle. Note that increasing the value of b will result in some kind of increase in the size of the graph in polar format.
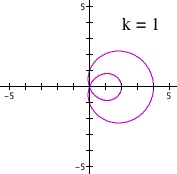
In the investigation of our polar equation 
, let us choose a simple case of a = 3, b = 3, and k = 1, and change each parameter to explore the effect of each parameter. The graph of our sample equation 
will be:
In the animation below, the parameter a is set from a = 0 to a = 8 in the polar equation 
.
Changing parameter a from a = 0 to a = 8
At a = 0, the graph is a circle center at the origin with radius 3. As the parameter 'a' increases from a = 0 to a = 3, a little dent begins to form in the left side of the circle, and the circle gets bigger while the center shifts to the right. As the parameter 'a' increases above a = 3, a loop begins to form in the middle of the circle, and this loop continues to increase, approaching the outer circle but never quite reaching it.
Now, let us examine the effect of parameter b in our sample polar equation . Let us explore using an animation that sets b from b = 0 to b = 8.
Changing parameter b from b = 0 to b =8
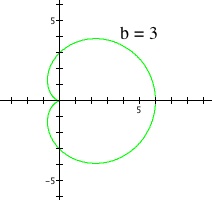
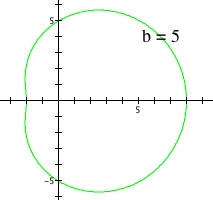
Snap shots of the above animation for certain values of b
At b = 0, the graph is a circle of diameter 3, with its two horizontal endpoints located at x = 0 and x = 3. As b increases from b = 0 to b = 3, we see that another circle separates from the original circle, and this inner loop becomes smaller until it disappears at b = 3. Then, as b increases above b = 3, the graph increases in size and approaches a perfect circle.
A careful review of the behaviours of paramters 'a' and 'b' from the sections above reveals an interesting relationship between them. Their patterns behave in an opposite manner as their values are increased to infinity. First, the parameter 'a' starts off as a perfect circle at a = 0, then a dent begins to occur in the side, which becomes a loop as 'a' increases above 'b', and then the inner loop begins to increase. As 'a' goes out to infinity, the inner loop aproaches to become one with the outer circle, but never becoming one, similar to the idea of an asymptote. On the other hand, the parameter 'b' starts out at b = 0 as the case of 'a' approaching infinity, and behaves in the opposite direction of parameter 'a'. For parameter 'b', the perfect circle at b = 0 separates into two circles, forming two circular loops, and the inner loop disappears when b = a, and then it approaches to become a perfect circle but never being able to do so.
In summary, the infinity case of parameter 'a' is the start off case of parameter 'b', and the infinity case of parameter 'b' is the start off case of parameter 'a'. The neutral case seems to be when a = b. So the shape of our original polar equation
depends on the relative size of 'a' and 'b', when k = 1. (When k = 1, this is the base case of our polar equation, which will become clear why in the next section.)
The relative size of parameters 'a' and 'b' determines the shape of the base graph, when k = 1. The following are the three cases:
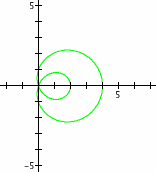
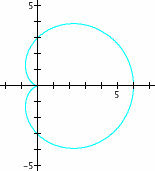
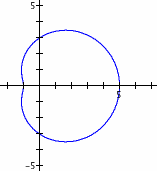
Left: a > b, Center: a = b, Right a < b
Finally, let us begin our investigation into the parameter 'k', which I name the "Great Divider." In general, the parameter k divides the graph into k equal sections of the base case, which is when k = 1 in the polar equation . Since the shape of the divided graph depends on the base case when k = 1, we will look at the effect of parameter 'k' for three cases: i) a = b, ii) a < b, iii) a > b.
i) When a = b
Remember that this is the neutral case between the two opposing effects of the parameters 'a' and 'b'. Setting k = 1 gives us the base case, which is the first graph in the figure below, and the equation I chose for the base case is . Dividing this base case into k sections results in the next four graphs in the figure. Note that all the divided parts within each graph are symmetric and are nicely shaped.
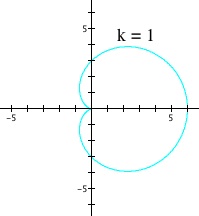
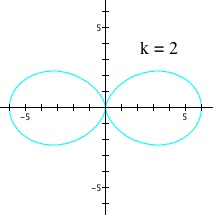
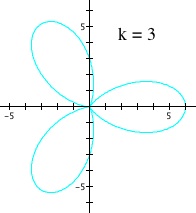
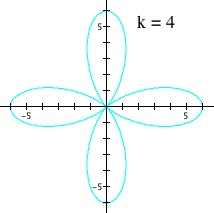
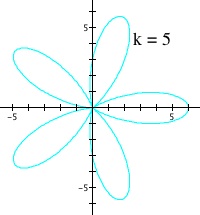
The effect of parameter k when a = b
ii) When a < b
Now we will explore how the parameter 'k' does it's cutting when a < b. The first graph in the figure below is our base case of k = 1, where I chose a = 1 and b = 3. The base graph is not a circle, but a dented one, as this is the general shape when a < b. Dividing this base graph for k > 1, we obtain the following graphs. We see that the divided parts do not reach the origin.
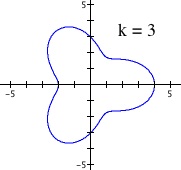
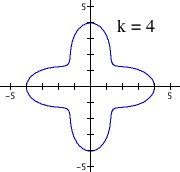
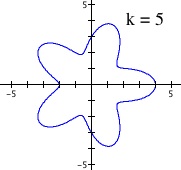
The effect of parameter k when a < b.
iii) When a > b
For a > b, the base graph of our polar equation will take the general form of the graph below.
General shape when a > b
So for this case, what will be the result of increasing paramter 'k'. How will dividing this graph with 'k' look like?
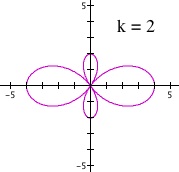
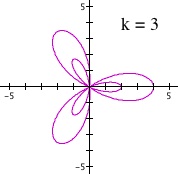
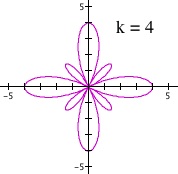
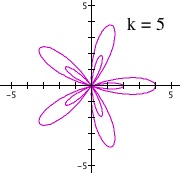
Effect of parameter k when a > b
We obtain a surprising result when dividing this case of a > b. For odd integers of k > 1, we see that the inner loop stays in the outer loop for each divided segments. However, for even integers of k, we see that the inner loop gets divided into separate segments than the outer loop.
The behavior of the polar equation is quite predictable for any set of integer values of a, b, and k. This polar equation can be easily controlled to generate different shapes of graphs. First, the base graph of k = 1 can be determined by the relative size of parameters 'a' and 'b'. Then, the parameter 'k' will divide it into k equal sections.
So can you figure out how to obtain the following graph?
A green sun...