

In this investigation, the focus will be on the use of spreadsheets in exploring mathematical relationships in real life situations. The use of spreadsheets enables one to see the relationship between certain variables and to explore new patterns. These relationships and patterns can greatly help guide one into developing mathematical formulas that are present in the situation. We will use spreadsheets to help us solve the problem of determining the maximum volume of a lidless box that is created by cutting squares on each corner of a rectangle. The spreadsheet will be used to let us see how the volume is affected by different amounts cut off on the sides. In the "Further Exploration," we will investigate the maximum volume of a lidless box for different dimensions of a rectangle that has a fixed area.
Suppose in a factory that manufactures cardboard boxes, lidless boxes are formed by cutting out squares from each corner of a rectangle cardboard with dimensions 8 x 5. In order to utilize the given rectangle most effectively, the factory needs to know what size squares should be cut off from each corner. What is the size of the squares being cut off that gives the maximum volume, and what is the maximum volume?

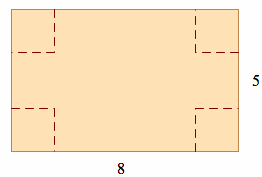

A lidless box formed by cutting out squares of same size from each corner
The aim here is to calculate the volume of such lidless boxes for the whole range of possible size of squares, and investigate how the volume is related to the size of such squares. Let us set up a diagram and label them. Let us denote x the side of the squares that are being cut off from each corner.


Setting up the diagram
From the figure above, we see that when we fold the flat carboard into a lidless box, the dimensions become width 8 - 2x, length 5 - 2x, and height x. Using the standard formula for volume, the volume V of the lidless box can be expressed as,
![]()
Now we can set up the spreadsheet using this volume formula. Let us set up a spreadsheet such that x ranges from x = 0.1 to x = 2.5 in increments of 0.1, and calculate the volume for these values of x. Note that x cannot be larger than 2.5, or else there will be no width left to construct the box. In the spreadsheet below, I have denoted 'w' as 5 - 2x and 'l' as 8 - 2x.

Table 1. Volume of lidless box for different values of x
Let us also graph this data, as this will help us see the relationship more clearly.

Graph 1. Volume of lidless box vs. x
The graph reveals that there is one point where the volume of the lidless box is maximum. The shape of the graph looks like a upside-down parabola, with the vertex being the maximum volume. From the graph we see that the maximum volume occurs when x is approximately 1.
Let us now look at the table now, concentrating on the highlighted section. In the table, the maximum volume of 18 occurs at x = 1. This seems to be our answer. However, with some careful thought, we should be cautious with this answer. Because we have used increments of 0.1, the maximum volume may occur at some point close to x = 1.
Now that we have observed the pattern, let us use mathematics guided by this use of spreadsheets to determine the point of maximum volume.
In this mathematical analysis, the maximum volume will be determined using Calculus. It is likely that other approaches lead to the same answer, however, I found it difficult to do so. (I could not apply the three dimensional Arithmetic Mean - Geometric Mean to this problem.)
Using the Volume equation from above, the volume V of the lidless box that is formed by cutting squares of side x is,
![]()
Expanding the equation and simplifying gives,
![]()
Now let us take the first derivative of V against x.
![]()
Setting the first derivative equal to zero and solving for the roots will give the critical points.

As the domain under our consideration is 0 < x < 2.5, the critical point we seek is x = 1. From the shape of the graph, we know that this critical point is a local maximum point.
Therefore, the maximum volume indeed occurred at x = 1, and gave the maximum volume V =18.
In our first investigation, the lidless box was constructed from a 5 x 8 cardboard by cutting out squares of sides 1, and the maximum volume of such a construction was found. What if the original rectangle is of a different dimension but same area? Will they have different maximum volumes of lidless boxes? If they all have different maximum volumes, then what dimension of length and width will give the highest maximum volume? In this Further Investigation, we will explore the maximum volume of a lidless box for different dimensions of rectangles that have the same area, and find the dimension that gives the highest among the maximum volumes.
Let us fix the area of the intial carboard box at 40. This area is equal to the area we had in our first investigation. The approach that we will take involves choosing the width and the length of the cardboard so that it has a fixed area of 40, calculate the size of the squares that are cut off that will give the maximum volume of that particular dimension, and then compare the maximum volume for each selected dimensions.
First, let us label the diagram as follows: the length as m, the width as n, and the sides of the squares being cutt off as x. And also, let us walk through the mathematical process that sets up the equations to calculate the volume and the 'x' value that gives the maximum volume.

Setting up the diagram
For a dimension of m x n, the volume is
![]()
Expanding and simplifying this equation gives,

Taking the first derivative,
![]()
The critical points occur where the first derivative equals to zero. Using the quadratic formula for the roots,

We have two roots which are two critical points of our volume equation. Hence, we need to determine which one of these roots lie in our domain. One of them will lie in our domain of 0 < x < min(m/2, n/2). We could use the logic function in the spreadsheet program to choose the root that lies in the domain, and use this root to calculate the maximum volume.

In the table below, I have set up m and n such that their product is 40. The x1 and x2 columns are the two roots of the first derivative function which are the critical points. These roots were calculated using the equations right above us. The final column is the value of maximum volume for that particular dimension of m x n.
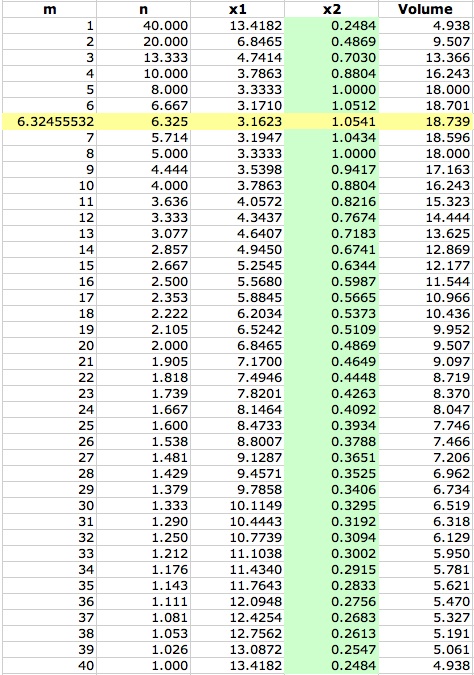
Table 2. Maximum volume for different dimensions of m x n.
After the x1 and x2 roots were calculated from the spreadsheet, I noticed that x1 was always larger than x2, and more importantly, the x2 column always lied in our desired domain. So there was no need for any use of logic functions. The x2 values are the sides of the squares that give the maximum volume for that particular dimension of m x n.
* Note the yellow highlighted row. I have inserted the case when m = n in the table, because this dimension is a special case of a square.
Let us take a look at the graph, as it is easier to see the relationship.

Graph 2. Maximum volume V vs. length m
The graph shows that there is exactly one case that gives the maximum volume, and the maximum volume decreases as other dimensions are used. According to the table and graph, the maximum volume happens when m = n, that is when the dimension of cardboard is a perfect square. This is in accordance with our expectations, as usually the solution to these maximum questions occurs when the dimension is a square.
Therefore, if the dimensions of cardboard is varied, the maximum volume of the lidless box that can be constructed from that dimension also varies. Also, the dimension that gives the highest maximum volume is when the rectangle is a square. The dimension 5 x 8 used in the first investigation produces a maximum volume of 18, which is a slight drop off from the highest possible maximum volume. The 5 x 8 cardboard is a good dimension to use, as it is a nice multiple of integers.
The problem posed in the Further Exploration, was quite difficult for me to be proved mathematically. There is probably a way that this can be proved mathematically, however, it seems very difficult in my eyes. The use of spreadsheet was very effective in calculating the maximum volume for each case of dimensions, and also in comparing the different maximum volumes for different dimensions.