

A few years ago, the rules in college football was changed so that the the uprights were made 5 feet less than previously. Many commentators have railed about how much harder it is to kick a field goal from the harsh marks. The important matter is to figure out how this will change strategies in taking a field goal.
Suppose that the coach of the UGA's football team came to you, a math specialist, to obtain advice on this matter. If a field goal is being attempted from the harsh marks, at what yard marker does the kicker have maximum angle? Does taking a penalty in some circumstances give the kicker a better angle at the field goal? What else would you recommend?
Before we can set up a diagram to investigate the problem, we need to know about the dimensions of a football field. The following figure gives the dimensions according to the official NCAA/College Football rules.
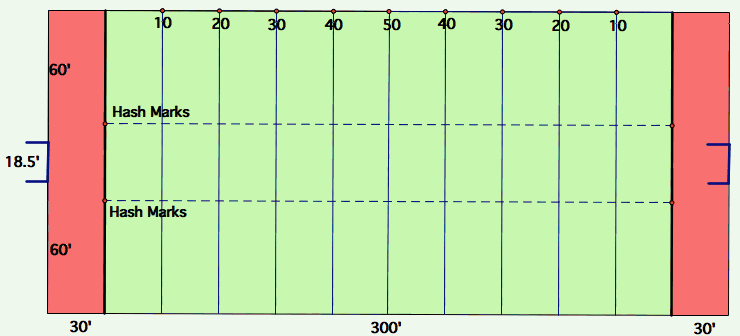
According to the NCAA/College football rules,
- The overall dimension: The length is 360 feet including the two end zones, and the width is 100 feet. (360' x 100' or 120 yards x 53 1/3 yards)
- End zones: 10 yard deep.
- Hash Marks: The hash marks are 40 feet wide and start 60 feet from the sidelines.
- Goal Posts: The goal posts measure 18 feet 6 inches wide. (or 18.5 feet)
Let us use Geometric Sketch Pad (GSP) for this investigation. I have constructed a model with the same ratio of dimensions as the official dimensions of NCAA.
Click HERE to download the model for investigation.
Let us measure the angle at various distances (in yards) along the top hash line.
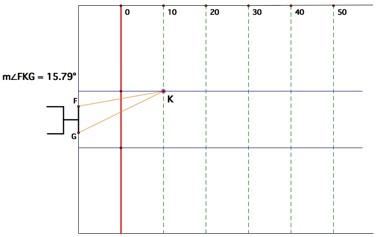
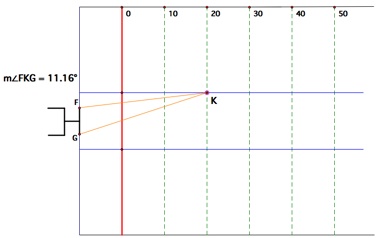
The angle of kick for a field goal at 10 yards and 20 yards
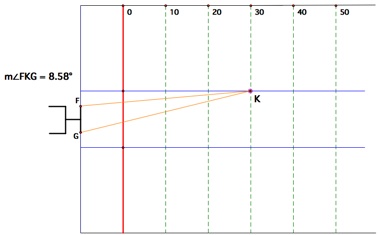
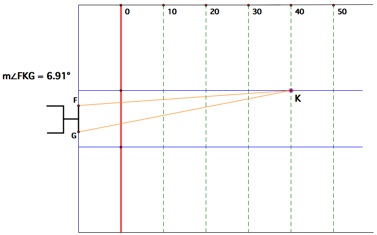
The angle of kick for a field goal at 30 yards and 40 yards
The angle measurements at various distances clearly shows that the kicker has a wider range of angle to make a field goal when he is closer to the upright. (This is within the allowance of a field goal range) We can conclude that the kicker has a "better angle" in terms of the width of angles from a closer distance.
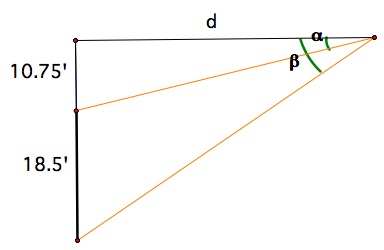
Since it will be boring to finish the investigation here, let us construct a mathematical equation that gives the angle for field goal at various distances from the upright. If we let d be the distance from the upright (not from the 0 yard line) in feets (not in yards), then we can calculate the angle of field goal with the following diagram.
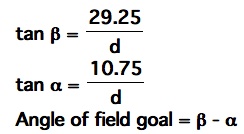
I have created an excel sheet for d' = 0 to d' = 48 yards (remember d is from the upright, not the 0 yard line), and created the following graph.
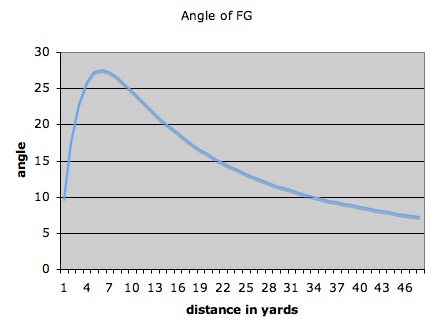
The graph clearly shows that in the possible field goal range, you get less of an angle further out from the upright.
Now let us calculate where the maximum angle occurs using Calculus. Yeah! . . ... By looking at the graph, the maximum angle occurs around d = 6 yards. Let us set up an equation in terms of y = angle of field goal in degrees, and d = distance from the upright in feet.
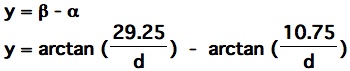
To find the point of maximum, we are going to take the first derivative of this equation and let it equal to zero. Recall that the derivative of f(x) = arctan x is given by f '(x) = 1 / (1 + x^2). Please Note that I have replaced the variable d with x to make the equations less confusing.
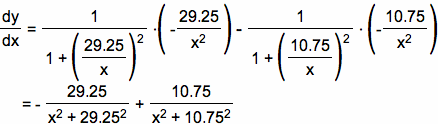
![]()
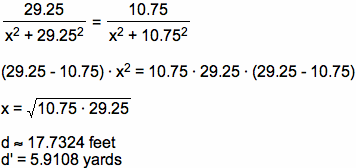
Therefore, the maximum angle occurs at approximately 6 yards or 18 feet from the upright.
*** NOTE: We can note an interesting pattern from the solution above. The maximum angle occurs at a distance of the square root of the two heights of the triangles. By going through the same steps, we can generalize the above solution so that the maximum angle happens at a distance of the square root of the two heights of the triangles.
Some commentators suggest to take a penalty and move back the field goal in order to obtain a "better angle" if the field goal is on the hash mark. (or near the hash mark). We have already shown that this is false if "better angle" is meant to be the width of the available angle. However, a kicker might also worry about another angle when taking a field goal kick. The farther the field goal is from the upright, the kicker may feel more comfortable because he is facing the upright in a more straight manner. That is, the kicker may also be concerned about the angle alpha in the figure below.

Now, one can explore how much more "straight" toward the upright does the field goal becomes for various distances.