

In this exploration, we will look into the tangency of lines and circles, and the special properties that are involved with them. If a line is tangent to a circle, then that means the line touches the circle at exactly one point. A circle can be tangent to another circle, which means that those two circles touches at exactly one point.
What are the possibilities of the intersection of a line and a circle? As shown in the figure below, a line can touch a circle at one point, two points, or none. We say that a line is tangent to a circle, if the line touches the circle at exactly one point.
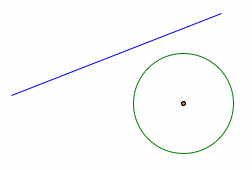
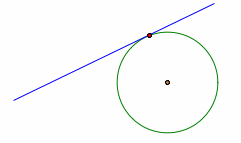
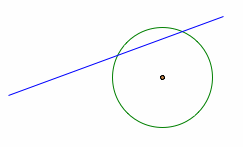
Different possibilities of intersection of line and circle
There is a special property when the line is tangent to a circle. In this case, the radius from the center of the circle to the tangent point is perpendicular to the tangent line.
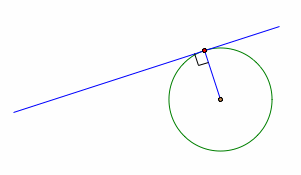
Property of tangent line and radius of a circle
How can two circles intersect with one another? Similar to the first case of a line and a circle, two circles can intersect one another in one point, two points, or none.
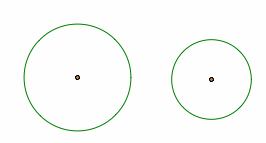
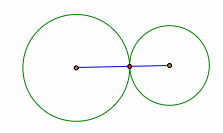
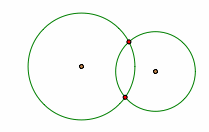
Different possibilities of intersection of two circles
When two circles touches one another at exactly one point, then we say that the two circles are tangent to one another. In this case, the two circles share a common tangent line at the tangent point.
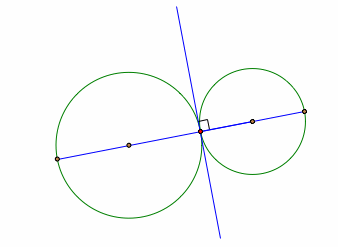
Common tangent line of two tangent circles
A special property can be noted when the two circles are tangent to each other: As this common tangent line is perpendicular to both radii of each circle at that point, it follows that the two radii and the tangent point lie along the same line.
Also, the two circles can be tangent in a different way. In this different arrangement also, the two circles share the same point of tangency and line of tangency at that point, which implies that the tangent point and the two centers lie along the same line.
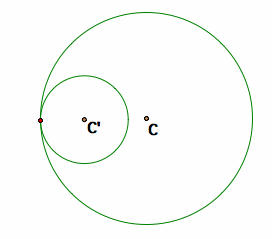
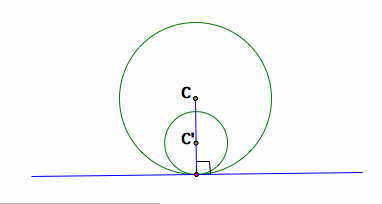
Two circles are tangent in a different way; Three points C, C', and Tangent point lie along same line
Given a line and a circle, we can construct a circle so that the circle is tangent to BOTH the given circle and the given line. For example,
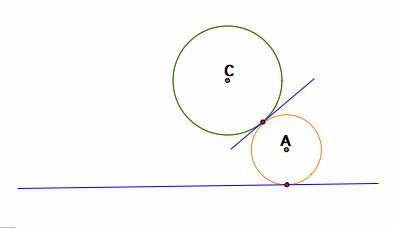
The circle A (orange) is tangent to both the given circle C and the given line
Also, the circle can be tangent to both the given circle and the line in a different way (bottom left figure). As explained from the above sections of tangency, the radius of the newly constructed circle (orange color) meets perpendicularly the given line, and also the newly constructed circle will have its center, the tangent point between the two circles, and the center of the given circle lie along a straight line. The relationships within this case is shown in the bottom right figure.
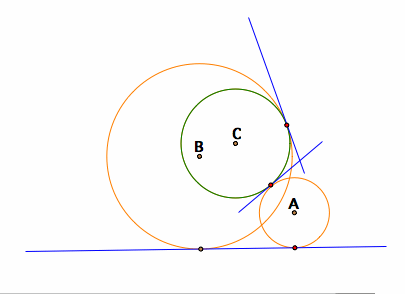
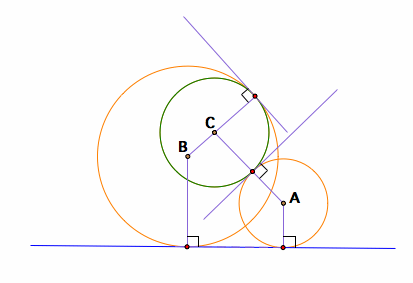
Another circle centered at B is also tangent to the given circle C and the given line
Now, our main question is how do we locate the center of such a circle that is tangent both to a given line and an given circle, and construct such a circle. We need to use some geometry to figure out the location of the center of this desired circle. We can use geometric relationships that will give us the exact location of the circle that will be tangent to both a given line and the given circle.
Let us choose a point P on the given circle that we want the newly constructed circle tangent at. Let us draw in the imaginary circle that will give the desired conditions, then try to look for a relationship that will give the location of point A. Remember that the radius from point A to the tangent line is perpendicular and that the points C, P, and A lie along a straight line.
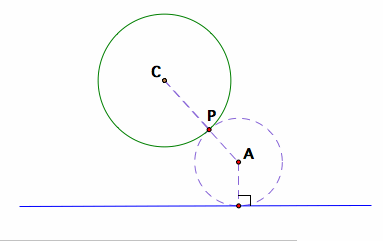
We see that the radius of circle A are the same length, and this looks like a good condition to use to find the location of point A. If we construct a line of tangency from point P, then we can construct two congruent triangles of APQ and ARQ.
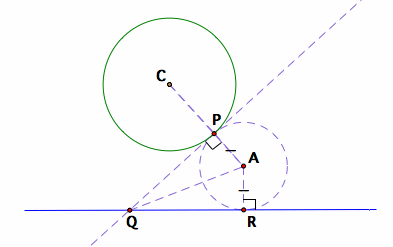
The two triangles APQ and ARQ are congruent, because AP = AR (radius of same circle), line AQ is common, and angle APQ = angle ARQ = 90 degrees.
Thus, if we use the relationships of PQ = QR, and of the line AQ being the bisector of angle PQR, then we can locate the point A. The center point A of the circle we wish to create, will lie along the intersection of ray CP and ray AQ.
** However, this construction does not work properly with GSP, because we lose the tangent line at point P when the point P moves to the other side of the circle. For this method of constructing the circle A to work, it will need three different cases that depends on where point P is located. In conclusion, do not use this method!! (I wasted a signficant amount of time doing this way T T)
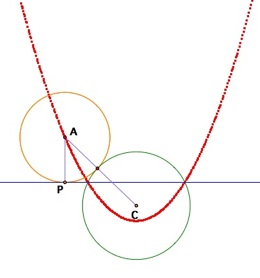
This time, let us choose a point P on the given line and try to locate the center of a circle that will be tangent both to the given line at that chosen point and also to the given circle. Let us draw in the circle that will have such properties, in order to explore some relationship that will give the center of the circle we wish to create.
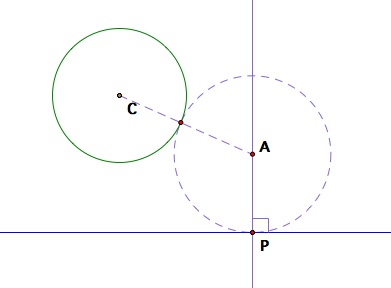
How do we locate the center A?
Remember that our goal is to find center A that is tangent to both the given circle and line, and note that we cannot find center A directly because we do not yet know the size of the radius AP. From the diagram above, we do know that the point A must lie along the the perpendicular from point P , if the circle is to be tangent at point P to the line.
In this approach, an equal length of the radius of the given circle C will be added to the other side of point P, so that an isosceles triangle can be formed, and then point A can be located from the height of that isosceles triangle. That is, if the radius r of the given circle is added at point P towards the bottom,
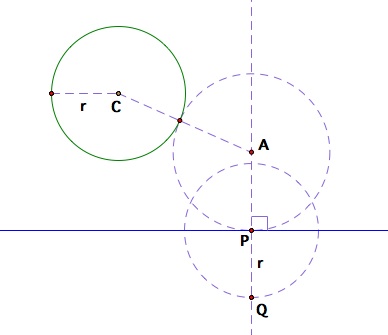
Adding a segment of length r at point P
Then we can create an isosceles triangle of ACQ. The height of this isosceles triangle from the mid point of segment CQ will intersect with the perpendicular ray at point P, thus giving our desired center point A. (Remember that we do not yet know the angle or location of segment CA.)

Special isosceles triangle ACQ
1. Given a line and a circle with radius r, choose an arbitrary point P on the line. Then, draw a perpendicular ray through point P.
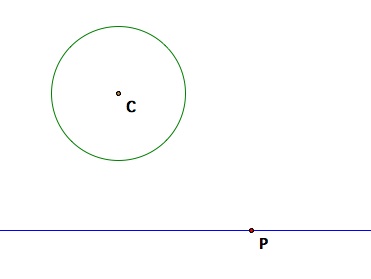
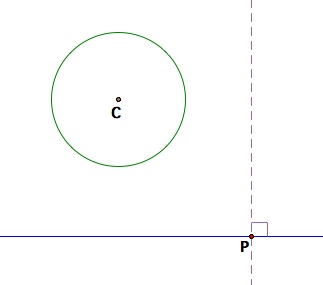
Step #1
2. From point P toward the bottom side of the perpendicular ray, obtain a point Q such that segment PQ = radius of given circle r. (An easy way to accomplish this is to draw a circle center at point P with radius r.)
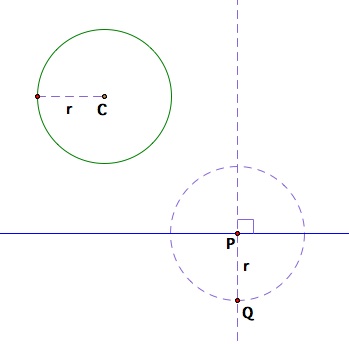
Step #2
3. Connect point C and point Q, which will be our base of the special isosceles triangle. Then locate the mid point of CQ and shoot a perpendicular ray through that midpoint.
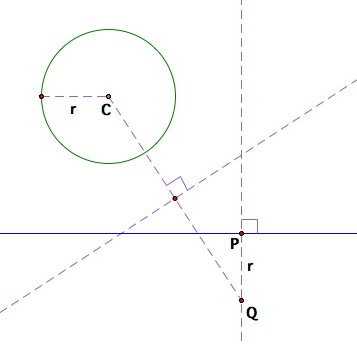
Step #3
4. The intersection point between the perpendicular from the midpoint of CQ and the perpedicular from point P gives the center of the circle we wish to create. We are done!
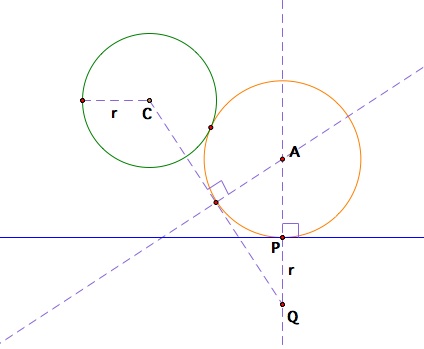
Step #4
*** Similarly, we can construct the circle that encompasses the given circle and is tangent to both the given circle and the line.
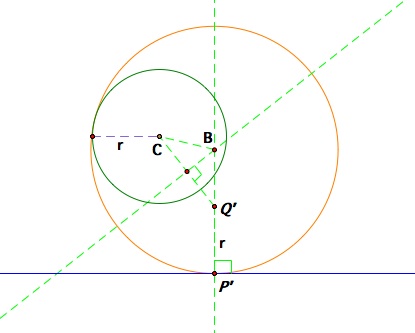
How to find the center of other case of tangent circle
In this exploration, we will investigate the locus of the centers of the circles we created from the previous sections. Let us construct both cases of circles that are tangent to a given circle and a given line, trace the locus of the centers of those circles.
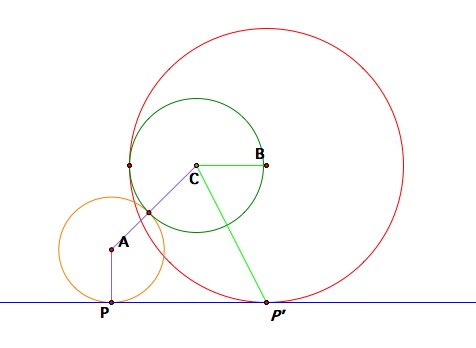
Given circle centered at C and given blue line; the tangent circles are centered at A and B
First, let us trace of the center point of the orange circle, which is the left figure, and then trace the center point of the red circle.
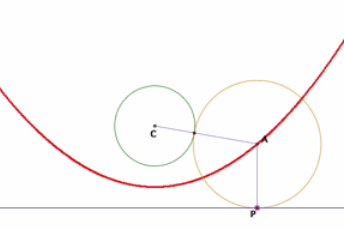
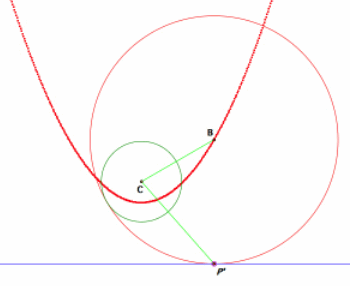
The locus of center point A (left) and B (right): Smile~
In both cases, we get a parabola. This can be proved geometrically by constructing a line parallel to the given line, which will be length r away either to the top or the bottom of the line. For the orange circle, constructing a parallel line such as in the diagram below show that the point B is always equidistance from point C and the newly constructed parallel line.
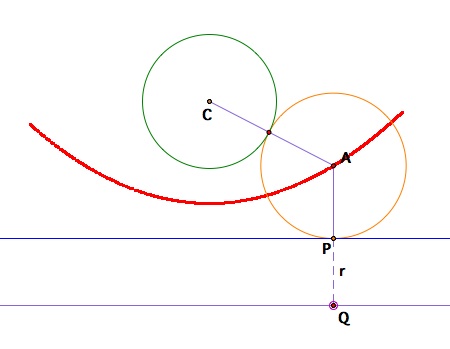
Point A is equidistance from center of given circle and newly constructed parallel line
Until now the given circle and the given line was separated and did not touch each other. Now, let us investigate when the given circle and the given line intersects at two points.
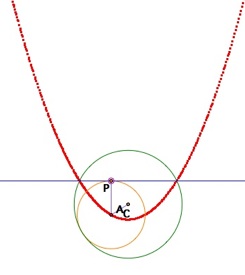
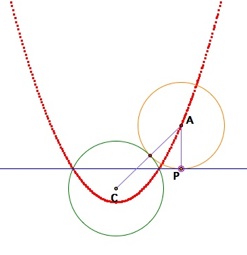
Case 1 of when given circle and given line intersect
Recall that we had another case of a circle that could be tangent to both the given circle and the given line. If we trace the locus of that red circle in the same given circle and intersecting line, then we get the following diagram. (The Case 1 and Case 2 could be and possibly should be drawn together in the same diagram.)
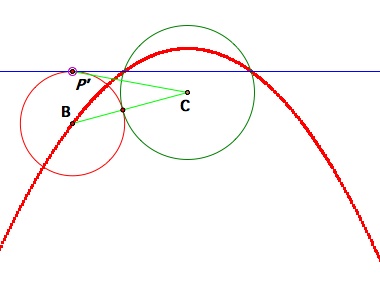
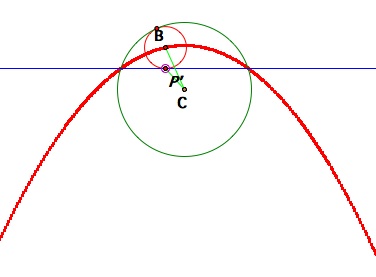
Case 2 of when given circle and given line intersect
Therefore, we can conclude that when the given circle and the given line intersect, the locus of the center of a circle tangent to both the given circle and given line will be two parabolas, each facing the opposite direction.
And for the last investigation, the given circle and given line can be tangent to one another. In this case, tracing the locus of the center of a circle tangent to both the given circle and given line gives a straight line perpendicular to the given line (a degenerate parabola) and a parabola.
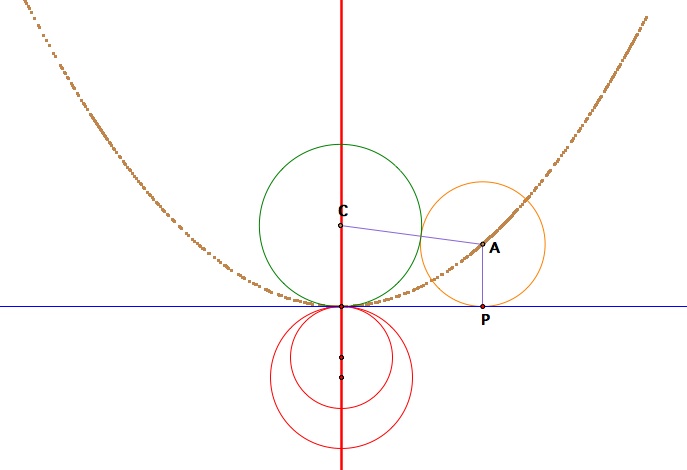
When the given circle and given line are tangent