

The Central Angle Theorem is very useful in solving questions that deals with angles within circles. The use of this theorem often simplifies a complicated situation into a rather simple one. The Central Angle Theorem is 'central' to many geometric questions involving circles in EMAT 6600, and is highly recommended (by me ^ ^;) to be looked into.
The Central Angle Theorem states that the central angle from two chosen points A and B on the circle is always twice the inscribed angle from those two points. The inscribed angle can be defined by any point along the outer arc AB and the two points A and B.
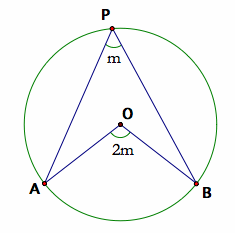
The Central Angle Theorem
Note: The Central Angle Theorem says the inscribed angle APB can have the point P anywhere along the outer arc AB, and the angle relationship will still hold.

All inscribed angles of same arc AB are equal in size
For those who would like to test that whether this is really true, you can test the Central Angle Theorem with this GSP file: CLICK HERE. (The file measures the inscribed angle and central angle for any position of points P, A, and B.)
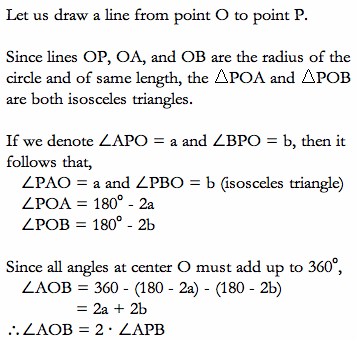 |
|
The following exercise utilizes the Central Angle Theorem and is a good example to get a feel for this theorem.
Problem #13: The internal angle bisectors of triangle ABC are extended to meet the circumcircle at points L, M, and N, respectively. Find the angles of triangle LMN in terms of the angles A, B, and C. Does your result hold only for acute triangles?
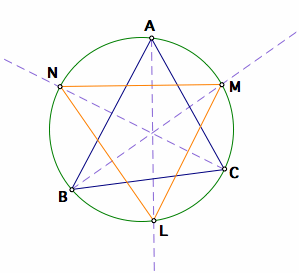
Problem #13
Solution:
Since each angle A, B, and C are bisected with extended lines, let us label each bisected angle with a, b, and c.
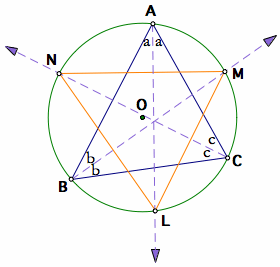
Labeling each bisected angle
Let us look at Arc BL in the bottom-left diagram. By the Central Angle Theorem, the inscribed angle BAL is equal to the inscribed angle BML. This is because those two inscribed angles share the same two base points B and L along the arc. Similarly, from the base arc CL in the right diagram, angle LAC = angle LNC.
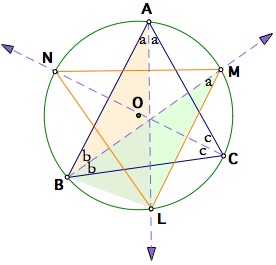
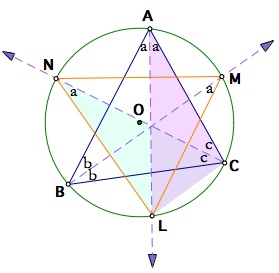
Base arc BL in the left & Base arc CL in the right
If we continue the same process for arcs AM, MC, AN, and NB, then we will have the following angle relationship.
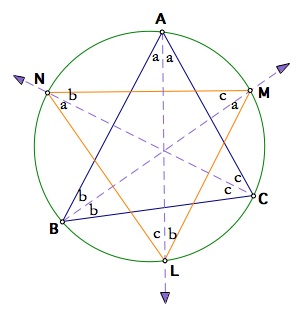
Applying Central Angle Theorem for arcs AM, MC, AN, and NB
Now, we can express the three angles L, M, and N in terms of A, B, and C.
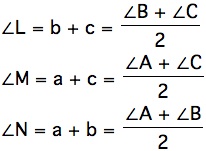
End of Solution!
*** The solution did not depend on whether the triangle was acute or obtuse. The same angle relationship will hold for an obtuse triangle also.