

In the following investigation, the definition of a pedal triangle and a pedal point will be introduced. The pedal triangle is associated with a pedal point which can be located anywhere along the plane. We will explore when this pedal point is located along the circumcircle of the given triangle using GSP.
Circumcenter
In a given triangle ABC, the circumcenter is the center point of a circle that will pass through all three vertices of the triangle. The circumcenter can be located by constructing perpendiculars from the midpoints of each side of the triangle, and finding the intersection point of those perpendiculars.
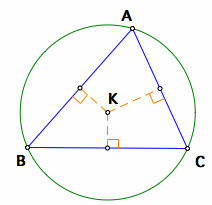
The circumcenter K and the circumcircle of triangle ABC
Pedal Point and Pedal Triangle
Given a triangle ABC, choose the Pedal Point P anywhere along the plane ABC. Construct the perpendiculars from point P to the three sides of triangle ABC, where the sides AB, BC, and AC are extended if necessary, and denote the intersection points R, S, and T. The triangle formed by connecting the three points R, S, and T is called the Pedal Triangle of the Pedal Point P.
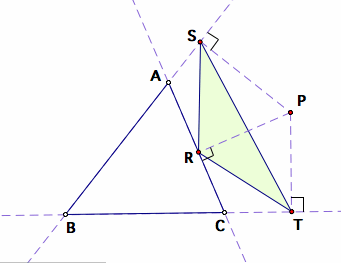
The pedal triangle RST of pedal point P
Pedal Point along the Circle centered at Circumcenter
Let us construct the circumcircle of triangle ABC, and also construct the pedal triangle with the pedal point along the circumcircle. However, we encounter an unexpected outcome. The pedal triangle has degenerated into a line.
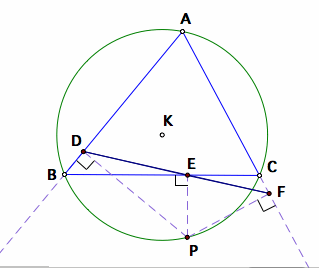
Pedal point located along the circumcircle
It turns out that when the pedal point is along the circumcircle, the three vertices of the pedal triangle are colinear. We therefore call the circumcircle the Simson line, because the circumcircle is the locus of points where the pedal triangle is a straight line.
From the circumcenter K, let us a draw a circle large than the circumcircle, and locate the pedal point on this circle. Then, let us construct the midpoints of RS, ST, RT. (There are denoted by m in the figures below.) Let us trace these midpoints as the pedal point P is moved along the circle.
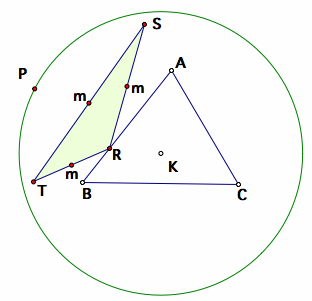
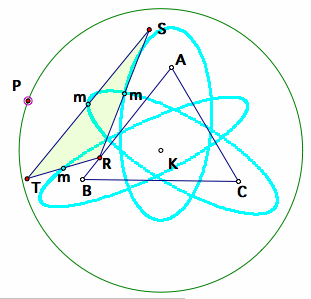
Tracing the midpoints of the Pedal Triangle along the circle located at K
We obtain three ellipse as the locus of these midpoints. Notice that the three ellipse seems to be centered around a angle bisecting line from each vertex of triangle A, B, and C. Let us repeat the trace of the midpoints when the circle is equal to the circumcircle.
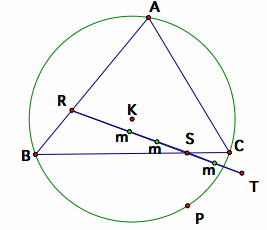
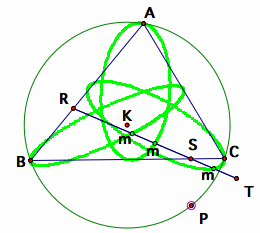
Tracing the midpoints of the Pedal Triangle along the circumcircle
We still obtain three ellipses as the locus of each midpoint. However, in this case, the ellipse seems to be tangent to the triangle at one end. Each ellipse seems to touch one vertex of the triangle and the midpoint of the opposite side.
Now, what if the circle centered at the circumcenter K is smaller than the circumcircle?
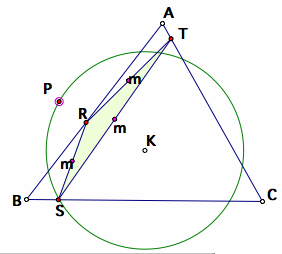
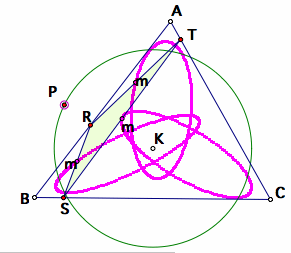
Tracing the midpoints of the Pedal Triangle along the circle located at K
In this case, the ellipse does not reach either the vertex or the other side, but still be centered around a line that seem to be along the bisector or median of each side.
Searching for the Next Cool Firework
Fascinated by the cool traces of these points, I decided to investigate how the traces of the midpoints of the pedal triangle will look for various shapes of triangle ABC. As we have celebrated the Independence Day just a few days ago with fireworks, perhaps some cool shape can bring a new idea for a new firework.
The figures below are meant to be the fireworks to celebrate our Independence.
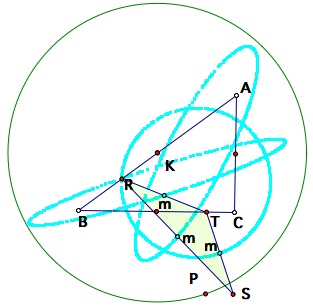
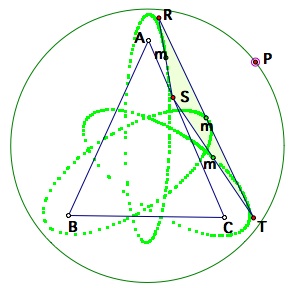
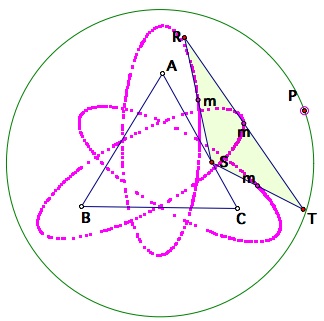
Left: right triangle, Middle: isosceles triangle, Right: equilateral triangle
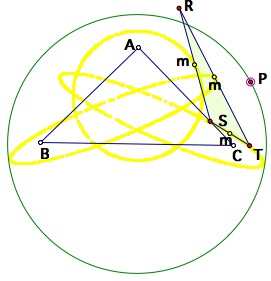
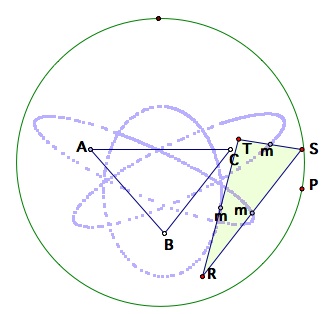
Left: 45-90-45 triangle, Right: just trying to create a cool trace
From the above traces for various shapes of triangle, it becomes clear that there is a relationship between the size of the angle of triangle ABC and the shape of the ellipse. In particular, if the angle of one of the vertex of triangle ABC is 90 degrees, then one of the traces of the midpoints becomes a circle. There is also a relationship between the path of the ellipse and the median of bisecting line of each vertex.