

This is the Extension of the intial exploration of Bouncing Barney, where the problem is redefined in another way. Please click on this link to go back to the original investigation: Return to Bouncing Barney
In this investigation, let us define another path of Barney that is similar to the path described in the original investigation but now Barney is outside the triangle. Let us extend the lines of the triangle and now Barney will start outside the triangle on this extended line. When Barney meets an extended line of the triangle, now instead of bouncing off the line, Barney will go through the line parallel to one of the sides of the triangle.
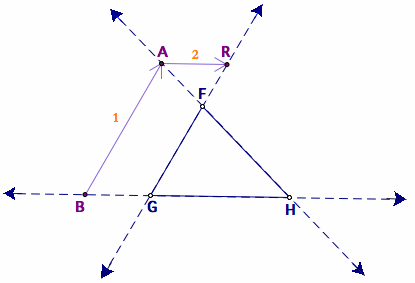
A redefined path of Barney outside the triangle
Let us set Barney's starting point B on the left side of the extended line of segment GH. From point B, he will travel parallel to the side FG until he meets the extended line of segment FH. At this intersection, Barney will now go through the line segment, and change direction such that his new path will be parallel to the segment GH. When he meets another extended line segment at point R, he will again redirect.
Here is a GSP file that traces the path of Barney in this manner: CLICK HERE. (The legs of Barney will change when you adjust the size of the given triangle...)
In this newly defined setting, we see that Barney still comes back to the original starting point!
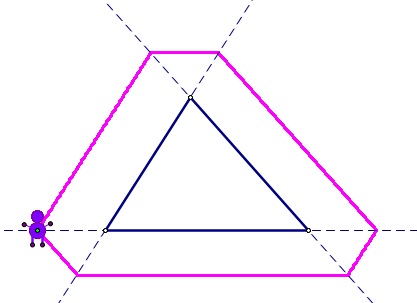
Barney returns back to his original starting point
Let us prove that Barney will return back to his starting point.

The green-colored segments are all equal in length
Consider quadrilateral BARG. Since the line BA is parallel to FG and line AR is parallel to BG, by definition of Barney's path, it follows that quadrilateral BARG is a parallelogram. As the opposing sides of the parallelogram are equal in length,
![]()
Similarly, quadrilateral ARNH is also a parallelogram because AR is parallel to HN and AH is parallel to RN by definition of Barney's path. Therefore, AR is equal to HN. That is,
![]()
Now let us draw a parallel line of NE at point H until the line intersects with the line segment YE. As the line segemnts HQ and NE, and HN and QE are parallel, the quadrilateral QENH is a parallelogram. Therefore, HN = QE. That is,
![]()
Now, quadrilateral GHQY is also a parallelogram, because HQ is parallel to NE which is parallel to GY, and GH is parallel to YQ by definition. Hence,
![]()
Now let us consider when Barney is at point Y, and is about to redirect through the line at Y. By definition, he will redirect such that his path is parallel to side FH of the triangle. If we compare the lengths BH and YE, there are equal because from the two previous equations we know
![]()
Therefore, because length BH and YE are equal and parallel to one another, a parallel line to the side FE at point Y must go through the initial starting point B.
We can create a triangle such as in the figure below to note the difference in the distances. If we slide segment BY toward the direction up and right until point Y is located at point R, slide the segment NE to the up and left until point E is at point A, and slide YE upward and AR downward and right, we can create this triangle. The total length of this new redefined path is equal to the perimeter of this triangle.
Let us say the starting point is chosen such that BG is equal to length 'a'. If we label the triangle BGY as a, b, c, then the total length of Barney's trip will be equal to the perimeter of the original triangle FGH plus 2 times the perimeter of triangle BGY. This can be reasoned by noting that each side of the orange triangle is equal to one of the original triangle's side plus two times the segment of BGY that is parallel to that side. (This can be shown by constructing parallel lines.)
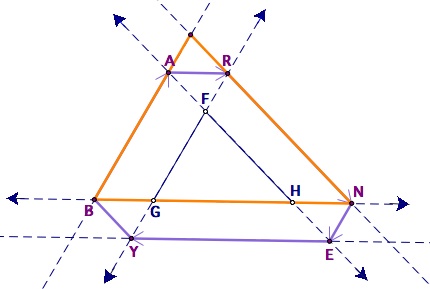
The orange triangle is equal in length to Barney's path
Return to First Investigatoin of Bouncing Barney